Система двух дифференциальных уравнений с рациональными правыми частями третьей степени

Рассмотрим автономную систему дифференциальных уравнений

(2.1)

где

Исключая 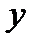и из системы (2.1) получим уравнение для

(2.2)

где

(2.3)

Необходимо, чтобы уравнение (2.2) было полиномом по не выше второй степени. Рассмотрим случаи и , где .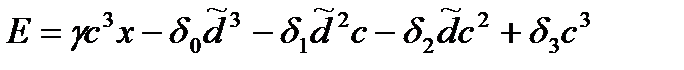

Если ,тогда требуем, чтобы . Т.к. следует . Отсюда (2.4)

Если , значит 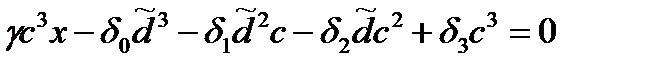(2.5)

Пусть , тогда . Условие невозможно, т.к. и .

Пусть , тогда также должно выполняться условие Данное условие невозможно, т.к. и .

Пусть , тогда

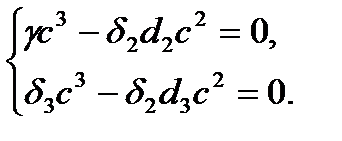, отсюда (2.6)

Из системы (2.6) получим условия

(2.7)

В силу симметрии системы (2.1) получим условия

(2.8)

. (2.9)

Рассмотрим возможные случаи. Первый случай, когда одновременно выполняются условия (2.4) и (2.8). Второй случай, когда выполняются условия (2.7) и (2.9). Случаи (2.7) и (2.8) не могут одновременно выполняться, как и случаи (2.4) и (2.9).

2.1. Случай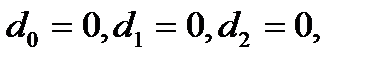

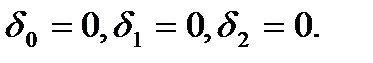
Из системы (2.1) получим систему

(2.10)

(2.10’)

где

Введем в систему (2.10’) параметр 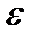по формулам:

Тогда система примет вид

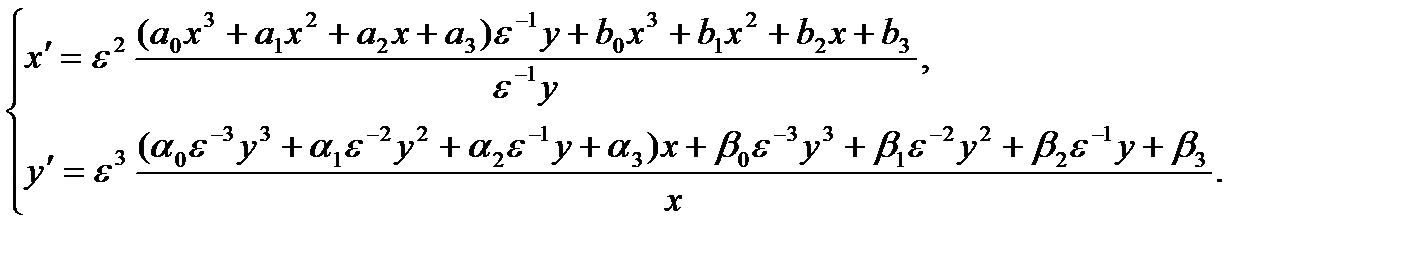
отсюда

При получим систему

(2.11)

Для отсутствия у системы (2.11) подвижных критических точек необходимо, чтобы . В силу симметрии получим .

Учитывая эти условия система (2.10’) примет вид

(2.12)

Исключая и из системы (2.12) получим уравнение для

(2.13)

где

Уравнения вида (2.13) со свойством Пенлеве содержатся в работах Пенлеве и Гамбье.

Теорема 2.1. Для того чтобы система (2.10) имела свойство Пенлеве необходимо и достаточно, чтобы она имела вид (2.12) и решения уравнения (2.13) не имели подвижных критических особых точек.

2.2 Случай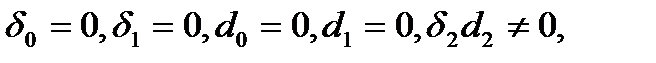

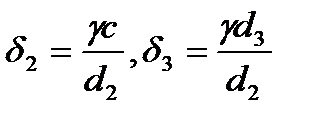
Система (2.1) примет вид

(2.14)

Сделаем замену 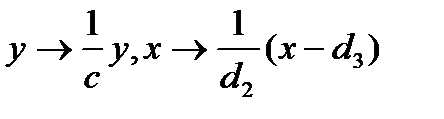, тогда система примет вид

(2.15)

где

Введем в систему (2.15) параметр по формулам

Из системы (2.15) получим систему

(2.16)

(2.16’)

Если , то решения системы (2.15) однозначны, только если , отсюда получаем

(2.17)

Получим условия , в силу симметрии также получим 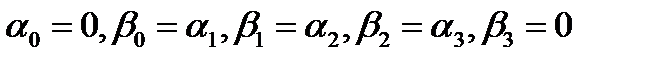(2.18)

С учетом этих условий система (2.15) примет вид

(2.19)

(2.19’)

Получили систему уравнений Риккати. Система не имеет подвижных критических особых точек.

Теорема 2.2. Для того чтобы система (2.1) при 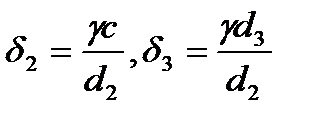имела свойство Пенлеве необходимо и достаточно, чтобы выполнялись соотношения (2.18).

Если , тогда решения системы (2.15) однозначны только если , отсюда

(2.20)

Получим необходимые условия для отсутствия в системе (2.15) подвижных особых критических точек:

(2.21)

С учетом условий (2.21) система (2.15) примет вид

(2.22)

Исключая и из системы (2.28) получим уравнение для

(2.23)

Рассмотрим два случая

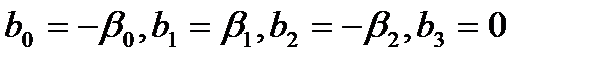(2.24)

. (2.25)

2.2.1. Случай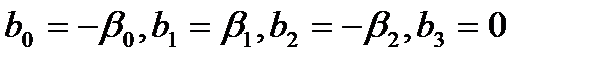

Система (2.22) примет вид

(2.26)

Исключая и из системы (2.26) получим уравнение для

(2.27)

Выполнив замену получим 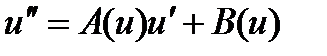(2.27’)

Уравнения вида (2.27’) со свойством Пенлеве содержатся в работах Пенлеве и Гамбье.

Теорема 2.3. Для того чтобы система (2.22) имела свойство Пенлеве необходимо и достаточно, чтобы она имела вид (2.26) и решения уравнения (2.27) не имели подвижных критических особых точек.

2.2.2. Случай

Система (2.22) примет вид

(2.28)

Исключая и из системы (2.28) получим уравнение для

(2.29)

Выполнив замену из уравнения (2.29) получим уравнение

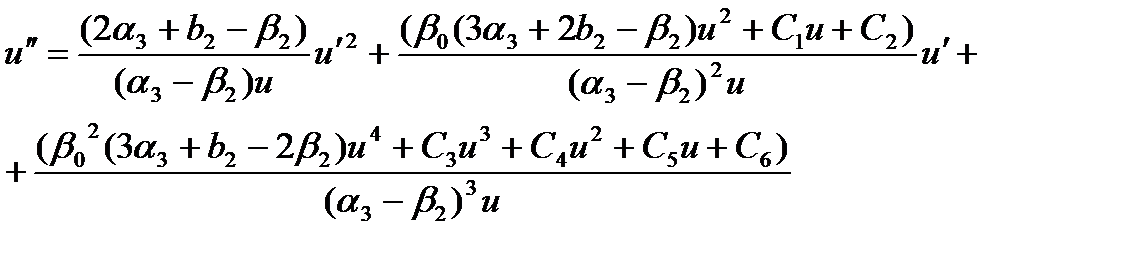(2.30)

где , .

Для того чтобы решения системы (2.28) не имели подвижных критических точек необходимо, чтобы выполнялось условие

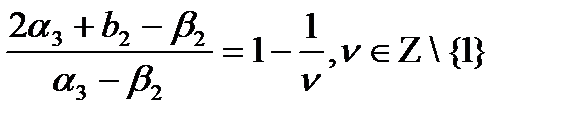(2.31)

Уравнения вида (2.38) со свойством Пенлеве содержатся в работах Пенлеве и Гамбье.

Теорема 2.4. Для того чтобы система (2.22) имела свойство Пенлеве необходимо и достаточно, чтобы она имела вид (2.28) выполнялось условие (2.31) и решения уравнения (2.29) не имели подвижных критических особых точек.

Date: 2016-06-06; view: 865; Нарушение авторских прав