Десятичные двоично-кодированные системы

Иногда в ЭВМ используются десятичные системы счисления. Их выгодно использовать тогда, когда объем исходных данных для обработки на ЭВМ – велик, сама обработка производится по относительно несложным программам. На этом происходит значительная экономия времени, которая вытекает из того, что не нужно делать перевод из десятичной в двоичную систему и обратно.

Как правило, в состав оборудования таких ЭВМ вводится АУ, работающее с числами в десятичной системе счисления. Поскольку в качестве основного запоминающего элемента используется триггер-ячейка с двумя устойчивыми состояниями, то каждая десятичная цифра кодируется совокупностью двоичных символов.

Перевод чисел из десятичной системы в десятичную двоично-кодированную выполняется исключительно просто, поразрядно и одновременно по всей сетке:

Аналогично, выполняется и обратный перевод:

Существует большое разнообразие десятичных двоично-кодированных систем. Это многообразие вытекает из избыточности двоичного кода, при котором из 16 возможных комбинаций в каждом разряде используется по прямому информационному назначению лишь 10.

Наиболее широкое применение находят системы кодирования 8421 и 8421⁺³ (код Штибитца).

Система 8421 – неудобна тем, что при выполнении операции вычитания нет прямого перехода от цифры каждого разряда к дополнительному коду.

0000 - 0

0001 - 1

0010 - 2

0011 - 3

0100 - 4

0101 - 5

0110 - 6

0111 - 7

1000 - 8

1001 - 9

В то же время эта система обладает свойством аддитивности, поскольку результаты операции сложения над числами в десятичной системе и над их изображением в системе 8421 – совпадают.

Система 8421⁺³ - более интересна, т.к. она обладает свойством самодополнения. Видно, что дополнение до 9 можно получить, применяя операцию поразрядного инвертирования кода.

0011 – 0

0100 – 1

0101 – 2

0110 – 3

0111 – 4

1000 – 5

1001 – 6

1010 – 7

1011 – 8

1100 – 9

Всего существует А₁₆¹⁰ = 2,9•10¹⁰ вариантов 10-ых двоично-кодированных систем.

10. Лекция: Структура однопрограммной ЭВМ
Страницы: 1 | 2 | вопросы |»	| учебники | для печати и PDA | ZIP
Если Вы заметили ошибку - сообщите нам, или выделите ее и нажмите Ctrl+Enter
Рассматриваются классические основы построения ЭВМ (машина Тьюринга, элемент и автомат Неймана), принципы Неймана построения ЭВМ, структура классической ЭВМ.
Классические основы построения ЭВМ Основы построения электронных вычислительных машин в их современном понимании были заложены в 30-е – 40-е годы прошлого века видными учеными: английским математиком Аланом Тьюрингом и американцем венгерского происхождения Джоном (Яношем) Нейманом. Машина Тьюринга В 1936 году А. Тьюринг сформулировал понятие абстрактной вычислительной машины. Одновременно с ним, хотя и не в столь явной форме, это же сделал Э. Пост (США). Хотя машина Тьюринга (МТ) не стала реально действующим устройством, она до настоящего времени постоянно используется в качестве основной модели для выяснения сущности таких понятий, как "вычислительный процесс", "алгоритм", а также для выяснения связи между алгоритмом и вычислительными машинами [11]. Основные положения машины Тьюринга 1. Машина Тьюринга (рис.10.1) имеет конечное число знаков si, образующих внешний алфавит, в котором кодируются сведения, подаваемые в МТ, а также вырабатываемые в ней. Среди знаков имеется пустой знак (s1), посылка которого в какую-либо ячейку стирает находившийся в ней знак и оставляет ее пустой. 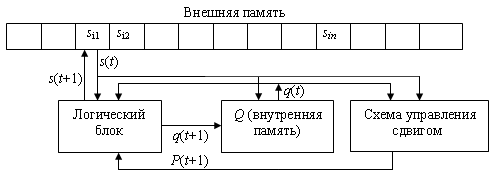Рис. 10.1. Структура машины Тьюринга В зависимости от поданной начальной информации (содержащихся на ленте внешней памяти знаков) возможны два случая: после конечного числа тактов машина останавливается (имея информацию β), подавая сигнал об остановке. В этом случае МТ применима к информации a и перерабатывает ее в информацию β; остановка никогда не наступает. В этом случае МТ не применима к начальной информации . 2. В каждый момент обозревается лишь одна ячейка ленты (памяти). Переход может осуществляться лишь к соседней ячейке (R – вправо, L–влево, N– нет перехода (остаться)). Переход к произвольной ячейке производится путем последовательного перебора всех ячеек, разделяющих текущую и необходимую ячейки. На каждом отдельном такте t команда предписывает только замену единственного знака si, хранящегося в обозреваемой ячейке, каким-либо другим знаком sj. 3. Логический блок МТ имеет конечное число состояний {qi} i=1..m. Знаки R, L, N, q1,..,qmобразуют внутренний алфавит машины. Переработанный знак sj, записываемый в просматриваемую ячейку, состояние, которое примет машина Тьюринга в следующем такте q(t+1) и выполняемая в данном такте операция перехода к следующей ячейке P(t+1) являются функцией анализируемого в данном такте символа и текущего состояния машины si и q(t): si(t+1)=f1(si,q(t));q(t+1)=f2(si,q(t));P(t+1)=f3(si,q(t)). Программа для МТ определяется тройкой {si, P, q}t. Пример записи программы вычисления логической функции "неравнозначность" для машины Тьюринга представлен ниже. Символ (si) Состояние q1 q2 q3 q4   0, R, q1 0, N, q4 1, N, q4 0, N, q4   1, R, q3 1, N, q4 0, N, q4 1, N, q4 Перед началом работы машина Тьюринга находится в состоянии q1 считывания первого операнда. Данная МТ применима к исходной информации. Останов – состояние q4. Значение si в ячейке y не меняется (сохраняется результат). Если программа для МТ будет определена таблицей переходов Символ (si) Состояние q1 q2 q3 q4   0, R, q2 0, N, q4 1, N, q4 1, N, q4   1, R, q3 1, N, q4 0, N, q4 0, N, q4 то данная МТ будет не применима к исходной информации, поскольку в состоянии q4 значение si в ячейке y постоянно меняется на противоположное.

Автомат Неймана

По принципу обработки информации вычислительное устройство, предложенное Нейманом (автомат Неймана – АН), существенно отличается от машины Тьюринга.

Важная особенность машины Тьюринга – преобразование информации на каждом такте происходит лишь в одной ячейке, остальные дожидаются посещения головки, хотя часто имеется возможность работать параллельно.

Простейшее решение – использование нескольких машин Тьюринга с общей для них внешней памятью (лентой) – не всегда допустимо из-за возможных конфликтов при обращении к одной и той же ячейке памяти.

В автомате Неймана число одновременно обрабатываемых ячеек может неограниченно расти, оставаясь в каждый момент конечным.

Элемент Неймана (ЭН) – это устройство, которое на каждом такте пребывает в одном из конечного числа состояний r_i R, образующих его алфавит. ЭН имеет два входных канала: левый и правый; по каждому из них на такте t также поступает по одному состоянию из R (рис. 2).

Рис. 10.2. Элемент Неймана

Элемент реализует функцию z_t+1= (r_i, r_j, r_m)_t, то есть в такте t+1 переходит в состояние z, определяемое его состоянием в текущий момент времени и значениями, поступившими по входным каналам.

Состояния элементов Неймана в момент времени t определяют конфигурацию автомата Неймана (рис. 3) в момент t: K(t).

Рис. 10.3. Структура автомата Неймана

Функционирование АН – это переход от состояния К(t) к состояниям K(t+1), K(t+2)...

За один такт свое состояние может менять большое число элементов Неймана, что фактически приводит к параллельной обработке информации.