Системы координат в трехмерном пространстве. Афинные преобразования. Свойства афинных преобразований. Общий вид афинных преобразований. Обратное преобразование

Система координат (СК) – совокупность базисных (линейно-независимых) векторов и единиц измерения расстояния вдоль этих векторов (e1, e2, …, en).

Если базисные вектора нормированы (единичной длины) и взаимно ортогональны, то такая система координат называется декартовой (ДСК).

Мировая система координат (МСК) – xyz – содержит точку отсчёта (начало координат) и линейно независимый базис, благодаря которым становится возможным цифровое описание геометрических свойств любого графического объекта в абсолютных еденицах.

Экранная система координат (ЭСК) - x_эy_эz_э . В ней задаётся положение проекций геометрических объектов на экране дисплея. Проекция точки в ЭСК имеет координату
z_э = 0. Тем не менее, не следует отбрасывать эту координату, поскольку МСК и ЭСК часто выбираются совпадающими, а, вектор проекции [x_э ,y_э, 0] может участвовать в преобразованиях, где нужны не две, а три координаты.

Система координат сцены (СКС) – x_сy_сz_с – описывает положение всех объектов сцены – некоторые части мирового пространства с собственным началом отсчёта и базисом, которые используются для описания положения объектов независимо от МСК.

Объектная система координат (ОСК) – x_оy_оz_о – связана с конкретным объектом и совершает с ним все движения СКС или МСК.

Правая ДСК – оси ориентированы так, что вращение ортов происходит в положительном направлении (против часовой стрелки с точки зрения наблюдателя, находящегося на конце третьего свободного орта):

Левая ДСК – оси ориентированы так, что вращение ортов происходит в отрицательном направлении.

В двумерном пространстве (R²) наиболее распространены декартова СК (x, y) и полярная СК (r, φ) (r – радиус-вектор точки, φ – угол поворота).

Соотношение между ДСК и ПСК:

x = r*cos(φ) r = sqrt(x²+y²)

y = r*sin(φ) tg(φ) = y/x

В трёхмерном пространстве (R³):

- Ортогональная декартова СК (x, y, z);

- Цилиндрическая СК (ρ, y, φ);

- Сферическая СК (r, φ, ω).

Соотношение между декартовой СК и цилиндрической СК:

x = ρ *sin(φ) ρ = sqrt(x²+z²)

y = y y = y

z = ρ *sin(φ) tg(φ) = x/z

Соотношение между декартовой СК и сферической СК:

x = r *sin(φ)*sin(ω) r = sqrt(x²+ y²+z²)

y = r *cos(ω) tg(φ) = x/z

z = r *cos(φ)*sin(ω) tg(ω) = sqrt(x²+ y²)/y

Соотношение между цилиндрической СК и сферической СК:

ρ = r*sin(ω) r = sqrt(ρ²+y²)

y = r*cos(ω) tq(ω) = ρ/y

φ = φ φ = φ

Аффинным называется преобразование, обладающее следующими свойствами:

- Любое аффинное преобразование может быть представлено как последовательность операций из числа простейших: сдвиг, растяжение/сжатие, поворот;

- Сохраняются прямые линии, параллельность прямых, соотношение длин отрезков, лежащих на одной прямой, и отношение площадей фигур.

Аффинные преобразования координат на плоскости:

(x, y) – двумерная система координат;

(X, Y) – координаты старой СК в новой СК.

Общий вид аффинного преобразования:

X = A*x + B*y + C

Y = D*x + E*y + F

A, B, C, D, E, F – константы.

Обратное преобразование также является аффинным:

x = A`*X+B`*Y+C`

y = D`*X+E`*Y+F`

Простейшие аффинные преобразования системы координат.

1. Параллельный сдвиг координат:

обратное преобразование:

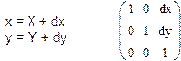
1. Растяжение/сжатие осей:

обратное преобразование:

Коэффициенты могут быть отрицательными. Например, при kx = -1 получаем зеркальное отображение относительно оси y.

1. Поворот системы координат (x, y) на угол α:

обратное преобразование – поворот системы (X, Y) на угол – α

Аффинные преобразования объектов на плоскости.

X = A*x + B*y + C

Y = D*x + E*y + F

x, y – старые координаты, X, Y – новые координаты точки.

1. Сдвиг:

обратное преобразование:

2. Масштабирование объекта:

обратное преобразование:

1. Поворот вокруг центра координат:

обратное преобразование:

Преимуществом матричной записи аффинного преобразования заключается в том, что любое преобразование, являющееся последовательностью преобразований, можно записать при помощи одной матрицы.

Пусть мы выполняем подряд три преобразования, заданных матрицами M₁, M₂, M₃. Эти три преобразования можно записать одной матрицей М = M₃* M₂* M₁ .

Обратное преобразование находится при помощи обращения матрицы прямого преобразования. Если определитель исходной матрицы равен 0, то преобразование обратного не имеет и называется необратимым.

4. Основные функции базовой графики. Точки, линии, полигоны. Методы заполнения площади. Видовые операции. Геометрические преобразования графических объектов. Графические библиотеки в языках программирования.

В данном вопросе сосредоточим внимание на двухмерной графике. Существует достаточно большое количество различных библиотек, реализующих базовую графическую функциональность. Следует выделить основные функции, предоставляемые этими библиотеками:

1) Инициализация графического режима. Существует большое количество графических режимов, отличающихся разрешающей способностью и способом представления цвета (разная разрядность, палитровые режимы). Для начала работы с графической библиотекой обычно необходимо произвести её инициализацию.

2) Также достаточно важной часть функциональности является возможность выводить текст. Причём перед его выводом может потребоваться ряд настроек: выбор шрифта для вывода, размеры шрифта, его цвет, установка атрибута прозрачности, выбор фонового цвета заливки и т.д. Для вывода обычно указывается позиция левого нижнего угла строки и непосредственно строка, но возможны и более продвинутые варианты, как например задание окна для вывода, внутри которого можно осуществлять форматирование текста.

3) Работа с битмапами (растровыми изображениями). Практически все библиотеки предоставляют ту или иную функциональность по загрузке, сохранению и выводу растрового изображения.

4) Работа с примитивами. В качестве основных базовых примитивов используются точки, линии, полигоны, окружности, эллипсы и т.д.

- Для вывода точки обычно используют указание её позиции на экране, а также цвет.

- Под линиями обычно понимают прямые линии, для задачи которых достаточно двух крайних точек. Также для линии можно задать ширину, шаблон вывода (пунктирная, сплошная, штрихпунктирная…) и цвет. Обычно библиотеки предоставляют возможность рисовать цепочку прямых линий: каждая последующая прямая линия использует в качестве исходных данных конечную вершину предыдущей прямой и заданную пользователем вершину.

- Помимо прямых линий библиотека может также предоставлять функции для работы с дугами, сплайнами и кривыми Безье. Для того, чтобы нарисовать сплайн или кривую Безье, достаточно задать последовательность опорных точек. Для отрисовки дуги достаточно указать центр, радиус, а также начальный и конечный угол.

- Под полигоном понимается многоугольник. Поскольку он состоит из прямых линий, то атрибуты его вывода настраиваются аналогично. Задача полигона осуществляется последовательным перечислением его вершин, результирующий полигон получается в результате последовательного соединения вершин и замыкания отрезком по первой и последней вершине.

5) Заливка. Под заливкой понимается заполнение площади, ограниченной каким-либо контуром. Основными атрибутами заливки являются цвет и шаблон заполнения (сплошной, сетка…). Для заливки используют два основных подхода: заливка путём указания точки заполнения, а также заливка на основе геометрического описания контура. В общем виде алгоритм закрашивания произвольного контура, который уже нарисован в растре, предполагает выполнение следующих действий:

- находим пиксель внутри контура фигуры;

- цвет этого пикселя изменяем на нужный цвет заполнения;

- производим анализ соседних пикселов;

- если цвет некоторого соседнего пикселя не равен цвету границы контура или цвету заполнения, то цвет этого пикселя изменяется на цвет заполнения;

- анализируем цвет пикселов, соседних с предыдущим; и так далее, до тех пор, пока внутри контура все пиксели не перекрасятся в цвет заполнения.

Пиксели контура – это граница, за которую нельзя выходить в ходе последовательного перебора всех соседних пикселов. Соседними могут считаться только четыре пикселя (четырёхсвязность) или восемь (восьмисвязность). Не всякий контур может служить границей закрашивания.

Простейший алгоритм закрашивания:

1. Определить x0, y0 (точка заполнения).

2. Выполнить процедуру Закрасить (x0, y0)

Процедура Закрасить(x, y) описана в виде:

Если цвет пикселя(x, y) не равен цвету границы, то

устновить для пикселя(x, y) цвет заполнения;

закрасить(x+1, y);

закрасить(x-1, y);

закрасить(x, y+1);

закрасить(x, y-1).

Очевидно, что это рекурсивная процедура. Подобная запись упрощает понимание, но замедляет работу алгоритма.

Волновой алгоритм закрашивания. Идея волнового алгоритма заключается в том, что пиксели закраски, порождённые на предыдущей итерации, являются источниками закраски для последующей итерации. Таким образом, на каждой итерации мы наблюдаем волновое распространение пикселов от исходной точки. Данный алгоритм практически полностью повторяет простейший алгоритм, но в отличие от него является итерационным, а не рекурсивным, поэтому работает несколько быстрее.

Алгоритм закрашивания линиями получил широкое распространение в компьютерной графике. От приведённого ранее простейшего рекурсивного алгоритма он отличается тем, что на каждом шаге закрашивания рисуется горизонтальная линия, которая размещается между пикселями контура. Алгоритм рекурсивный, но поскольку вызов функции осуществляется для лини, а не для каждого отдельного пикселя, то количество вложенных вызовов уменьшается пропорционально длине линии. Это снижает нагрузку на стековую память компьютера.

Заполнение прямоугольника. Если прямоугольник задан координатами противоположных углов, например, левого верхнего (x1, y1) и правого нижнего (x2, y2), тогда алгоритм может заключаться в последовательном рисовании горизонтальных линий заданного цвета.

Заполнение полигона. Один из наиболее популярных алгоритмов заполнения полигона заключается в закрашивании фигуры отрезками прямых горизонтальных линий. Алгоритм представляет собою цикл вдоль оси y, в ходе этого цикла выполняется поиск точек сечения линии контура с соответствующими горизонталями. Этот алгоритм получил название XY:

1. Найти min{yi} и max{yi} среди всех вершин Pi.
2. Выполнить цикл по y от y=ymin до y = ymax:
3. Найти точки пересечения всех отрезков контура с горизонталью y;
4. Координаты xj точек сечения записать в массив;
5. Отсортировать массив {xj} по возрастанию x;
6. Вывести горизонтальные отрезки с координатами

(x₀, y)-(x₁, y)

(x₂, y)-(x₃, y)

.. (x_2k, y) – (x_2k+1, y)

6) Видовые операции. Многие современные библиотеки используют понятие окна вывода (Viewport). Обычно он задаётся в виде прямоугольной области экрана указанием точки левого верхнего угла, а также ширины и высоты области.

Viewport позволяет:

- делать отсечение вывода по заданной области экрана;

- вписывать весь вывод в заданную область экрана (с масштабированием);

- осуществлять различные операции над выводимым изображением, например поворот вида.

7) Геометрические преобразования графических объектов. Для большинства графических объектов преобразование можно задать матрицей, изменяющей положение всех точек графического объекта.

x, y – старые координаты, X, Y – новые координаты точки.

1. Сдвиг:

обратное преобразование:

2. Масштабирование объекта:

обратное преобразование:

1. Поворот вокруг центра координат:

обратное преобразование:

Существует достаточно богатое многообразие графических библиотек по работе с двумерной графикой и по работе с трёхмерной графикой.

2-х мерная графика:

- Borland Graphics Interface (BGI), встроена в среды разработки Turbo Pascal и Turbo C, расcчитана на использование в ОС MS DOS.

- Graphic Device Interface (GDI), библиотека для работы с графикой под управлением ОС Windows, является достаточно медленной и практически не использует аппаратные возможности. Предназначена для формирования простейших изображений, в основном для оформления пользовательского интерфейса.

- DirectDraw – компонента DirectX, отвечающая за работу с двумерной графикой, достаточно неудобна, но предоставляет полное аппаратное ускорение, используется в основном для написания видеоплееров и мультимедийных приложений.

- OpenGL – имеет своей составляющей библиотеку для работы с 2-х мерной графикой, также использует аппаратное ускорение.

3-x мерная графика:

- Direct3D – компонента DirectX, предоставляет полное аппаратное ускорение при работе с трёхмерной графикой, на сегодняшний момент является самой популярной библиотекой для разработки мультимедийных приложений под управлением ОС Windows.

- OpenGL – также использует аппаратные возможности. В отличие от Direct3D является кроссплатформенным стандартом и не завязан на продукцию Microsoft. Является полностью бесплатной и независимой библиотекой.

* В последних версиях DirectX (начиная с 9.0), пропало разделение графической подсистемы на Direct3D и DirectDraw, теперь обобщённая компонента называется Direct Graphics.

Date: 2016-05-25; view: 992; Нарушение авторских прав