Статистикалары туралы ұғым

Ұқсас объектілердегі үлкен сандарды зерттеу үшін (атомдардағы, молекулалардағы) молекулалық физикада қолданылатын классикалық статистикалық әдіске сәйкес, айнымайтын бірдей кванттық бөлшектердің үлкен сандарынан тұратын кванттық механиканың заңдарына бағынатын кванттық жүйелер үшін кванттық статистикасының әдістері қолданылады.

Классикалық жүйелердің молекулалық физикасында берілген температурасы кезіндегі сыртқы потненциалдық өрістегі идеалды газдардағы энергиялардың таралуы Больцман таралуымен бейнеленетінін ескертейік:

мұндағы -Больцман тұрақтысы.

Кванттық статистикада сондай-ақ, бірдей бөлшектердің жиынынан құралатын жүйенің берілген кванттық күйін толтырудың деңгейін көрсететін толтыру саны деп аталатын 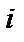кванттық сандар жиынымен берілген кванттық күйдің негізгі сипаттамасы болып табылатын квазибөлшектердің идеалды газының моделі қолданылады.

Бозондар болып құрылған жүйелер үшін, толтыру сандары кез-келген толық мәнді қабылдай алады: 0,1,2,...

Фермиондар болып құрылған жүйелер үшін, толтыру сандары тек 2 мәнді ғана қабылдай алады: бос күйлер үшін 0, бос емес күйлер үшін 1. Барлық сандардың толтырылу қосындысы жүйелердегі бөлшектердің санына тең болуы керек. Кванттық статистикада берілген кванттық күйдегі бөлшектердің орташа санын есептеуге, яғни 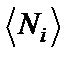толтырудың орташа санын анықтауға болады.

Бозондардан тұратын идеалды газ – бозе-газ - Бозе-Эйнштейн кванттық статистикасын бейнелейді.

Бозе-Эйнштейн таралуы - бозе-газдағы энергетикалық күй бойынша бөлшектердің таралуын білдіретін заң: статистикалық тепе-теңдік кезінде және 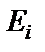энергиясы бар күйдегі бөлшектердің орташа сандарының қатынасы жоқ кезінде:

.

мұндағы -Больцман тұрақтысы, - термодинамикалық (абсолюттік) температура, 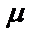- химиялық потенциал –барлық басқа бөлшектердің ішкі энергиясы (энтропия, көлем және т.б) тәуелді болатын шартта жүйедегі бөлшектер санының өзгерісі кезіндегі жүйедегі бөлшектердің ішкі энергиясының (жалпы айтқанда, басқа термодинамикалық потенциалдар) өзгерісін анықтайтын күйдің термодинамикалық функциясы.

Фермиондардан тұратын идеалды газ – ферми-газ - Ферми-Дирактың кванттық статистикасын бейнелейді.

Ферми-Дирак таралуы -ферми-газдағы энергетикалық күй бойынша бөлшектердің таралуын білдіретін заң: статистикалық тепе-теңдік кезінде және 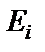энергиясы бар күйдегі бөлшектердің орташа сандарының қатынасы жоқ кезінде:

Жоғары температура кезінде, болғанда екеуі де

Бозе-Эйнштейн және Ферми-Дирак таралуы да Максвелл-Больцманның классикалық таралуына ауысады:

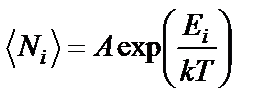, мұндағы . Сондықтан, жоғары температура кезінде «кванттық» газдың екеуі де өздерін классикалық газ тәрізді көрсетеді.

Паули принципі.

Электрондар (фермиондар) жүйесі табиғатта тек антисиметриялық толқындық функциямен бейнеленетін күйде ғана кездеседі.

Осыдан, бір жүйеге кіретін екі бірдей электрондардың (фермиондардың) бірдей күйде тұруы мүмкін еместігі шығады (болмаса орын ауыстыру кезінде толқындық функция жұп болған еді).

(Бірдей күйдегі бозондарда кез-келген сандардың болуы мүмкін еместігі көрсетіледі).

Паули принципінің басқаша тұжырымдамасы: бір және сол атомның өзінде бірдей 4 кванттық сандар жиынынан тұратын бір электроннан артық электрондардың болуы мүмкін емес.

Date: 2016-05-25; view: 1294; Нарушение авторских прав