Электр және магнетизм бөлімі бойынша мысал есептер

Есеп 1. Ұзындығы 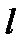= 50 см жұқа стержень(сурет) біртекті q=5 мкКл заряд алып келеді. b=15см стерженнен h=30 мм арақашықтықта тұрған А нүктесінің электр өрісінің кернеулігін табу керек.

Берілгені: q=5 мкКл; l=50 см; в=15 см

Табу керек: Е_А-?

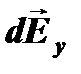
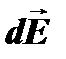
A α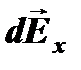

α

α₁ α₂

r

dr

α

dl l в

Сурет

Шешуі: Есептің шарты бойынша стерженнің заряды нүктелік емес, стерженнің бойымен тараған заряд болып есептеледі. Бірақ, егерде стерженнің қандай да бір кішкентай dl ұзындығын алсақ, онда зарядты dq= 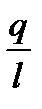dl нүктелік деп айтуға болады.

А нүктесінде пайда болатын d 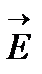кернеулігін келесі теңдеуден анықтаймыз:

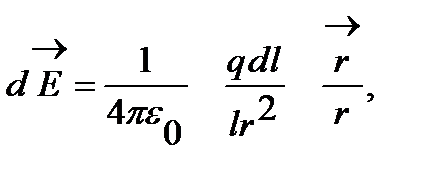(1)

мұндағы r – белгіленген элементтен А нүктесіне дейінгі ара қашықтық, суреттен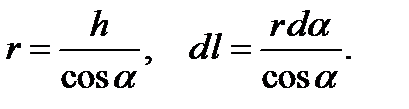

Осыларды (1) теңдеуге қоя отырып

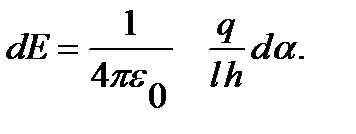(2)

d – вектор екенін ескере отырып, интегралдау алдында екі құраушыға бөлеміз: стерженнің ұзындығына dE_y – перпендикуляр және dE_x – параллель. Суреттен, dE_y=dE cos ,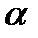

dE_x=dE sin .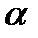

(2) теңдеудегі dE мәнін осы формулаларға қойсақ, онда:

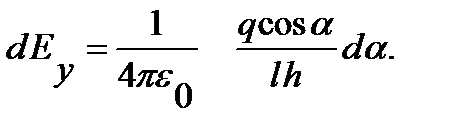
Электр өрісінің суперпозиция принципіне сәйкес, А нүктесінде зарядталған стерженнің тудыратын электр өрісінің кернеулігін интегралдау арқылы табамыз:

(3)

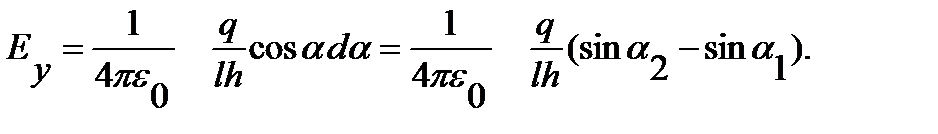(4)

векторының модулін Пифагор теоремасынан табамыз.

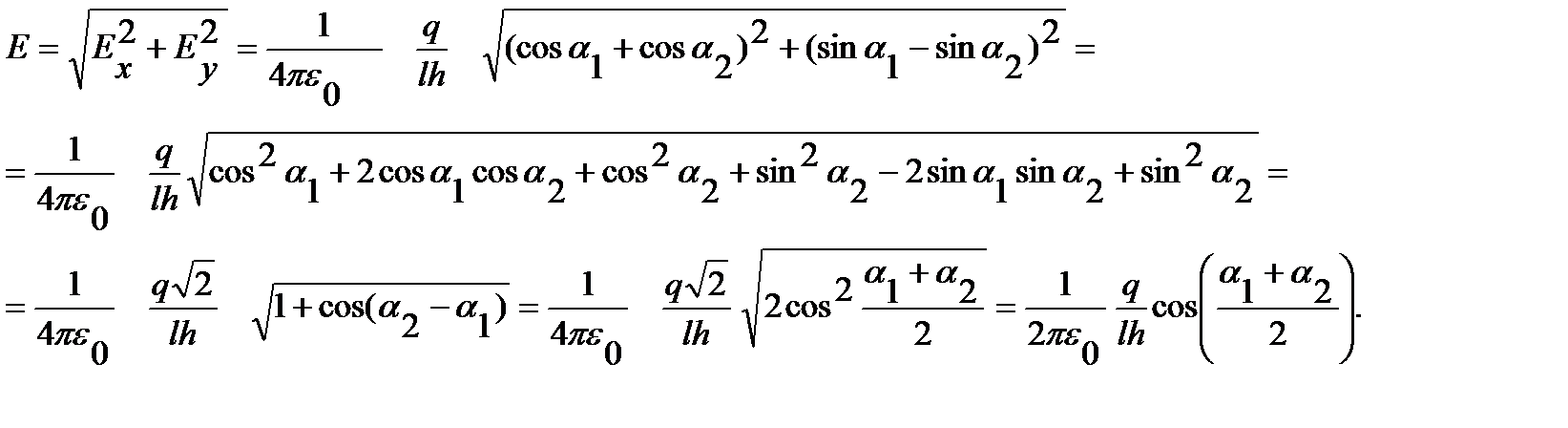
Теңдеудің оң жағы кернеуліктің бірлігін беретінін тексеріп алайық:

.

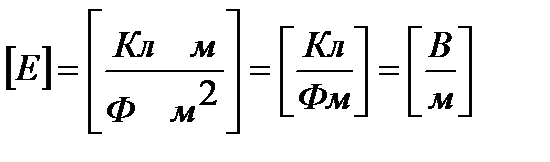Осы шамаларды СИ жүйесінде белгілеп алайық

.

Сан мәндерін қоя отырып, есептің шешімін табайық. Суреттен,

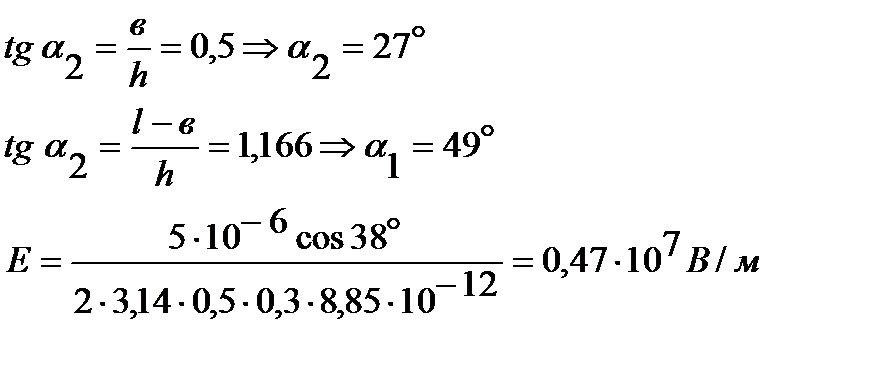
А нүктесіндегі өрісінің кернеулігі 0,47·10⁷ В/м-ға тең болады.

Жауабы: .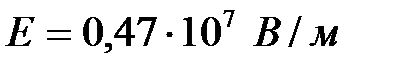

Есеп 2. Бір – бірінен l=5 см қашықтықта орналасқан екі ұзын өткізгіш бойларынан бір бағытта I=5A тоқ жүреді. Әр өткізгіштен r=3 см қашықтықта орналасқан нүктедегі магнит өрісінің индукциясын анықтау керек.

Шешуі: А нүктесіндегі магнит өрісінің индукциясы суперпозиция принципі бойынша әрбір тоқтың осы нүктеде тудыратын өрістер индукцияларының векторлық қосындысына тең (1-сурет), яғни B=B₁+B₂. B₁ және B₂ векторларының бағытын бұранда ережесі бойынша анықтаймыз. Ал олардың шамаларын түзу тоқ өрісінің магнит индукциясы формулаларымен табуға болады: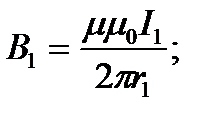

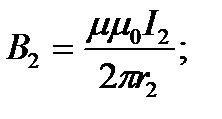
B₁

B a А

B₂

r

D С

I₁ l I₂

Қорытқы өрістің А нүктесіндегі индукциясы шамасын косинустар теоремасы бойынша табамыз: . Есеп шарты бойынша I₁=I₂, r₁=r₂ екендігін ескерсек, жоғарыдағы өрнектерден B₁=B₂ екендігі көрініп тұр. Олай болса,

Осы өрнектегі cosa мәнін табу үшін АДС ұшбұрышынан косинустар теоремасына сүйене отырып мынаны алуға болады 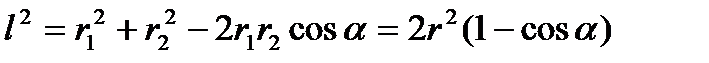. Бұдан

B₁ және cosa үшін жазылған өрнектерді пайдалансақ,

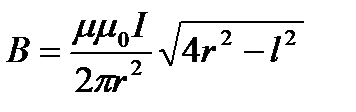
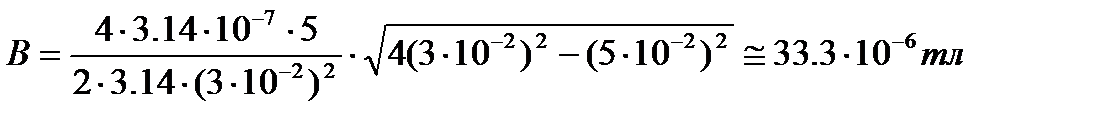
Есеп 3.

Ток күштері I₁ = I₂ = 5,0 А болатын өте ұзын жіңішке екі параллель өткізгіш бір –бірінен вакуумда r = 40 см ара қашықтықта орналасқан. Әр өткізгіштің ұзындық бірлігіне әсер ететін күшті анықтау керек.

Шешуі:

I₁ және I₂ ток күштерінің бағыттары бірдей деп есептейміз (сурет 1).

Бұранда ережесін пайдаланып, B₁ және B₂ индукция векторларының бағытын, өткізгіштен сәйкесінше r қашықтықта орналасқан I₁ және I₂ ток күштерінің магнит өрістерін анықтаймыз.

Ток күші I₂ болатын өткізгіш, I₁ ток күші әсерінен пайда болатын өрісте орналасқан. Осы өрістің магнит индукциясының векторының модулі

.

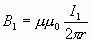Сонымен, ток күші I₂ өткізгіштің кез келген l ұзындығына Ампер заңы бойынша F₁ күші әсер етеді, оның модулі

,

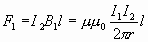мұндағы m ₀ = 4p × 10 ^-7 Гн/м – магниттік тұрақты.

Ток күші I₁ өткізгіштің дәл осындай қимасына F₂ күш әсер етеді, оның модулі F₂ = F₁, ал бағыты F₁ күшіне қарама – қарсы. Сонымен,

Жауабы: F=1,3.10 ^-5 Н.

Date: 2016-05-25; view: 2913; Нарушение авторских прав