
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Проблема размерности в динамическом программировании
|
|
Лекция № 12.
В рассмотренных примерах (задача о загрузке рюкзака и задача о надежности) для описания состояний системы использовалась только одна переменная, одной переменной задавалось и управление. В общем случае в моделях динамического программирования состояния и управления могут быть описаны с помощью нескольких переменных, образующих вектора состояния и управления.
Увеличение количества переменных состояния вызывает рост числа возможных вариантов решения, ассоциированных с каждым из этапов. Это может привести к так называемой проблеме «проклятие размерности», которая является серьезным препятствием при решении задач динамического программирования средней и большой размерности.
В качестве примера рассмотрим задачу о загрузке рюкзака, но уже при двух ограничениях (например, ограничение по весу и по объему):
 (1)
(1)
где  ,
,  . Поскольку в задаче имеется два вида ресурсов
. Поскольку в задаче имеется два вида ресурсов  , то необходимо ввести два параметра состояния
, то необходимо ввести два параметра состояния 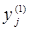 и
и  . Обозначим
. Обозначим  ,
,  ,
,  . Тогда ограничения (1) можно привести к виду:
. Тогда ограничения (1) можно привести к виду:
 (2)
(2)
где  . В рекуррентных уравнениях метода динамического программирования для задачи о «ранце» с двумя ограничениями (1):
. В рекуррентных уравнениях метода динамического программирования для задачи о «ранце» с двумя ограничениями (1):


каждая из функций  ,
,  является функцией двух переменных. Если каждая из переменных
является функцией двух переменных. Если каждая из переменных  ,
,  может принимать 102 значений, то функцию
может принимать 102 значений, то функцию  приходится табулировать в 104 точках. В случае трех параметров
приходится табулировать в 104 точках. В случае трех параметров  при тех же предположениях требуется вычислять 108 степени значений функций
при тех же предположениях требуется вычислять 108 степени значений функций  .
.
Итак, наиболее серьезным препятствием практического применения динамического программирования оказывается число параметров задачи.
Задача управления запасами.
Задача управления запасами возникает, когда необходимо создать запас материальных ресурсов или предметов потребления с целью удовлетворения спроса на заданном интервале времени (конечном или бесконечном). В любой задаче управления запасами требуется определять количество заказываемой продукции и сроки размещения заказов. Спрос можно удовлетворить путём однократного создания запаса на весь рассматриваемый период времени или посредством создания запаса для каждой единицы времени этого периода. Первый случай соответствует избыточному запасу по отношению к единице времени, второй – недостаточному запасу по отношению к полному периоду времени.
При избыточном запасе требуется более высокие удельные (отнесённые к единице времени) капиталовложения, но дефицит возникает реже и частота размещения заказов меньше. С другой стороны, при недостаточном запасе удельные капитальные вложения снижаются, но частота заказов и риск дефицита возрастают. Для любого из указанных крайних случаев характерны значительные экономические потери. Таким образом, решения относительно размера заказа и момента его размещения могут основываться на минимизации соответствующей функции общих затрат, включающих затраты, обусловленные потерями от избыточного запаса и дефицита.
Эти затраты включают в себя:
1. Затраты на приобретение, которые становятся особо важным фактором, когда цена единицы выражается в виде оптовых скидок в тех случаях, когда цена единицы продукции убывает с возрастанием размера заказа.
2. Затраты на оформление заказа представляют собой постоянные расходы, связанные с его размещением. При удовлетворении спроса в течении заданного периода времени путём размещения более мелких заказов (более часто) затраты возрастают по сравнению со случаем, когда спрос удовлетворяется посредством размещения более крупных заказов (и следовательно, реже).
3. Затраты на хранение запаса, которые представляют собой расходы на содержание запаса на складе (процент на инвестированный капитал, амортизационные расходы и эксплуатационные расходы), обычно возрастают с увеличением уровня запасов.
4. Потери от дефицита, обусловленные отсутствием запаса необходимой продукции. Обычно они связаны с экономическими санкциями со стороны потребителей, потенциальными потерями прибыли. На рис.1 иллюстрируется зависимость рассмотренных видов затрат от уровня запаса продукции. На практике какую-либо компоненту затрат можно не учитывать, если она не составляет существенную часть общих затрат. Это приводит к упрощению моделей управления запасами.

Типы моделей управления запасами.
Большое разнообразие моделей управления запасами определяется характером спроса на продукцию, который может быть детерминированным или вероятностным. На рис.2 приведена схема классификации спроса, принимаемая в моделях управления запасами. 
Рис.2
Детерминированный статический спрос предполагает, что интенсивность потребления остаётся неизменной во времени. Динамический спрос - спрос известен, но изменяется в зависимости от времени.
Наиболее точно характер спроса может быть описан посредством вероятностных нестационарных распределений. Однако с математической точки зрения модель значительно усложняется, особенно при увеличении рассматриваемого периода времени.
По существу классификацию на рис.2 можно считать представлением различных уровней абстракции описания спроса.
На первом уровне предполагается, что распределение вероятностей спроса стационарно во времени, т.е. в течение всех исследуемых периодов времени используется одна и та же функция распределения вероятностей. При таком предположении влияние сезонных колебаний спроса в модели не учитывается.
На втором уровне абстракции учитываются изменения спроса от одного периода к другому. Однако при этом функции распределения не применяются, а потребности в каждом периоде описываются средней величиной спроса. Это упрощение означает, что элемент риска в управлении запасами не учитывается. Но оно позволяет исследовать сезонные колебания спроса, которые вследствие аналитических и вычислительных трудностей нельзя учесть в вероятностной модели.
На третьем уровне упрощения предполагается, что спрос в течении любого периода равняется среднему значению известного спроса по всем рассматриваемым периодам, т.е. оценить его постоянной интенсивностью.
Характер спроса является одним из основных факторов при построении модели управления запасами, но имеются и другие факторы, влияющие на выбор типа модели.
1. Запаздывание поставок. После размещения заказа он может быть поставлен немедленно или потребуется некоторое время на его выполнение. Интервал времени между моментом размещения заказа и его поставкой называется запаздыванием поставки. Эта величина может быть детерминированной или случайной.
2. Пополнение запаса. Процесс пополнения запасов может осуществляться мгновенно или равномерно во времени.
3. Период времени определяет интервал, в течение которого осуществляется регулирование уровня запаса. В зависимости от отрезка времени, на котором можно надёжно прогнозировать запас, рассматриваемый период принимается конечным или бесконечным.
4. Число пунктов накопления запасов. В систему управления запасами может входить несколько пунктов хранения запаса. В некоторых случаях эти пункты организованы таким образом, что один выступает в качестве поставщика для другого. Эта схема иногда реализуется на различных уровнях так, что пункт – потребитель одного уровня может стать пунктом – поставщиком на другом. В этом случае имеется система управления с разветвлённой структурой.
5. Число видов продукции. В системе управления запасами может фигурировать более одного вида продукции. Этот фактор учитывается при условии наличия некоторой зависимости между видами продукции. Так, для различных изделий может использоваться одно и тоже складское помещение или же их производство может осуществляться при ограничениях на общие производственные фонды.
Детерминированные модели управления запасами.
1.Детерминированная обобщённая модель определения оптимального размера партии продукции при допущении дефицита.
Рассматривается система управления запасами, когда продукция поступает на склад непосредственно с производственной линии с постоянной интенсивностью  единиц продукции в единицу времени. При достижении некоторого уровня объёма запаса Q производство продукции прекращается. Возобновление производства и поставки продукции на склад осуществляется в момент, когда неудовлетворённый спрос достигнет некоторого значения G. Расходование запаса осуществляется с интенсивностью
единиц продукции в единицу времени. При достижении некоторого уровня объёма запаса Q производство продукции прекращается. Возобновление производства и поставки продукции на склад осуществляется в момент, когда неудовлетворённый спрос достигнет некоторого значения G. Расходование запаса осуществляется с интенсивностью 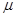 . Известны значения следующих параметров:
. Известны значения следующих параметров:  - стоимость хранения единицы товара на складе в единицу времени;
- стоимость хранения единицы товара на складе в единицу времени;  -стоимость организации заказа (одной партии продукции);
-стоимость организации заказа (одной партии продукции);  - убытки от неудовлетворенного спроса (штраф). Требуется найти оптимальный объём партии продукции и интервал времени между точками возобновления поставки по критерию минимума общих затрат от функционирования системы управления запасами.
- убытки от неудовлетворенного спроса (штраф). Требуется найти оптимальный объём партии продукции и интервал времени между точками возобновления поставки по критерию минимума общих затрат от функционирования системы управления запасами.
Графически условия задачи показаны на рис.3.

Из рисунка видно, что пополнение и расходование запаса осуществляются одновременно в течение интервала  каждого цикла. Накопленный запас Q полностью расходуется в течение интервала
каждого цикла. Накопленный запас Q полностью расходуется в течение интервала  . В течение интервала
. В течение интервала  спрос не удовлетворяется, а накапливается. Неудовлетворённый спрос G покрывается в интервале
спрос не удовлетворяется, а накапливается. Неудовлетворённый спрос G покрывается в интервале  . Величина
. Величина  называется полным циклом управления запасом.
называется полным циклом управления запасом.  - предельный запас продукции, G – предельный дефицит продукции.
- предельный запас продукции, G – предельный дефицит продукции.
Очевидно текущий уровень запаса продукции определяется по формуле:

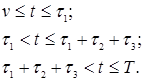
Из треугольника OAB следует:
 или
или  . (1)
. (1)
Аналогично можно определить  ,
,  и
и 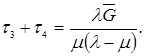 (2)
(2)
Из подобия треугольников OAC и CEF можно записать 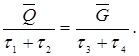 Из равенства следует, что
Из равенства следует, что  (3)
(3)
Выражение (3) с учётом (1) перепишется:
 (4)
(4)
Тогда общая сумма затрат на пополнение, хранение запаса продукции и возможный штраф за неудовлетворительный спрос будет определяться выражением:

 Если привести затраты в единицу времени, то выражение для удельных затрат будет иметь вид:
Если привести затраты в единицу времени, то выражение для удельных затрат будет иметь вид:

Таким образом,  есть функция двух аргументов Q и T, оптимальные значения которых определяются как решение задачи:
есть функция двух аргументов Q и T, оптимальные значения которых определяются как решение задачи:

Для того, чтобы найти минимум функции двух аргументов, необходимо и достаточно решить систему уравнений:
 (5)
(5)
Это следует из факта, что функция  является вогнутой функцией относительно своих аргументов. Решение системы уравнений (5) даёт следующие неотрицательные корни:
является вогнутой функцией относительно своих аргументов. Решение системы уравнений (5) даёт следующие неотрицательные корни:
 (6)
(6)
 (7)
(7)
Минимум общих затрат в единицу времени составит:
 (8)
(8)
Можно рассмотреть частные случаи.
1. Дефицит продукции не допускается. Решение задачи в этом случае получается из формулы (6)-(8), если положить штраф  Тогда С1/С3=0 и оптимальные значения искомых величин будут:
Тогда С1/С3=0 и оптимальные значения искомых величин будут:



Этому случаю соответствует график изменения уровня запаса во времени:

2. Пополнение запаса осуществляется мгновенно. В этом случае полагается  и соответственно
и соответственно 
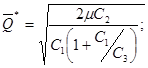


График изменения уровня запаса имеет вид:
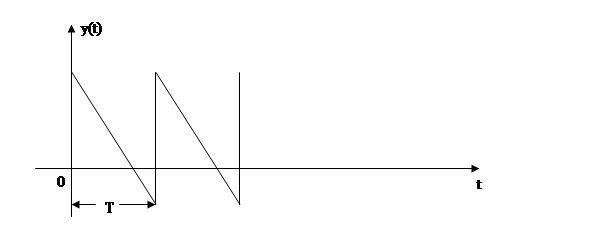
3. Дефицит не допускается, запасы пополняются мгновенно, т.е.  . Тогда следует:
. Тогда следует:



Эти формулы называются формулами Уилсона, а величина  - экономическим размером партии.
- экономическим размером партии.
График изменение уровня запаса имеет вид:

| <== предыдущая | | | следующая ==> |
| Задачу о надежности | | | Элементы теории игр |
Date: 2016-05-25; view: 366; Нарушение авторских прав