
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задачу о надежности
|
|
Пусть конструируется электронный прибор, состоящий из трех основных компонентов. Все компоненты соединены последовательно, поэтому выход из строя одной из них приводит к отказу всего прибора. Надежность (вероятность безотказной работы) прибора можно повысить путем дублирования каждого компонента. Конструкция прибора позволяет использовать  запасных блоков для каждого j-того компонента, т.е. каждый компонент может содержать до
запасных блоков для каждого j-того компонента, т.е. каждый компонент может содержать до  блоков, соединенных параллельно. Общая стоимость прибора не должна превышать С долларов. Если j-тый компонент имеет
блоков, соединенных параллельно. Общая стоимость прибора не должна превышать С долларов. Если j-тый компонент имеет  штук соединенных параллельно блоков, то его надежность составляет
штук соединенных параллельно блоков, то его надежность составляет  и стоимость
и стоимость 
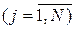 . Требуется определить количество блоков
. Требуется определить количество блоков  в каждом j-том компоненте
в каждом j-том компоненте 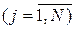 , при котором надежность прибора максимальна, а стоимость прибора не превышает заданной величины С.
, при котором надежность прибора максимальна, а стоимость прибора не превышает заданной величины С.
Построение ММ. По определению, надежность F прибора, состоящего из N последовательно соединенных компонентов, каждый из которых включает  параллельно соединенных блоков, равна произведению надежности компонент. Тогда ММ имеет вид:
параллельно соединенных блоков, равна произведению надежности компонент. Тогда ММ имеет вид:
 (7)
(7)
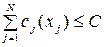 (8)
(8)
 ,
, 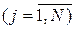 (9)
(9)
Из физического смысла задачи следует, что  ,
,  >0 для всех допустимых
>0 для всех допустимых  .
.
Введем дополнительную переменную  - количество средств, израсходованных на дублирование компонент 1,2,… j-1. Тогда можно записать:
- количество средств, израсходованных на дублирование компонент 1,2,… j-1. Тогда можно записать:
 (10)
(10)
 (11)
(11)
Из (10) следует:  . Тогда с учетом (9) область допустимых значений
. Тогда с учетом (9) область допустимых значений  будет иметь вид
будет иметь вид  , а рекуррентные соотношения Беллмана принимают вид:
, а рекуррентные соотношения Беллмана принимают вид:
 (12).
(12).
 (13)
(13)
Покажем применение рекуррентных соотношений Беллмана для решения задачи (7)-(9), решаемых в порядке  . Проводя преобразования, аналогичные преобразованиям задачи о загрузке рюкзака, получим:
. Проводя преобразования, аналогичные преобразованиям задачи о загрузке рюкзака, получим:
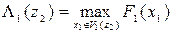


Здесь  ,
,  есть область изменения
есть область изменения  при фиксированном
при фиксированном  .
.
Date: 2016-05-25; view: 710; Нарушение авторских прав