Метод динамического программирования

Лекция № 10.

ДП представляет собой математический аппарат, разработанный с целью повышения эффективности вычислений при решении некоторого класса задач мат. программирования путем их декомпозиции на относительно небольшие и, следовательно, менее сложные задачи. Характерным для ДП является подход к решению задачи по этапам, с каждым из которых ассоциирована одна управляемая переменная. Набор рекуррентных вычислительных процедур, связывающий различные этапы, обеспечивает получение решения задачи при достижении последнего этапа.

Рассмотрим функционирование некоторого объекта в течение промежутка времени Т. Пусть в момент времени t_j состояние объекта характеризуется вектором , причем в начальный момент времени t₁ состояние объекта задано, т.е. вектор известен. Объект меняет свое состояние под воздействием управления в моменты времени . При этом управляющее воздействие выбирается из заданной области , т.е.

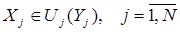(1)

Рассматривается случай, когда будущее состояние объекта зависит только от состояния объекта в данный момент времени и управляющего воздействия в этот момент времени, т.е.

. (2)

Здесь - заданная функция своих аргументов. Уравнение (2) является уравнением движения объекта, т.е. описывает динамику объекта во времени.

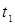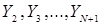Обозначим -выигрыш, получаемый от функционирования объекта на j -м участке времени, т.е. в полуинтервале . Если в момент времени , когда объект находился в состоянии выбрать управление , то объект перейдет в состояние . Далее последовательно можно выбирать в соответствии с (1) , в из (2) определять . Этим значениям и 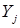будет соответствовать вполне определенное значение дохода:

(3)

Если выбирать другие значения управляющих воздействий, то им будут соответствовать другие состояния объекта, а следовательно, и другое значение общего дохода (3). Поэтому естественно поставить следующую оптимизационную задачу:

(4)

. (5)

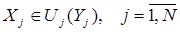(6)

- задан. (7)

Здесь необходимо найти неизвестные и 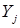, которые удовлетворяли бы ограничениям (5)-(7) и максимизировали бы целевую функцию (4).

Эта задача является в общем случае задачей нелинейного программирования и обладает следующими особенностями:

1. Искомые переменные разбиты на N групп, в каждую j-тую из которых входят только и .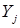

2. Целевая функция (4) является суммой функций , каждая из которых зависит лишь от переменных соответствующей группы. В этом случае говорят, что целевая функция сепарабельна, или аддитивна.

3. Уравнение (5) является рекуррентным, т.е. через значения и 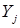однозначно определяется .

Многие реальные задачи ИСО сводятся к ММ вида (4)-(7), которая допускает различные интерпретации.

Решение задачи вида (4)-(7) обычными методами оказывается либо невозможным, либо неэффективным из-за большой размерности. Поэтому ее решение сводится к последовательному решению N связанных между собой задач меньшей размерности. Для выявления этих задач и связей между ними рассмотрим задачу вида (4)-(7), соответствующую последним этапам . Она запишется в виде:

(8)

. (9)

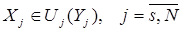(10)

- фиксирован. (11)

В этой задаче мы не знаем, чему равно конкретное значение , но если его зафиксировать, то получим соответствующее максимальное значение (8). Если зафиксировать другое значение , то естественно максимальное значение целевой функции (8) будет другим. Обозначим максимальное значение целевой функции (8)при некотором зафиксированном через :

Запишем это равенство в виде:

(12)

Здесь первое слагаемое не зависит от , а вторая сумма функций зависит от . Поэтому выражение (12) можно переписать в виде:

Таким образом окончательно запишем:

(13)

Данное соотношение справедливо для всех , а для 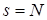имеем:

(14)

Полученные рекуррентные соотношения являются основными соотношениями МДП. Это так называемые соотношения Беллмана. Они позволяют свести решение ЗНП (4)-(7) к последовательному решению N задач максимизации меньшей размерности.

Соотношение (13) позволяет вычислить , если известно , а (14) позволяет вычислить максимальное значение целевой функции на последнем этапе. Тогда рекуррентный процесс решения задачи (13)-(14) должен проводиться в порядке 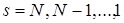. Действительно, зная 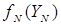из (13) можно найти значения 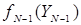и т.д.

Рассмотрим алгоритм решения такой задачи.

1 шаг. Решается задача (14):

.

Решается столько однотипных задач, сколько существует возможных значений фиксированных . Здесь максимизируется функция по переменной для каждого возможного фиксированного значения . Решается столько однотипных задач, сколько существует возможных значений фиксированных . Поэтому для каждого в результате получаются условные точки максимума 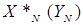и максимальное значение функции в этих точках.

2 шаг. На этом шаге решается задача (13) при :

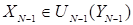Здесь решаются задачи максимизации функции по переменной при каждом возможном фиксированном значении . В результате находятся условные точки максимума и значения суммы двух функций в этих точках .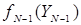

Далее, зная 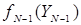, решается задача (13) для 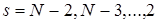. Наконец, при 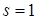переходим к шагу N:

N шаг. 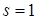, . На этом шаге решается только одна задача оптимизации, т.к. - задан. В результате получим точку максимума и значение .

Для окончательного решение проводим обратное движение алгоритма:

1 шаг: ; .

2 шаг: ; .

3 шаг: ; .

…

N шаг: ; .

.

Таким образом, определяется решение исходной ЗНП (4)-(7) как 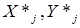, при этом максимальное значение целевой функции (4) будет равно значению .

Date: 2016-05-25; view: 378; Нарушение авторских прав