
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определения из учебников
|
|
А. В. Погорелов. Геометрия: Учебник для 10 – 11 классов общеобразовательных учреждений [Погорелов10-11]
Для изображения пространственных фигур на плоскости обычно пользуются параллельным проектированием. Этот способ изображения состоит в следующем. Берем произвольную прямую 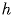 , пересекающую плоскость чертежа
, пересекающую плоскость чертежа  , проводим через произвольную точку
, проводим через произвольную точку  фигуры прямую, параллельную
фигуры прямую, параллельную 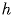 . Точка
. Точка  пересечения этой прямой с плоскостью чертежа будет изображением точки
пересечения этой прямой с плоскостью чертежа будет изображением точки  . Построив таким образом изображение каждой точки фигуры, получим изображение самой фигуры.
. Построив таким образом изображение каждой точки фигуры, получим изображение самой фигуры.
В черчении применяется ортогональное проектирование, т.е. параллельное проектирование прямыми, перпендикулярными плоскости проекции.
В.М.Клопский, З.А.Скопец, М.И.Ягодовский. Геометрия. Учебное пособие для 9 и 10 классов средней школы [КлопскийСкопецЯгодовский9-10]
Пусть дана плоскость  и прямая
и прямая  , пересекающая
, пересекающая  . Возьмем произвольную точку
. Возьмем произвольную точку  ; через нее проведем прямую
; через нее проведем прямую  , параллельную прямой
, параллельную прямой  . Прямая
. Прямая
 пересечет
пересечет  в некоторой точке
в некоторой точке  . Полученную таким образом точку
. Полученную таким образом точку  назовем проекцией точки
назовем проекцией точки  на плоскость
на плоскость  при проектировании параллельно прямой
при проектировании параллельно прямой  (короче, точка
(короче, точка  --- параллельная проекция точки
--- параллельная проекция точки  ). Параллельной проекцией фигуры
). Параллельной проекцией фигуры  назовем множество
назовем множество  параллельных проекций всех точек данной фигуры.
параллельных проекций всех точек данной фигуры.
В стереометрии изображением фигуры (оригинала) будем называть любую фигуру, подобную параллельной проекции данной фигуры на некоторую плоскость.
Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Л. С. Киселева, Э. Г. Позняк. Геометрия: Учебник для 10 – 11 классов общеобразовательных учреждений [Атанасян10-11]
Пусть  --- некоторая плоскость, а
--- некоторая плоскость, а  --- пересекающая эту плоскость прямая. Отметим произвольную точку
--- пересекающая эту плоскость прямая. Отметим произвольную точку  пространства. Если точка
пространства. Если точка  не лежит на прямой
не лежит на прямой  , то проведем через
, то проведем через  прямую, параллельную прямой
прямую, параллельную прямой  , и обозначим через
, и обозначим через  точку пересечения этой прямой с плоскостью
точку пересечения этой прямой с плоскостью  . Если же
. Если же  --- точка прямой
--- точка прямой  , то обозначим через
, то обозначим через  точку пересечения прямой
точку пересечения прямой  с плоскостью
с плоскостью  . Точка
. Точка  называется проекцией точки
называется проекцией точки  на плоскость
на плоскость  при проектировании параллельно прямой
при проектировании параллельно прямой  . Обычно предполагается, что плоскость
. Обычно предполагается, что плоскость  и прямая
и прямая  заданы, поэтому точку
заданы, поэтому точку  кратко называют параллельной проекцией точки
кратко называют параллельной проекцией точки  .
.
Пусть  --- плоская или пространственная фигура. Параллельные проекции всех точек фигуры
--- плоская или пространственная фигура. Параллельные проекции всех точек фигуры  образуют некоторую фигуру на плоскости
образуют некоторую фигуру на плоскости  . Фигура
. Фигура  называется параллельной проекцией фигуры
называется параллельной проекцией фигуры  . Говорят также, что фигура
. Говорят также, что фигура  получена из фигуры
получена из фигуры  параллельным проектированием.
параллельным проектированием.
Выберем некоторую плоскость  и назовём ее плоскостью изображений. Затем возьмем прямую
и назовём ее плоскостью изображений. Затем возьмем прямую  , пересекающую плоскость
, пересекающую плоскость  , и спроектируем данную фигуру
, и спроектируем данную фигуру  на плоскость
на плоскость  параллельно прямой
параллельно прямой  . Полученную плоскую фигуру
. Полученную плоскую фигуру  или любую подобную ей фигуру
или любую подобную ей фигуру  на плоскости
на плоскости  будем называть изображением фигуры
будем называть изображением фигуры  .
.
А.Д. Александров, А.Л. Вернер, В.И. Рыжик. Геометрия: учебник для 10-11 классов общеобразовательных учреждений [АлександровВернерРыжик10-11]
Пусть даны плоскость  и пересекающая ее прямая
и пересекающая ее прямая  . Возмем в пространстве произвольную точку
. Возмем в пространстве произвольную точку 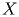 . В том случае, когда точка
. В том случае, когда точка 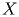 не лежит на
не лежит на  , через
, через 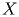 проведем прямую
проведем прямую  . Прямая
. Прямая  пересекает плоскость
пересекает плоскость  в некоторой точке
в некоторой точке  . Эта точка называется проекцией (на плоскость
. Эта точка называется проекцией (на плоскость  ) точки
) точки 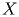 при проектировании параллельно прямой
при проектировании параллельно прямой  . Если же точка
. Если же точка 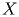 лежит на прямой
лежит на прямой  , то ее параллельной проекцией
, то ее параллельной проекцией  называется точка, в которой
называется точка, в которой  пересекает
пересекает  . О прямой
. О прямой  говорят, что она задает направление проектирования.
говорят, что она задает направление проектирования.
А.Д. Александров, А.Л. Вернер, В.И. Рыжик. Учебник для 10 класса школ с углубленным изучением математики [АлександровВернерРыжик10у]
Пусть даны плоскость  и пересекающая ее прямая
и пересекающая ее прямая  . Возмем в пространстве произвольную точку
. Возмем в пространстве произвольную точку 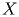 . В том случае, когда точка
. В том случае, когда точка 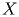 не лежит на
не лежит на  , через
, через 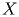 проводим прямую
проводим прямую  , параллельную прямой
, параллельную прямой  . Прямая
. Прямая  пересекает плоскость
пересекает плоскость  в некоторой точке
в некоторой точке  . Эта точка называется проекцией (на плоскость
. Эта точка называется проекцией (на плоскость  ) точки
) точки 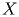 при проектировании параллельно прямой
при проектировании параллельно прямой  или, короче, параллельной проекцией точки
или, короче, параллельной проекцией точки 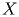 .
.
Если точка 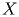 лежит на прямой
лежит на прямой  , то ее параллельной проекцией
, то ее параллельной проекцией  называется точка, в которой
называется точка, в которой  пересекает
пересекает  .
.
Плоскость  назывется плоскостью проекций.
назывется плоскостью проекций.
О прямой  говорят, что она задает направление проектирования.
говорят, что она задает направление проектирования.
Проекцией фигуры  называется множество
называется множество  проекций всех ее точек. Отображение, сопоставляющее каждой точке
проекций всех ее точек. Отображение, сопоставляющее каждой точке 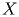 фигуры
фигуры  ее параллельную проекцию
ее параллельную проекцию  , называется параллельным проектированием фигуры
, называется параллельным проектированием фигуры  .
.
И. М. Смирнова. Геометрия. 10-11 классы: Учебник для общеобразовательных учреждений (гуманитарный профиль) [Смирнова10-11гум]
Пусть  --- произвольная плоскость,
--- произвольная плоскость,  --- пересекающая ее прямая. Через некоторую точку
--- пересекающая ее прямая. Через некоторую точку  , не принадлежащую прямой
, не принадлежащую прямой  , проведем прямую, параллельную прямой
, проведем прямую, параллельную прямой  . Точка пересечения этой прямой с плоскостью
. Точка пересечения этой прямой с плоскостью  называется параллельной проекцией точки
называется параллельной проекцией точки  на плоскость
на плоскость  в направлении прямой
в направлении прямой  . Обозначим ее
. Обозначим ее  . Если точка
. Если точка  принадлежит прямой
принадлежит прямой  , то параллельной проекцией
, то параллельной проекцией  на плоскость
на плоскость  считается точка пересечения прямой
считается точка пересечения прямой  с плоскостью
с плоскостью  .
.
Таким образом, каждой точке  пространства сопоставляется ее проекция
пространства сопоставляется ее проекция  на плоскость
на плоскость  . Это соответствие называется параллельным проектированием на плоскость
. Это соответствие называется параллельным проектированием на плоскость  в направлении прямой
в направлении прямой  .
.
Пусть  --- некоторая фигура в пространстве. Проекции ее точек на плоскость
--- некоторая фигура в пространстве. Проекции ее точек на плоскость  образуют фигуру
образуют фигуру  , которая называется параллельной проекцией фигуры
, которая называется параллельной проекцией фигуры  на плоскость
на плоскость  в направлении прямой
в направлении прямой  . Говорят также, что фигура
. Говорят также, что фигура  получена из фигуры
получена из фигуры  параллельным проектированием.
параллельным проектированием.
Для изображения пространственных фигур используют параллельную проекцию. Плоскость, на которую проектируется фигура, называется плоскостью изображений, а сама проекция фигуры --- изображением.
И. М. Смирнова, В. А. Смирнов. Геометрия. 10 – 11 класс: Учебник для общеобразовательных учреждений [СмирноваСмирнов10-11]
Пусть  --- некоторая плоскость,
--- некоторая плоскость,  --- пересекающая ее прямая. Через некоторую точку
--- пересекающая ее прямая. Через некоторую точку  , не принадлежвщую прямой
, не принадлежвщую прямой  , проведем прямую, параллельную прямой
, проведем прямую, параллельную прямой  . Точка пересечения этой прямой с плоскостью
. Точка пересечения этой прямой с плоскостью  называется параллельной проекцией точки
называется параллельной проекцией точки  на плоскость
на плоскость  в направлении прямой
в направлении прямой  . Обозначим ее
. Обозначим ее  . Если точка
. Если точка  принадлежит прямой
принадлежит прямой  , то параллельной проекцией
, то параллельной проекцией  на плоскость
на плоскость  считается точка пересечения прямой
считается точка пересечения прямой  с плоскостью
с плоскостью  .
.
Таким образом, каждой точке  пространства сопоставляется ее проекция
пространства сопоставляется ее проекция  на плоскость
на плоскость  . Это соответствие называется параллельным проектированием на плоскость
. Это соответствие называется параллельным проектированием на плоскость  в направлении прямой
в направлении прямой  .
.
Пусть  --- некоторая фигура в пространстве. Проекции ее точек на плоскость
--- некоторая фигура в пространстве. Проекции ее точек на плоскость  образуют фигуру
образуют фигуру  , которая называется параллельной проекцией фигуры
, которая называется параллельной проекцией фигуры  на плоскость
на плоскость  в направлении прямой
в направлении прямой  . Говорят также, что фигура
. Говорят также, что фигура  получена из фигуры
получена из фигуры  параллельным проектированием.
параллельным проектированием.
Для изображения пространственных фигур используют параллельную проекцию. Плоскость, на которую проектируется фигура, называется плоскостью изображений, а сама проекция фигуры --- изображением.
Е. В. Потоскуев, Л. И. Звавич. Геометрия 10 класс: учебник для общеобразовательных учреждений с углубленным и профильным изучением математики [ПотоскуевЗвавич10у]
В пространстве выбирается плоскость  , которую называют плоскостью проекций или плоскостью изображения, и прямая
, которую называют плоскостью проекций или плоскостью изображения, и прямая  , пересекающая эту плоскость. Пусть
, пересекающая эту плоскость. Пусть  --- произвольная точка пространства. Через эту точку проведем прямую
--- произвольная точка пространства. Через эту точку проведем прямую  , параллельную
, параллельную  . Точка
. Точка  пересечения прямой
пересечения прямой  с плоскостью
с плоскостью  называется параллельной проекцией точки
называется параллельной проекцией точки  на плоскость
на плоскость  в направлении прямой
в направлении прямой  . Если
. Если  --- точка плоскости
--- точка плоскости  , то
, то  совпадает с
совпадает с  .
.
При этом часто пользуются обозначением  .
.
Прямую  и все прямые пространства, параллельные ей, называют проектирующими прямыми; они определяют направление проектирования. Всякая плоскость пространства, параллельная проектирующей прямой, называется проектирующей плоскостью.
и все прямые пространства, параллельные ей, называют проектирующими прямыми; они определяют направление проектирования. Всякая плоскость пространства, параллельная проектирующей прямой, называется проектирующей плоскостью.
Фигура, которую проектируют или изображают, называется оригиналом.
И. Ф. Шарыгин. Геометрия 10-11 классы: Учебник для общеобразовательных учебных заведений [Шарыгин10-11]
Пусть в пространстве заданы прямая  и плоскость
и плоскость  , не параллельные друг другу.
, не параллельные друг другу.
(Параллельной) проекцией точки  на плоскость
на плоскость  в направлении
в направлении  мы будем называть точку пересечения с
мы будем называть точку пересечения с  прямой, проходящей через
прямой, проходящей через  и параллельной
и параллельной  .
.
(Ортогональной) проекцией точки  на плоскость
на плоскость  называется точка пересечения с плоскостью
называется точка пересечения с плоскостью  прямой, проходящей через
прямой, проходящей через  и перпендикулярной
и перпендикулярной  .
.
(Параллельной) проекцией фигуры  на плоскость
на плоскость  назывется фигура
назывется фигура  этой плоскости, образованная (параллельными) проекциями всех точек фигуры
этой плоскости, образованная (параллельными) проекциями всех точек фигуры  .
.
А. П. Киселев, Н. А. Рыбкин. Геометрия: Стереометрия: 10 – 11 классы: Учебник и задачник [Киселев10-11]
1) Ортогональной (или прямоугольной) проекцией какой-нибудь точки на данную плоскость называется основание перпендикуляра, опущенного на эту плоскость из взятой точки.
2) Ортогональной проекцией какой-нибудь линии на плоскость называется геометрическое место проекций всех точек этой плоскости.
Для краткости речи вместо "ортогональная проекция" будем говорить просто "проекция".
ЗАДАЧИ!!!!!!!!!!!!!
Условие
Найдите сторону правильного треугольника, являющегося ортогональной проекцией треугольника со сторонами  , 3 и
, 3 и  на некоторую плоскость.
на некоторую плоскость.
Решение
Пусть треугольник ABC, в котором AB =  , BC =
, BC =  и AC = 3, ортогонально проектируется на плоскость a и его проекцией является равносторонний треугольник. Будем считать, что вершина A лежит в плоскости a. Докажем, что тогда вершины B и C должны располагаться по одну сторону от плоскости a. Предположим, что это не так. Пусть точки B и C расположены по разные стороны от плоскости a (рис.1), а B 1и C 1– ортогональные проекции этих точек на плоскость a. Тогда в треугольнике BC 1 C угол при вершине C 1– тупой, поэтому BC > BC 1. В то же время, BC 1 = AB как гипотенузы равных прямоугольных треугольников AB 1 B и C 1 B 1 B. Значит, BC > AB, что невозможно, т.к. AB – наибольшая сторона треугольника ABC. Обозначим AB 1 = AC 1 = B 1 C 1 = x, BB 1 = z, CC 1 = y (рис.2). Из прямоугольных треугольников AB 1 B, AC 1 C и из прямоугольной трапеции BB 1 C 1 C находим, что
и AC = 3, ортогонально проектируется на плоскость a и его проекцией является равносторонний треугольник. Будем считать, что вершина A лежит в плоскости a. Докажем, что тогда вершины B и C должны располагаться по одну сторону от плоскости a. Предположим, что это не так. Пусть точки B и C расположены по разные стороны от плоскости a (рис.1), а B 1и C 1– ортогональные проекции этих точек на плоскость a. Тогда в треугольнике BC 1 C угол при вершине C 1– тупой, поэтому BC > BC 1. В то же время, BC 1 = AB как гипотенузы равных прямоугольных треугольников AB 1 B и C 1 B 1 B. Значит, BC > AB, что невозможно, т.к. AB – наибольшая сторона треугольника ABC. Обозначим AB 1 = AC 1 = B 1 C 1 = x, BB 1 = z, CC 1 = y (рис.2). Из прямоугольных треугольников AB 1 B, AC 1 C и из прямоугольной трапеции BB 1 C 1 C находим, что
x 2 + y 2 = 14, x 2 + z 2 = 9, x 2 + (y - z)2 = 6.
Вычитая почленно первое уравнение из второго и третьего, получим систему

Далее имеем:
y =  , z 2 -
, z 2 -  + 5 = 0, 4 z 4 - z 4 - 16 z 2 - 64 + 20 z 2 = 0,
+ 5 = 0, 4 z 4 - z 4 - 16 z 2 - 64 + 20 z 2 = 0,
3 z 4 + 4 z 2 - 64 = 0, z 2 = 4, x 2 = 9 - z 2 = 5.
Следовательно, x =  .
.
Ответ
 .
.
Условие
Дано изображение (параллельная проекция на некоторую плоскость) треугольника и центра описанной около него окружности. Постройте изображение точки пересечения высот этого треугольника.
Решение
При параллельном проектировании сохраняется отношение отрезков, лежащих на одной прямой или на параллельных прямых. Поэтому изображениями середин M и N сторон AB и AC треугольника ABC являются середины M 1и N 1сторон A 1 B 1и A 1 C 1треугольника A 1 B 1 C 1– изображения треугольника ABC. Пусть H – точка пересечения высот треугольника ABC. Тогда CH || OM и BH || ON, где O – центр описанной окружности треугольника ABC. При параллельном проектирование сохраняется параллельность прямых. Поэтому C 1 H 1 || O 1 M 1и B 1 H 1 || O 1 N 1, где O 1– изображение точки O. Отсюда выстекает следующее построение. Строим середины M 1и N 1данных сторон A 1 B 1и A 1 C 1. Через точки C 1и B 1проводим прямые, параллельные O 1 M 1и O 1 N 1соответственно. Точка H 1пересечения построенных прямых есть искомое изображение точки пересечения высот треугольника ABC.
Условие
На плоскости нарисована линия, являющаяся изображением (параллельной проекцией на некоторую плоскость) окружности. Постройте изображение центра этой окружности.
Решение
Пусть A 1 B 1– изображение хорды AB окружности, M – середина AB. Поскольку при параллельном проектировании середина отрезка переходит в середину проекции этого отрезка, то изображение M 1точки M есть середина A 1 B 1. Известно, что прямая, проходящая через середины двух параллельных хорд окружности, проходит через центр окружности. Кроме того, при параллельном проектировании сохраняется параллельность прямых. Отсюда вытекает следующее построение. Строим два параллельных отрезка с концами на данном изображении окружности. Затем проводим прямую через середины этих отрезков. Таким образом, мы построили изображение P 1 Q 1какого-то диаметра PQ окружности. Середина O 1отрезка P 1 Q 1есть изображение центра окружности.
Условие
На плоскости даны изображение (параллельная проекция) плоского четырёхугольника ABCD и точки M, не лежащей в его плоскости. Постройте изображение прямой, по которой пересекаются плоскости ABM и CDM.
Решение
Пусть A 1, B 1, C 1, D 1– изображения вершин соответственно A, B, C, D четырёхугольника ABCD, M 1– изображение точки M. Если прямые AB и CD параллельны (рис.1), то по теореме о пересекающихся плоскостях, проходящих через две параллельные прямые, прямая пересечения плоскостей ABM и CDM параллельна каждой из прямых AB и CD. При параллельном проектировании сохраняется параллельность прямых. Значит, изображение прямой пересечения плоскостей ABM и CDM есть прямая, проходящая через точку M 1параллельно A 1 B 1и C 1 D 1. Если прямые AB и CD пересекаются в точке E, изображение E 1точки E есть точка пересечения прямых A 1 B 1и C 1 D 1(рис.2). В этом случае изображением прямой пересечения плоскостей ABM и CDM является прямая M 1 E 1.
Условие
Плоскость пересекает ребра AB, AC, DC и DB тетраэдра ABCD в точках M, N, P и Q соответственно, причем AM: MB = m, AN: NC = n, DP: PC = p. Найдите отношение BQ / QD.
Решение
Если прямая NP параллельна прямой AD, то NP параллельна плоскости ABD. В этом случае секущая плоскость пересекает плоскость ABD по прямой MQ, параллельной прямой NP, поэтому BQ: QD = BM: MA = 1: m.
Пусть теперь прямая NP пересекает прямую AD в точке T, лежащей на продолжении ребра AD за точку D. Тогда прямая MT пересекает ребро BD в точке Q.
Рассмотрим плоскость треугольника ADC. Через вершину C проведем прямую, параллельную AD. Пусть L - точка пересечения этой прямой с прямой NP. Из подобия треугольников CLP и DTP следует, что
CL = DT . CP / PD = DT / p,
а из подобия треугольников CLN и ATN -
AT = CL . AN / NC = CL . n = DT . n / p.
Рассмотрим теперь плоскость треугольника ABD. Через вершину B проведем прямую, параллельную AD, и продолжим TM до пересечения с этой прямой в точке E. Из подобия треугольников AMT и BME находим, что
BE = AT . BM / AM = AT / m,
а из подобия треугольников TQD и EQB -
BQ / QD = BE / DT = (AT / m)/ DT = (DT . n /(pm))/ DT = n /(mp).
Ответ n/(mp).
Условие
а) Сумма длин рёбер любого выпуклого многогранника больше утроенного диаметра. Докажите это. (Диаметром многогранника называют наибольшую из длин всевозможных отрезков с концами в вершинах многогранника.)
б) Для любых двух вершин A и B любого выпуклого многогранника существуют три ломаные, каждая из которых идёт по рёбрам многогранника из А в В и никакие две не проходят по одному ребру. Докажите это.
в) Если в выпуклом многограннике разрезать два ребра, то для любых двух его вершин А и В существует соединяющая эти две вершины ломаная, идущая по оставшимся рёбрам. Докажите это.
г) Докажите, что в задаче б) можно выбрать три ломаные, никакие две из которых не имеют общих вершин, за исключением точек А и В.
Решение
Очевидно, что из задачи г) следует задача б), из б) следуетв) и а). Заметим еще, что с помощью теоремы Форда-Фалкерсона о максимальном потоке и минимальном разрезе (см. "Квант" #4, 1970г., стр.24, задача 4) легко из в) вывести б); достаточно применить эту теорему к сети, образуемой ребрами многогранника (каждое ребро считается дважды – "туда" и "обратно"). Мы приведем набросок коротких доказательств а) и в) и решим г).
а) Пусть AB – диаметр M. Спроектируем все ребра M на AB.
Посмотрим, сколько точек проектируется в какую-нибудь точку C, лежащую внутри AB. Если через C провести плоскость P перпендикулярно AB, то P пересечет AB по выпуклому многоугольнику. Вершины этого многоугольника (а их не меньше трех!) суть точки пересечения P с ребрами M и, значит, в каждую внутреннюю точку отрезка AB проектируется не менее трех ребер M. Отсюда легко вывести утверждение задачи а).
При решении задач в) и г) мы будем использовать следующее интуитивно очевидное утверждение: для любых двух вершин A и B выпуклого многогранника M существует путь из A в B по ребрам M. Доказательство мы оставляем читателю.
в) Пусть разрезаны ребра r1 и r2. Очевидно, что существует путь L1, соединяющий концы r1 и не проходящий через r2.
Действительно, к ребру r1 прилегают две грани. Ребро r2 не лежит хотя бы на одной из этих граней, поэтому за L1 можно взять путь по ее границе. Аналогично, для ребра r2 существует путь L2.
Рассмотрим теперь две произвольные вершины A и B. Как было сказано выше, существует путь L, идущий из A в B по ребрам M. Заменив в пути L ребро r1 на путь L1, а ребро r2 на путь L2 (если, конечно, эти ребра встречаются в L), мы получим искомый путь по оставшимся ребрам. Заметим, что этот путь может иметь самопересечения, которые, впрочем, нетрудно устранить.
г) Как было сказано выше, для любых двух вершин A, B выпуклого многогранника найдется путь из A в B, идущий по ребрам. Назовем длиной такого пути число ребер, из которых он состоит, и назовем расстоянием между A и B – обозначим его через d (A,B)– длину кратчайшего (по числу ребер) пути.
Для доказательства утверждения задачи мы фиксируем точку A и будем проводить индукцию по расстоянию между точками A и B.
Если d (A,B) = 1, то A и B лежат на одном ребре, и утверждение очевидно, так как можно пройти из A в B по ребру AB и границам двух граней, прилегающих к AB.
Предположим, что утверждение доказано для всех вершин, лежащих от A на расстоянии n - 1. Пусть d (A,B) =n. Тогда существует вершина B' такая, что d (A,B) = n - 1и d (B',B) = 1. Рассмотрим все грани, содержащие B'. Множество всех ребер, принадлежащих всем таким граням, состоит из "радиусов" (ребер с концом B') и "кольца" (которое образуют остальные ребра). Одной из вершин кольца является точка B. По предположению индукции существуют три пути l1, l2, l3 из A в B', не имеющие попарно общих точек, кроме концов. Очевидно, что каждый из этих трех путей проходит хотя бы через одну вершину кольца. Такие вершины кольца назовем занятыми.
Будем теперь двигаться из точки B по кольцу в одном направлении, пока не попадем в первую занятую вершину, а затем в другом направлении. Рассмотрим две полученные занятые вершины A1 и A2 (одна из них может быть вершиной B). Возможны два случая.
Случай 1. Занятые вершины A1 и A2 принадлежат разным путям, скажем l1 и l2. Тогда мы строим три пути из A в B следующим образом.
Первый путь: из A в A1 по l1, затем из A1 в B по кольцу (заметим, что по построению точки A1 на последнем участке мы не пересекаемся с путями l2 и l3).
Второй путь: из A в A2 по l2, затем из A2 в B по кольцу.
Третий путь: из A в B' по l3, затем по ребру B'B.
Очевидно, что построенные три пути попарно не имеют общих точек, кроме концов.
Случай 2. Занятые вершины A1 и A2 принадлежат одному пути, скажем l1. Посмотрим тогда, какая на этих вершин встречается раньше при движении от A к B' по l1 и возьмем отрезок l'1 пути l1 от A до первой из этих вершин. После этого рассмотрим три пути l'1, l2, l3, рассмотрим множество вершин кольца, занятых путями l'1, l2, l3 и проведем снова предыдущие рассуждения применительно к этим трем путям.
Если нам встретится случай 1, то мы построим искомые пути описанным выше способом, если же снова встретится случай 2, то мы рассмотрим новую тройку путей l''1, l2, l3. Если и для этой тройки возникнет случай 2, то мы рассмотрим новую тройку и т.д. Поскольку мы при этом отходим по кольцу все дальше и на кольце есть вершины, принадлежащие путям l2 и l3, то на некотором шаге мы получим случай 1 и искомые пути из A в B будут построены.
Задача г) решена.
Верно еще более сильное утверждение: для любых двух вершин A и B можно найти три цепочки граней, не имеющие общих граней и в каждой из которых первая грань содержит вершину A, последняя – вершину B и соседние грани имеют общее ребро.
Условие
Date: 2016-05-25; view: 1274; Нарушение авторских прав