Нормальное распределение (распределение Гаусса)

Нормальное распределение (распределение Гаусса) используется при оценке надежности изделий, на которые воздействует ряд случайных факторов, каждый из которых незначительно влияет на результирующий эффект (нет доминирующих факторов). Доказывается [3], что сумма достаточно большого числа независимых (или слабо зависимых) СВ, подчиненных каким угодно законам распределения (при соблюдении некоторых нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество СВ суммируется. Основное ограничение, налагаемое на суммируемые СВ, состоит в том, чтобы они все равномерно играли в общей сумме относительно малую роль. Если это условие не выполняется и, например, одна из СВ окажется по своему влиянию на сумму резко превалирующей над всеми другими, то закон распределения этой превалирующей СВ наложит свое влияние на сумму и определит в основных чертах ее закон распределения.

Нормальный закон распределения характеризуется частотой отказов a (t) или плотностью вероятности отказов f (t) вида:

, (5.36)

где σ– среднеквадратическое отклонение СВ x;

m x – математическое ожидание СВ x. Этот параметр часто называют центром рассеивания или наиболее вероятным значением СВ Х.

x – случайная величина, за которую можно принять время, значение тока, значение электрического напряжения и других аргументов.

Нормальный закон – это двухпараметрический закон, для записи которого нужно знать m x и σ.

Вероятность безотказной работы при данном законе распределения определяется по формуле:

. (5.37)

Интенсивность отказов можно определить по следующей формуле:

. (5.38)

Кривая распределения по нормальному закону имеет симметричный холмообразный вид (рисунок 5.9).

Выясним, как влияет на форму и расположение нормальной кривой значения параметров т и σ. Из формулы (5.36) видно, что центром симметрии распределения является центр рассеивания т. Это ясно из того, что при изменении знака разности (х — т) на обратный результат в выражении (5.36) не меняется. Если изменять центр рассеивания т, кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рисунок 5.10).

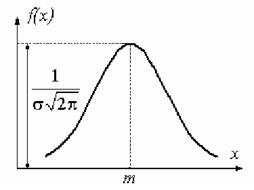
Рисунок 5.9 – Кривая распределения нормального

закона

Рисунок 5.10 — Смещение кривой нормального распределения с изменением т

Размерность центра рассеивания — та же, что и размерность случайной величины Х.

Параметр σ (среднее квадратическое отклонение) характеризует не положение, а саму форму кривой распределения. С увеличением σ кривая растягивается и становится более плоской, с уменьшением σ она вытягивается вверх и сжимается. Это объясняется тем, что площадь под кривой распределения всегда остается равной единице, несмотря на изменение максимума плотности вероятности. На рисунке 5.11 показаны три нормальные кривые при различных σ.

Рисунок 5.11 – Изменение формы кривой распределения с изменением σ

Размерность параметра σсовпадает с размерностью СВ Х. Во многих задачах практики приходится определять вероятность попадания СВ Х, подчиненной нормальному закону с произвольными параметрами m и σ на участок от α до β. Для вычисления этой вероятности используют общую формулу:

P (α < X < β) = F (β) – F (α), (5.39)

где F (х) – функция распределения величины Х.

С помощью математических преобразований получаем, что:

где 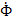— интеграл вероятностей, который рассчитывается следующим образом:

Принято называть функцию также нормальной (нормированной) функцией распре-деленияили стандартной функцией распределения.

Согласно формуле (5.39) выразим вероятность попадания СВ X на участок от α до β:

Таким образом, получили вероятность попадания на интересующий нас участок СВ X, распределенной по нормальному закону с любыми параметрами, через стандартную функцию распределения , которая соответствует простейшему нормальному законус параметрами т = 0 и σ = 1.

Заметим, что аргументы функции в формуле (5.42) имеют очень простой смысл: есть расстояние от правого конца участка до центра рассеивания, выраженное в средних квадратических отклонениях; — такое же расстояние до левого конца участка α, причем э
то расстояние считается положительным, если конец расположен справа от центра рассеивания, и отрицательным, если слева.

Date: 2016-05-25; view: 1229; Нарушение авторских прав