Закон равномерного распределения вероятностей

В задачах практики встречаются непрерывные СВ, о которых заранее известно, что их возможные значения лежат в пределах некоторого определенного интервала. Кроме того известно, что в пределах этого интервала все значения СВ обладают одной и той же плотностью вероятности. О таких случайных величинах говорят, что они распределяются по закону равной вероятностиили закону равномерной плотности. [5]

Приведем пример случайной величины, распределенной с равномерной вероятностью.

Поезда метрополитена идут с интервалом 2 мин. Пассажир выходит на платформу в некоторый момент времени. Время Т,в течение которого ему придется ждать поезда, представляет собой СВ, распределенную с равномерной плотностью на участке (0, 2) минут.

Рассмотрим СВ X, подчиненную закону равномерной плотности на участке от а до в (см. рисунок 5.6). Плотность этой величины f (x) постоянна и равна с на отрезке (а, в); вне этого отрезка она равна нулю:

(5.29)

Так как площадь, ограниченная кривой распределения, равна единице: c (в-а)=1. Отсюда получаем: c=1/(в-а).

Поэтому плотность распределения f (x) примет вид:

(5.30)

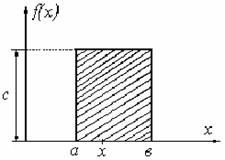
Рисунок 5.6 — График равномерной плотности распределения

Эта формула и выражает закон равномерного распределения вероятностей (закон равномерной плотности) на участке (а, в).

Напишем выражение для функции распределения F (x), которая выражается площадью, ограниченной кривой распределения и осью абсциссы, лежащей левее точки х (рисунок 5.6):

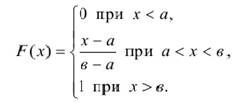(5.31)

График функции распределения F (x) приведен на рисунке 5.7.

Основные числовые характеристики СВ X на участке от а до в:

— математическое ожидание величины X:

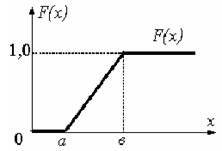
Рисунок 5.7 — Функция распределения

— дисперсия величины X:

— среднее квадратическое отклонение:

Найдем вероятность попадания СВ X распределенной по закону равномерной плотности, на участок (х 1, х 2), представляющий собой часть участка (а, в) (рисунок 5.8).

Рисунок 5.8 — Вероятность попадания величины X на участок(х 1, х 2)

Геометрически, как это видно из рисунка 5.8, вероятность представляет собой заштрихованную площадь и равна:

Date: 2016-05-25; view: 458; Нарушение авторских прав