
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Уравнения установившегося режима электрической сети
|
|
Установившимся режимом работы электрической сети при постоянных источниках тока и напряжения называется такое её состояние, при котором ток в любой ветви и напряжение в любом узле остаются относительно неизменны-ми в течение сколь угодно длительного времени.
Рассмотрим узел электрической сети, в котором соединены несколько ветвей. В качестве ветвей могут быть участки ЛЭП, трансформаторы, батареи статических конденсаторов (БСК), синхронные компенсаторы (СК) и другие элементы электрической сети.



1,2,3,…,j – номера узлов, имеющих электрическую связь с рассматриваемым
узлом I;
yi1,yi2,…,yij – продольные проводимости элементов сети
 ;
;
yi0 – проводимость i - го узла, включающая проводимости (поперечные)
элементов, установленных в i – м узле (БСК, СК, реакторы, и другие
элементы), половины поперечных проводимостей линий, подключен-
ных в i – м узле, поперечные проводимости трансформаторов (если
они примыкают к этому узлу узлом начала схемы замещения).
Например:

 .
.
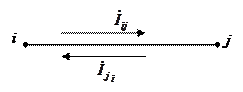
 - токи в ветвях, примыкающих и к рассматриваемому узлу. В зависимости от направления тока устанавливается знак " + " или " - ", если ток
- токи в ветвях, примыкающих и к рассматриваемому узлу. В зависимости от направления тока устанавливается знак " + " или " - ", если ток  , то противоположный ему ток
, то противоположный ему ток 
Расчетное направление тока или мощности может не совпадать с реальным.
В этом случае они будут отличаться знаками.
В соответствии с I - законом Кирхгофа в узле i должен соблюдаться баланс токов, то есть сумма токов в ветвях, присоединенных к узлу (с учетом направ-лений токов) должна быть равна инъекции тока в узле:
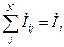 (1)
(1)
N – количество узлов непосредственно связанных с i – м узлом.
Инъекцию тока в узле І i можно определить:
 (2)
(2)
Левая часть уравнения выражения (1):
 (3)
(3)
Объединим выражения (2) и (3), и запишем формулу (1):
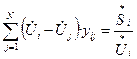 (4)
(4)
Умножим обе части уравнения (4) на  :
:
 (5)
(5)
Рассмотрим левую часть уравнения (4). Запишем баланс токов в i – м узле в развернутом виде:
 (6)
(6)
Раскроем скобки:
 (7)
(7)
Сгруппируем элементы в левой части:
 (8)
(8)
yij – взаимная проводимость узлов i и j. Равна продольной проводимости участка i – j: yij = 1 / Zij.
 - собственная проводимость узла. Равна сумме проводи-мостей всех участков, присоединенных к i – му узлу:
- собственная проводимость узла. Равна сумме проводи-мостей всех участков, присоединенных к i – му узлу:
Yii = S yij + yi0;
Во вторых скобках – сумма произведений напряжений узлов, соединенных с i – м, на их взаимные проводимости.
Запишем уравнение (8) с учетом принятых обозначений:
 Это уравнение установившегося режи-ма в форме баланса токов.
Это уравнение установившегося режи-ма в форме баланса токов.
(9) Оно описывает режим i - го узла и
баланс токов в нём.
Неизвестным являются напряжения узлов:  - напряжение рассматрива-емого узла,
- напряжение рассматрива-емого узла,  - напряжение в узлах, непосредственно связанных с i – м узлом.
- напряжение в узлах, непосредственно связанных с i – м узлом.
Заданные величины: инъекция тока  . Известными являются: собственная проводимость узла
. Известными являются: собственная проводимость узла  , взаимная проводимость
, взаимная проводимость  . Уравнение (9) линейно относительно неизвестных напряжений в узлах.
. Уравнение (9) линейно относительно неизвестных напряжений в узлах.
Подставим в правую часть формулы (9) формулу (2):
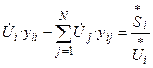 (10)
(10)
Умножим обе части уравнения (10) на  :
:
 .
.
Получаем уравнение установившегося режима в форме баланса мощности:

(11)
Описывает баланс мощностей в i – м узле.
 - сопряженный комплекс мощности, заданной в i – м узле.
- сопряженный комплекс мощности, заданной в i – м узле.
Неизвестные величины: напряжения в узлах  .
.
Известные величины:  .
.
Уравнение (11) - нелинейное относительно неизвестных напряжений.
Примечания:
1. Уравнения (9) и (11) – уравнения с комплексными неизвестными и
комплексными неизвестными. Содержат параметры, характеризую-
щие схему сети (проводимости yii и yij) и её режим (напряжения Ui
и Uj, мощности Si, Pi, Qi);
2. Неизвестными величинами в них являются напряжения узлов Ui и Uj;
3. Известные величины в них – собственная и взаимные проводимости
узлов. Заданные величины – ток и мощность в узле;
4. Уравнения записаны для одного узла электрической сети. Для схемы,
состоящей из N узлов, потребуется записать систему из N таких
уравнений.
Лекция 8
В практических расчетах комплексные уравнения (9) и (11) часто исполь-зуются в преобразованном виде. Комплексные величины в их составе пред-ставляются в виде действительных и мнимых составляющих. В результате, комплексное уравнение распадается на два действительных уравнения.
Преобразуем уравнение (11), представив неизвестные напряжения (комп-лексные величины) Ui,Uj в прямоугольных координатах:

Проводимости тоже представим в виде составляющих:
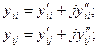 (12)
(12)
Мощность:  ;
;
Подставим эти значения в (11):

Выполняем преобразование: раскрываем скобки, группируем, разделяем действительную и мнимую части уравнения. Получаем два действительных
уравнения установившегося режима в форме баланса мощностей, записанных в прямоугольных координатах:
 (13)
(13)
Неизвестные величины в них - составляющие напряжений Ui’, Ui”, Uj’, Uj”.
Уравнение (13) описывает баланс активной и реактивной мощности в одном i – м узле сети. Для сети, состоящей из n узлов нужно записать 2n таких урав-нений. Неизвестными являются составляющие напряжения 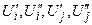 .
.
Представим уравнение (11) в полярных координатах. Для этого комплексы неизвестных напряжений запишем в соответствии с формулой Эйлера:
 .
.
Здесь Ui – модуль, 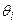 - фаза напряжения.
- фаза напряжения.
 |
 (14)
(14)
Подставим (14) в (11) учетом того, что
 (15)
(15)
Преобразуем уравнение (15): раскрываем скобки, группируем, разделя-ем действительные и мнимые части, меняем местами 
 (16)
(16)
Это уравнение установившегося режима в форме баланса мощности,
записанное в полярных координатах. Неизвестные величины в нём - модули напряжений 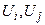 и фазы напряжений
и фазы напряжений 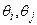 .
.
Это два действительных уравнения, записанные для одного i -го узла схемы. Определяют баланс активной и реактивной мощности в нем.
Существуют и другие формы записи уравнений установившегося режима.
Пример:

Составить уравнения в форме баланса токов для каждого из узлов сети

Составим уравнение для первого узла.
Для него i=1; j=0,2,3; n=3;

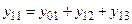 - собственная проводимость 1 – го узла.
- собственная проводимость 1 – го узла.
Для узла 0: i=0; j=1; n=1;

Для узла 2: i=2; j=1,3; n=2;

Для узла 3: i=3; j=1,2; n=2;

Уравнения в форме баланса мощностей можно получить, если умножить каждое из полученных уравнений на сопряженный комплекс соответствующе-го напряжения.
Запишем уравнение для 1 – го узла в прямоугольных координатах:

Для узлов 2 и 3 уравнения в прямоугольных координатах записать самостоятельно.
Уравнения для 1-го узла в полярных координатах:
i=1; j=0,2,3; n=3;
Используем формулу (16):
Date: 2016-05-25; view: 494; Нарушение авторских прав