
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Резонанс напряжений в цепи переменного тока
|
|
Индуктивное и емкостное сопротивления, соединенные последовательно, вызывают в цепи переменного тока меньший сдвиг фаз между током и напряжением, чем если бы они были включены в цепь по отдельности.
Иначе говоря, от одновременного действия этих двух различных по своему характеру реактивных сопротивлений в цепи происходит компенсация (взаимное уничтожение) сдвига фаз.
Полная компенсация, т. е. полное уничтожение сдвига фаз между током и напряжением в такой цепи, наступит тогда, когда индуктивное сопротивление окажется равным емкостному сопротивлению цепи, т. е. когда XL = ХС или, что то же, когда?L = 1 /?С.
Цепь в этом случае будет вести себя как чисто активное сопротивление, т. е. как будто в ней нет ни катушки, ни конденсатора. Величина этого сопротивления определится суммой активных сопротивлений катушки и соединительных проводов. При этом действующее значение тока в цепи будет наибольшим и определится формулой закона Ома I = U / R, где вместо Z теперь поставлено R.
Одновременно с этим действующие напряжения как на катушке UL = IXL так и на конденсаторе Uc = IХС окажутся равными и будут максимально большой величины. При малом активном сопротивлении цепи эти напряжения могут во много раз превысить общее напряжение U на зажимах цепи. Это интересное явление называется в электротехнике резонансом напряжений.
На рис. 1 приведены кривые напряжений, тока и мощности при резонансе напряжений в цепи.
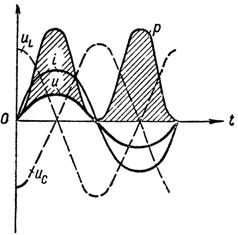
График тока напряжений и мощности при резонансе напряжений
Следует твердо помнить, что сопротивления XL и ХС являются переменными, зависящими от частоты тока, и стоит хотя бы немного изменить частоту его, например, увеличить, как XL =?L возрастет, а ХС = = 1 /?С уменьшится, и тем самым в цепи сразу нарушится резонанс напряжений, при этом наряду с активным сопротивлением в цепи появится и реактивное. То же самое произойдет, если изменить величину индуктивности или емкости цепи.
При резонансе напряжений мощность источника тока будет затрачиваться только на преодоление активного сопротивления цепи, т. е. на нагрев проводников.
Действительно, в цепи с одной катушкой индуктивности происходит колебание энергии, т. е. периодический переход энергии из генератора в магнитное поле катушки. В цепи с конденсатором происходит то же самое, но за счет энергии электрического поля конденсатора. В цепи же с конденсатором и катушкой индуктивности при резонансе напряжений (XL = ХС) энергия, раз запасенная цепью, периодически переходит из катушки в конденсатор и обратно и на долю источника тока выпадает только расход энергии, необходимый для преодоления активного сопротивления цепи. Таким образом, обмен энергии происходит между конденсатором и катушкой почти без участия генератора.
Стоит только нарушить резонанс напряжений в цени, как энергия магнитного поля катушки станет не равной энергии электрического поля конденсатора, и в процессе обмена энергии между этими полями появится избыток энергии, который периодически будет то поступать из источника в цепь, то возвращаться ему обратно цепью.
Явление это очень сходно с тем, что происходит в часовом механизме. Маятник часов мог бы непрерывно колебаться и без помощи пружины (или груза в часах-ходиках), если бы не силы трения, тормозящие его движение.
Пружина же, сообщая маятнику в нужный момент часть своей энергии, помогает ему преодолеть силы трения, чем и достигается непрерывность колебаний.
Подобно этому и в электрической цепи, при явлении резонанса в ней, источник тока расходует свою энергию только на преодоление активного сопротивления цепи, тем самым поддерживая в ней колебательный процесс.
Итак, мы приходим к выводу, что цепь переменного тока, состоящая из генератора и последовательно соединенных катушки индуктивности и конденсатора, при определенных условиях XL = ХС превращается в колебательную систему. Такая цепь получила название колебательного контура.
Из равенства XL = ХС можно определить значения частоты генератора, при которой наступает явление резонанса напряжений:

Значение емкости и индуктивности цепи, при которых наступает резонанс напряжений:
Lрез = 1 /?2С, Срез = 1 /?2L
Таким образом, изменяя любую из этих трех величин (fрез, L и С), можно вызвать в цепи резонанс напряжений, т. е. превратить цепь в колебательный контур. 
Пример полезного применения резонанса напряжений: входной контур приемника настраивается конденсатором переменной емкости (или вариометром) таким образом, что в нем возникает резонанс напряжений. Этим достигается необходимое для нормальной работы приемника большое повышение напряжения на катушке по сравнению с напряжением в цепи, созданным антенной.
Наряду с полезным использованием явления резонанса напряжений в электротехнике технике часто бывают случаи, когда резонанс напряжений вреден. Большое повышение  _ напряжения на отдельных участках цепи (на катушке или на конденсаторе) по сравнению с напряжением генератора может привести к порче отдельных деталей и измерительных приборов.
_ напряжения на отдельных участках цепи (на катушке или на конденсаторе) по сравнению с напряжением генератора может привести к порче отдельных деталей и измерительных приборов.
Векторные диаграммы
В цепях переменного тока все токи и напряжения являются синусоидальными функциями времени. Поэтому аналитические зависимости в виде уравнений не дают представления о реальных соотношениях величин. При переходе от оригиналов функций и параметров к их изображениям в виде комплексных чисел задача анализа несущественно упрощается, т.к., в отличие от цепей постоянного тока, где все величины однозначно характеризуются одним числом, в области изображений каждая величина определяется двумя числами, каждое из которых в общем случае недостаточно для полной оценки состояния цепи. Помочь в анализе соотношений между величинами и параметрами электрический цепи может их геометрическое представление в виде векторной диаграммы.
Из курса математики известно, что любое комплексное число может быть изображено в виде точки на плоскости с ортогональной системой координат, в которой на оси абсцисс откладывается вещественная составляющая, а на оси ординат мнимая. Такое изображение соответствует алгебраической форме записи комплексного числа. Если начало координат соединить отрезком прямой с точкой изображающей комплексное число, то длина этого отрезка и его угол с вещественной осью также могут служить изображением комплексного числа. Причем, для однозначного определения угла нужно задать положительное направление отрезка, т.е. определить его как радиус-векторили просто вектор.
Векторной диаграммой называется совокупность векторов на комплексной плоскости, соответствующая комплексным величинам и/или параметрам электрической цепи и их связям.
Векторные диаграммы могут быть точными и качественными. Точные диаграммы строятся с соблюдением масштабов всех величин по результатам численного анализа. Они предназначены в основном для проверки расчетов. Качественные векторные диаграммы строятся с учетом взаимных связей между величинами и обычно предшествуют расчету или заменяют его. В качественных диаграммах масштаб изображения и конкретные значения величин несущественны, важно только, чтобы в них были правильно отражены все связи между величинами, соответствующие связям и параметрам элементов электрической цепи. Качественные диаграммы являются важнейшим инструментом анализа цепей переменного тока.
В цепях переменного тока одной из самых распространенных задач является анализ поведения цепи при изменении в широких пределах какой-либо величины или параметра.

Пусть, например, требуется исследовать изменение тока в цепи, представленной на рис. 1 а), при постоянном напряжении на входе и изменении резистивного сопротивления в пределах 0 > R > µ.
Падение напряжения на входе уравновешивается суммой падений напряжения на R и L, т.е. u = uR + uL = Ri + Ldi / dt или для изображений
| U = U R + U L = R I + jw L I = R I + jXL I. | (1) |
Из выражения (1) следует, что
- векторы U R и U L всегда перпендикулярны друг другу, т.к. каждый из них представляет собой вектор тока I, умноженный на соответствующую константу (R или XL), а в падении напряжения U L присутствует в качестве множителя оператор поворота на 90° - j;
- сумма векторов U R и U L постоянная и равна вектору U.
Для упрощения построений, не ограничивая в то же время общности рассуждений, совместим вектор U с вещественной осью (рис. 1 б)). Тогда в соответствии с условиями (1) при любых значениях R векторы U R и U L будут составлять с вектором U прямоугольные треугольники. Как известно, любой треугольник может быть вписан в окружность, причем дуги, на которые опираются углы вписанного треугольника равны двойному значению угла. Так как во всех векторных треугольниках угол между U R и U L равен 90°, то все они опираются на дугу в 180°, т.е. на диаметр, которым является постоянный вектор входного напряжения U. Следовательно, все треугольники векторов U R, U L и U вписываются в одну и ту же полуокружность, которая является геометрическим местом точек перемещения конца вектора U R при всех изменениях значения R.
Векторная диаграмма, в которой при вариации параметров геометрическим местом точек перемещения конца какого-либо вектора является окружность или полуокружность, называется круговой диаграммой.
Так как векторы U R и U L связаны с вектором тока I постоянными коэффициентами, то из круговой диаграммы вектора U R можно получить векторную диаграмму тока и она также будет круговой. Для получения вектора I, в соответствии с выражением (1), достаточно разделить все элементы треугольников U R, U L и U на R или jXL. При этом мы получим подобный треугольник, одним из катетов которого будет I. Однако деление на R нецелесообразно, т.к. эта величина переменная и для сохранения масштаба треугольников следует произвести деление на jXL. В результате диаметр полуокружности станет равным U / XL и она вследствие деления на оператор поворота j повернется относительно начала координат на угол - 90° (рис. 1 в)). Полученная полуокружность и будет круговой диаграммой вектора входного тока I. Из нее можно заключить, что при R = 0 вектор тока отстает от напряжения на 90° и по модулю равен U / XL. При R ® µ модуль и аргумент вектора тока стремятся к нулю.
Другой важной разновидностью векторных диаграмм являются линейные диаграммы.
Линейной диаграммой называется векторная диаграмма, в которой геометрическим местом точек конца какого-либо вектора при вариации параметра является прямая линия.
 Примером такой диаграммы может служить диаграмма входного тока I пассивного двухполюсника при постоянном напряжении на входе U =const и изменении его реактивной проводимости в пределах - µ > B > +µ, если активная составляющая проводимости G остается постоянной. Примером электрической цепи с такой вариацией реактивной проводимости является параллельный резонансный контур при вариации частоты 0 < w <µ.
Примером такой диаграммы может служить диаграмма входного тока I пассивного двухполюсника при постоянном напряжении на входе U =const и изменении его реактивной проводимости в пределах - µ > B > +µ, если активная составляющая проводимости G остается постоянной. Примером электрической цепи с такой вариацией реактивной проводимости является параллельный резонансный контур при вариации частоты 0 < w <µ.
Действительно, активная составляющая тока любого двухполюсника равна I а= G U, а реактивная I р= jB U, т.е. эти составляющие всегда перпендикулярны друг другу или, иначе говоря, находятся в квадратуре, т.к. являются производными от одного и того же вектора U, но I р содержит оператор поворота на 90° - j. Входной ток представляет собой сумму активной и реактивной составляющих I = I а+ I р, причем, активная составляющая отличается от вектора U постоянным вещественным множителем G, поэтому всегда совпадает с ним по фазе (рис. 2 б)) и имеет постоянный модуль. Вектор реактивной составляющей имеет переменный модуль - µ < | I р| < + µ и I а ^ I р, следовательно, он будет располагаться на прямой проходящей через начало координат перпендикулярно вектору U. Поэтому суммарный вектор входного тока I при изменении реактивной проводимости будет скользить своим концом по линии перпендикулярной векторам I а и U и проходящей через конец вектора I а.
Для качественного анализа электромагнитных процессов в электрической цепи переменного тока можно строить векторные диаграммы, пользуясь только принципиальной схемой.
 Построим качественную векторную диаграмму для цепи рис. 3.
Построим качественную векторную диаграмму для цепи рис. 3.
Построение всегда можно начинать с произвольно выбранной величины, но т.к. операции суммирования векторов производятся проще, чем операции разложения на составляющие, то лучше в качестве начального вектора выбирать напряжение или ток элемента цепи, расположенного как можно дальше от входа. Тогда входные величины будут получены постепенным сложением векторов.
Пусть вектор тока I 5 расположен так, как это показано на рис. 3. Ток I 5 протекает в емкости C 2, подключенной к узлам b и c цепи. Поэтому U bc = U C 2. Но падение напряжения на емкости отстает от тока в ней на 90°, следовательно, U bc нужно расположить на луче перпендикулярном вектору I 5 и смещенном в сторону отставания, т.е. по часовой стрелке.
Между узлами b и c помимо емкости C 2 включена ветвь, содержащая резистор r и индуктивность L. Ток в активно-резистивном двухполюснике отстает от напряжения на некоторый угол φ, конкретное значение которого определяется отношением индуктивного сопротивления w L к резистивному r. Поэтому конец вектора тока I 4 в r - L ветви рис. 3 может находиться в любой точке сектора комплексной плоскости в 90°, ограниченного лучом совпадающим по направлению с U bc и перпендикулярным ему лучом, смещенным в сторону отставания. Зададим произвольно точку конца вектора I 4 в этом секторе. Тогда падение напряжения на резисторе r должно совпадать по направлению с I 4, а падение напряжение на индуктивности L - опережать I 4 на 90°, причем в сумме U r и U L должны быть равны U bc. Построение векторов U r и U L, удовлетворяющих этим условиям, проще всего произвести проектированием конца вектора U bc на направление вектора I 4. Тогда вектор, совпадающий с I 4 по направлению, будет U r, а перпендикулярный ему - U L.
Уравнение Кирхгофа для узла b цепи можно записать в виде I 3 = I 4 + I 5, поэтому сложение векторов I 4 и I 5 по правилу параллелограмма даст нам вектор тока I 3, протекающего в резисторе R рис. 3. Падение напряжения на нем U R = U ab, как у любого резистора, будет совпадать по фазе с током, следовательно, его можно построить на луче совпадающем по направлению с I 3.
По второму закону Кирхгофа разность потенциалов U ac можно представить суммой U ac = U ab + U bc = U. Соответственно, вектор входного напряжения U получается сложением по правилу параллелограмма векторов U ab и U bc рис. 3. Но U ac = U С1. Следовательно, ток в емкости C 1 должен опережать напряжение U ac на 90°, поэтому его нужно построить на луче перпендикулярном U ac и смещенном в сторону опережения.
Для узла a цепи справедливо I 1 = I 2 + I 3. В соответствии с этим равенством входной ток I 1 получен геометрическим суммированием векторов I 2 и I 3.
УРОК №36
КОНТРОЛЬНАЯ РАБОТА
Вопросы:
| 1. Электрические цепи переменного тока. |
| 2. Однофазные электрические цепи синусоидального переменного тока. |
| 3. Классификация электрических цепей переменного тока. |
| 4. Параметры и форма представления переменного тока и напряжения. |
| 5. Активное и реактивное сопротивления: временные и векторные диаграммы токов и напряжения. |
| 6. Последовательное и параллельное соединения элементов. |
| 7. Понятие о полном сопротивлении и проводимости. |
| 8. Активная, реактивная и полная мощность в цепях переменного тока. |
| 9. Коэффициент мощности и способы его повышения. |
| 10. Резонанс напряжений и токов в цепи переменного тока. Векторные диаграммы, частотные и энергетические характеристики. Понятие о расчёте сложных цепей. |
УРОК №37
Date: 2016-05-25; view: 1711; Нарушение авторских прав