
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

при помощи математического маятника
|
|
Элементарная физика
Лабораторная работа № 2
Определение ускорения свободного падения
при помощи математического маятника
Ульяновск, 2012
Цели работы: 1. определить ускорение свободного падения;
2. закрепить умения рассчитывать погрешности прямых и косвенных измерений.
Приборы и принадлежности: 1. математический маятник
2. секундомер
3. треугольник
Краткая теория
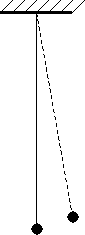 Математическим маятником называется материальная точка, подвешенная на невесомой нерастяжимой нити. Практически маятник представляет собой тяжелый шарик, линейные размеры которого малы по сравнению с длиной подвеса (нити).
Математическим маятником называется материальная точка, подвешенная на невесомой нерастяжимой нити. Практически маятник представляет собой тяжелый шарик, линейные размеры которого малы по сравнению с длиной подвеса (нити).
Период колебаний маятника при малых отклонениях определяется формулой:
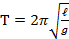 , где ℓ - длина маятника.
, где ℓ - длина маятника.
Из этой формулы выразим ускорение свободного падения
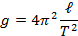
Методика проведения эксперимента
Непосредственное измерение длины математического маятника неудобно и связано со значительными погрешностями, т.к. приходится определять положение центра тяжести маятника и точки подвеса. Поэтому поступают так:
если определить период колебаний математического маятника Т1 при длине ℓ 1, а затем удлинить нить и снова определить период колебаний Т2 при длине ℓ2, то можно найти ускорение свободного падения следующим образом:

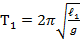 (1),
(1), 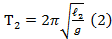 , возведем уравнения в квадрат и вычтем из уравнения (2) уравнение (1):
, возведем уравнения в квадрат и вычтем из уравнения (2) уравнение (1):
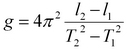
 Выразим из предыдущего равенства g:
Выразим из предыдущего равенства g:
Из рисунка следует, что расстояние между центрами тяжести шарика ℓ2 - ℓ1 в первом и втором случаях можно заменить расстоянием Z2 - Z1 от нижней части шарика в первом опыте до нижней части шарика во втором опыте.

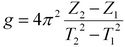 Тогда расчетная формула для определения ускорения свободного падения с помощью математического маятника будет иметь вид:
Тогда расчетная формула для определения ускорения свободного падения с помощью математического маятника будет иметь вид:
Описание экспериментальной установки
Маятник, применяемый в данной работе, представляет собой металлический шарик, подвешенный на бифилярном подвесе, длина которого изменяется с помощью маховичка, укрепленного на кронштейне. Треугольник служит для определения положения нижней точки маятника относительно вертикальной шкалы.
Порядок выполнения работы
1. Установить длину маятника ℓ1.
2. Приложить один катет треугольника к шкале так, чтобы он другим катетом касался шарика. Отсчитать по шкале с точностью до 1 мм положение нижней части шарика (Z1).
3. Отклонить маятник на небольшой угол (не более 50). Измерить секундомером время t1, в течение которого совершается полных 50 колебаний.
4. Найти период колебаний маятника по формуле 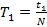 .
.
5. При данной длине измерение повторить 5 раз.
6. Найти среднее значение Т1ср.
7. Вычислить погрешности. Заполнить таблицу 1.
Таблица 1
| t1i, с | ∆t1i, с |  , с , с
| ∆t1 при a = | εt, % | Т1, с | ∆Т1, с | εТ, % | |
| СЗ |
8. Установить другую длину маятника ℓ2. Разность длин должна быть значительной (не менее 50 см), т.к. при малой разности длин мала и разность квадратов периодов, что приводит к большой погрешности определения ускорения свободного падения.
9. Повторить пункты 2-7 для длины ℓ2. Заполнить таблицу 2.
Таблица 2
| t2i, с | ∆t2i, с | 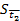 , с , с
| ∆t2 при a = | εt, % | Т2, с | ∆Т2, с | εТ, % | |
| СЗ |
10. Заполнить таблицу 3.
Таблица 3
| ℓ2 - ℓ1, см | Т12, с2 | Т22, с2 | g, м/с2 | εg, % | ∆g, м/с2 | g + ∆g, м/с2 |
11. Сделайте вывод.
Контрольные вопросы
1. Что называется математическим маятником?
2. Вывести формулу периода колебаний математического маятника.
3. При каких условиях колебания математического маятника будут гармоническими?
4. К каким измерениям относится измерение ускорения свободного падения?
5. Как определить относительную погрешность измерения ускорения свободного падения?
6. Что такое относительная погрешность измерения? Способы ее определения.
7. Физический смысл коэффициента Стьюдента.
| <== предыдущая | | | следующая ==> |
| Особенности профессионально-этического сознания социального работника | | | Методика обучения как наука. Объект и предмет методики. Связь методики с другими науками |
Date: 2016-05-24; view: 721; Нарушение авторских прав