
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод расчета пластины в балочных функциях
|
|
1.1. Основы метода. Рассмотрим пластину в декартовой системе координат (рис.).
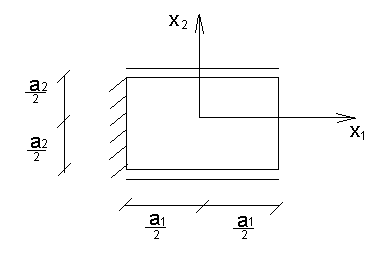
К расчету данной пластины по классической теории используем следующий метод, который реализуется в следующей последовательности.
1.Функция прогибов (W)
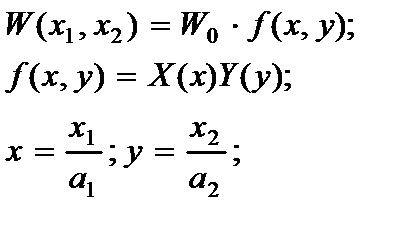 (2.127)
(2.127)
где W 0 - максимальный прогиб; X(x), Y(y) - нормированные балочные безразмерные функции; x, y - безразмерные координаты.
2.Углы поворотов пластины (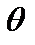 1,
1, 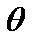 2).
2).
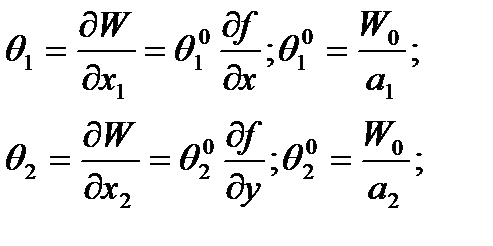 (2.128)
(2.128)
3.Кривизны 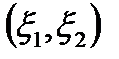 и кручение
и кручение 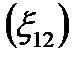 .
.
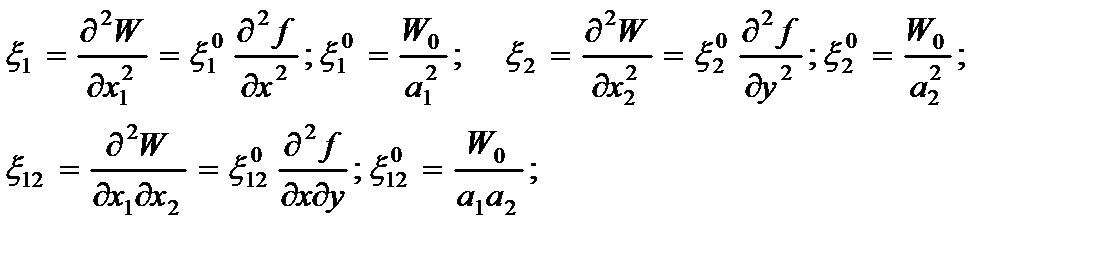 (2.129)
(2.129)
4. Изгибающие (M1,M2) и крутящий (M12) моменты.
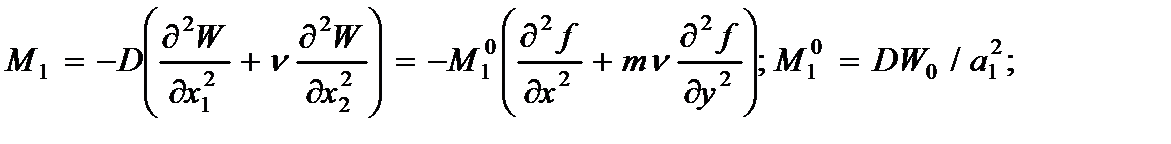
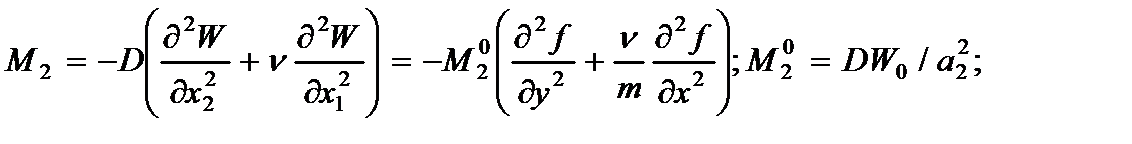 (2.130)
(2.130)
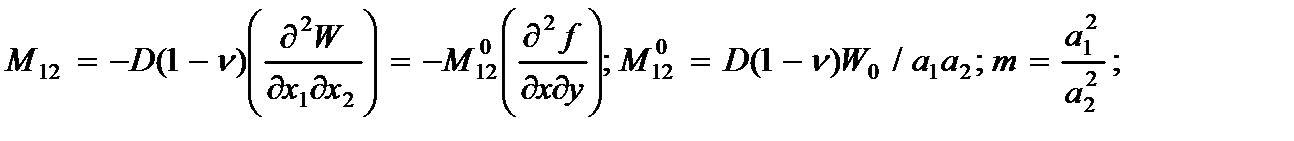 где D – цилиндрическая жесткость пластины,
где D – цилиндрическая жесткость пластины, 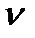 - коэффициент Пуассона, m - отношения квадрат сторон пластины.
- коэффициент Пуассона, m - отношения квадрат сторон пластины.
5. Поперечные силы (Q1,Q2).
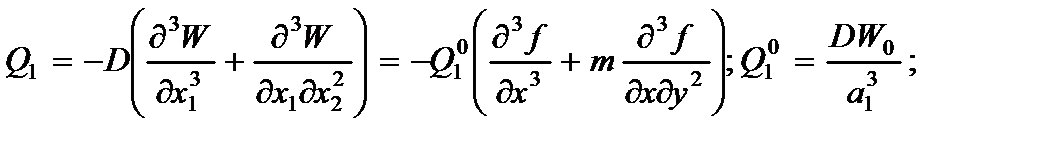
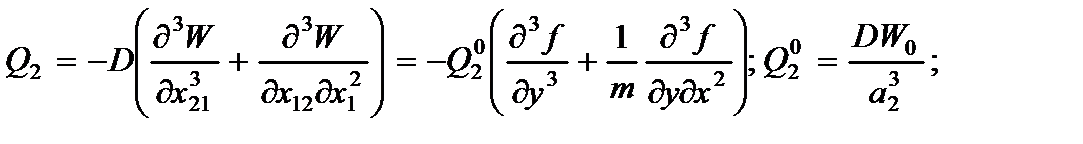 (2.131)
(2.131)
6. Интенсивность внутренних усилий (P).
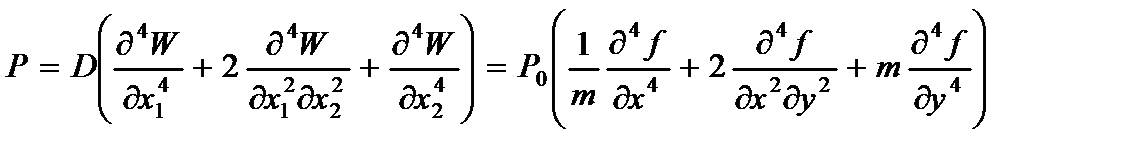 ;
; 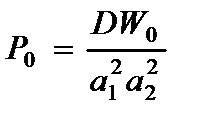 (2.132)
(2.132)
7. Основное уравнение равновесия пластины
а) в размерных координатах:
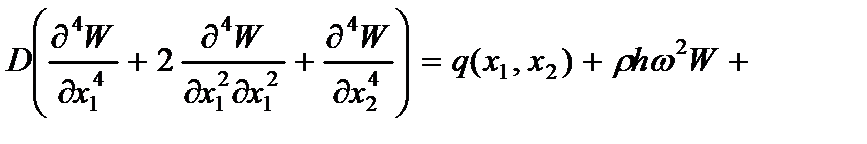
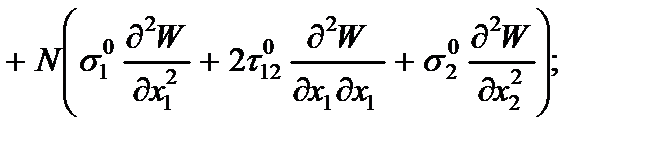 (2.133)
(2.133)
б) в безразмерных координатах:
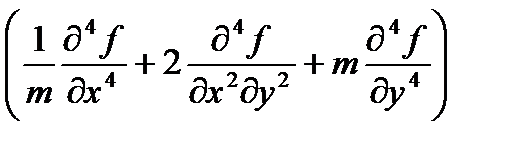
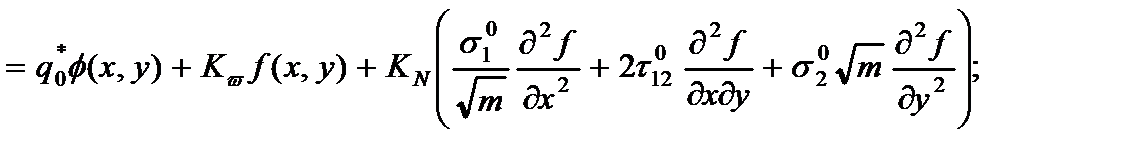
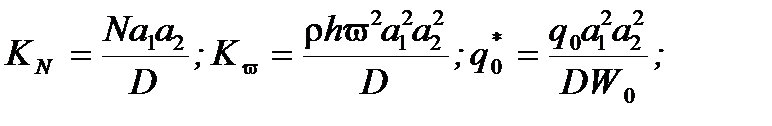 (2.134)
(2.134)
где KN – параметр критической нагрузки, 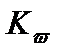 - частотный параметр свободных колебаний, q*0 - параметр нагрузки, S(x,y) -закон изменения интенсивности внутренних усилий, V(x,y) - закон изменения интенсивности внутренних усилий от мембранных напряжений;
- частотный параметр свободных колебаний, q*0 - параметр нагрузки, S(x,y) -закон изменения интенсивности внутренних усилий, V(x,y) - закон изменения интенсивности внутренних усилий от мембранных напряжений;  - закон изменения мембранных напряжений;
- закон изменения мембранных напряжений; 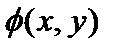 - закон изменения интенсивности внешней поперечной распределенной нагрузки.
- закон изменения интенсивности внешней поперечной распределенной нагрузки.
8. Выполнение уравнения равновесия пластины осуществляется:
а) при равенстве работ:
 (2.135)
(2.135)
б) при равенстве равнодействующих:
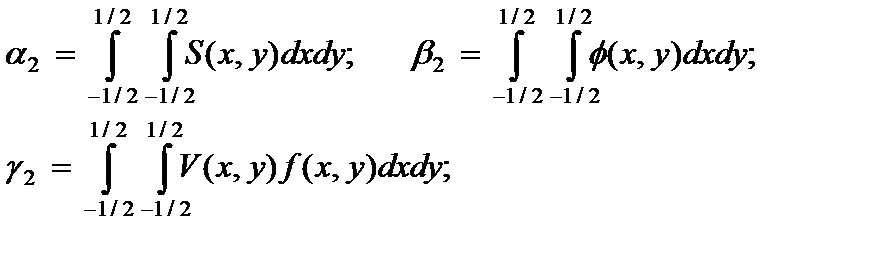 (2.136)
(2.136)
в) при равенстве интенсивностей:

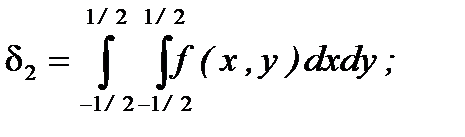
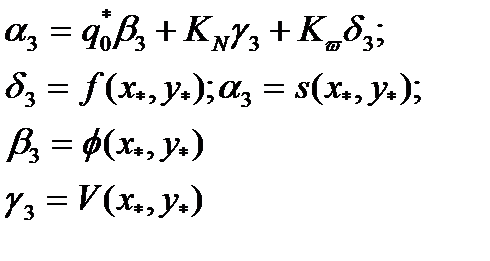 (2.137)
(2.137)
где – 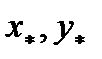 безразмерные координаты пластины в характерной точке
безразмерные координаты пластины в характерной точке
9. граничные (контурные) условия пластины при изгибе для края x1=x1*=const.
а) шарнирно опертого:
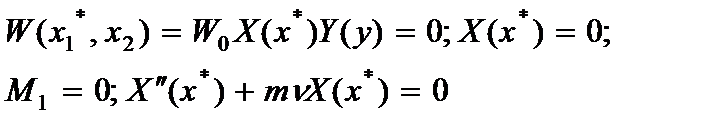 (2.138)
(2.138)
б) защемленного:
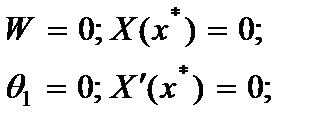 (2.139)
(2.139)
в) свободного:
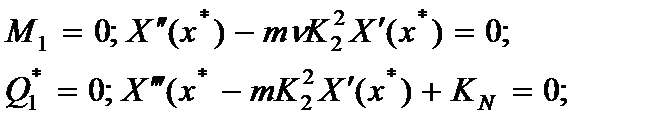 (2.140)
(2.140)
где K2 - собственное число уравнения 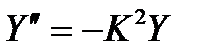
Второе условие при решении задачи устойчивости запишутся так:
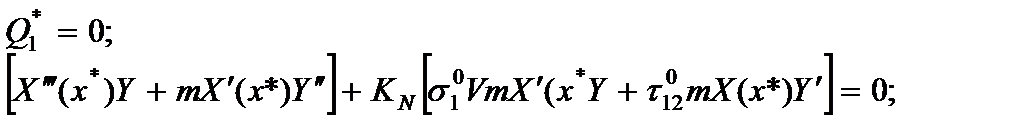 (2.141)
(2.141)
10. основные задачи пластины имеют решения
а) при изгибе 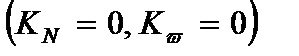
б) при устойчивости 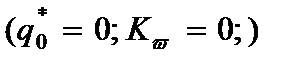 (2.142)
(2.142)
в) при колебаниях 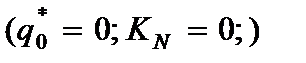
11. Погрешность предлагаемого метода вычисляются по формулам:
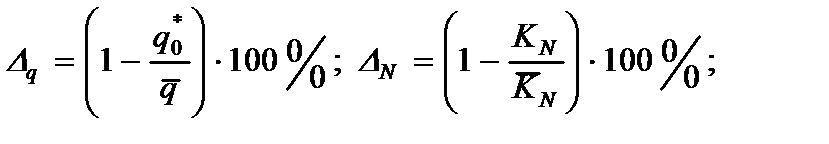
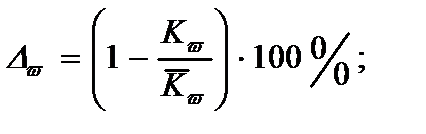 (2.143)
(2.143)
где  - точные значения параметров, q0*,KN,K
- точные значения параметров, q0*,KN,K 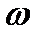 -параметры, вычисленные предложенным методом.
-параметры, вычисленные предложенным методом.
1.2 Балочные функции.
А) при изгибе под действием равномерно распределенной нагрузки
1.концы балки шарнирно оперты:
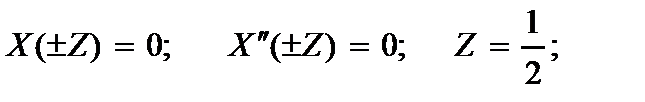
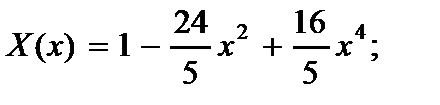 (2.144)
(2.144)
2. концы жестко защемлены:
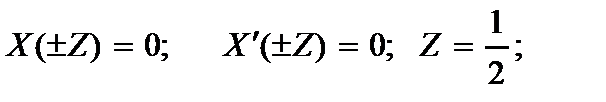
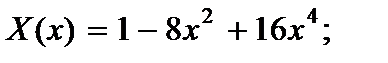 (2.145)
(2.145)
3.концы балки имеют комбинированные закрепления:
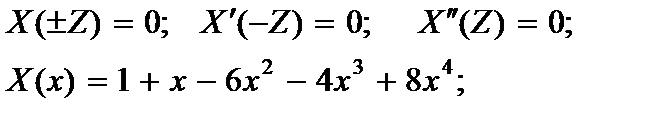 (2.146)
(2.146)
Б) При потери устойчивости
1.концы балки шарнирно оперты:
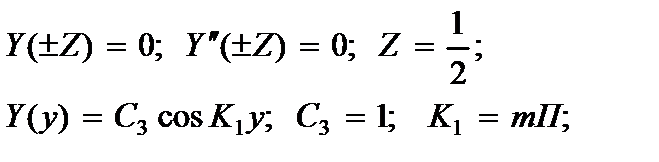 (2.147)
(2.147)
2. концы балки закреплены:
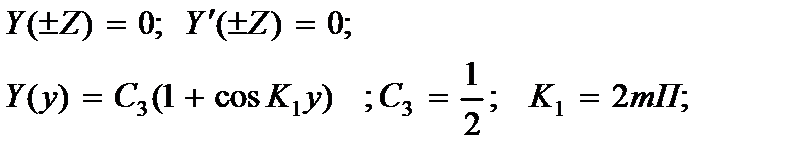 (2.148)
(2.148)
3.консольная балка:
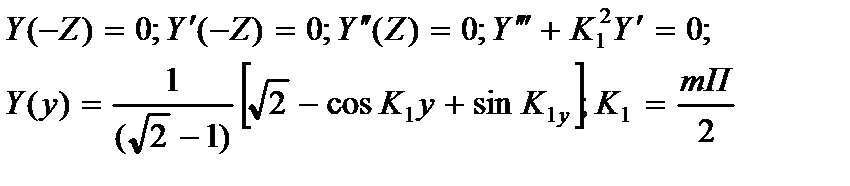 (2.149)
(2.149)
4. концы балки свободные:
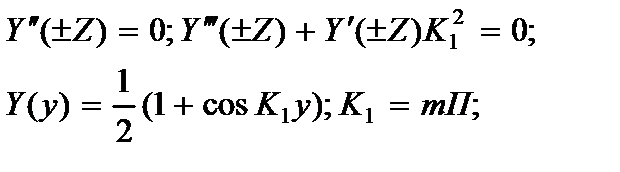 (2.150)
(2.150)
5.концы балки имеют комбинированные закрепления:
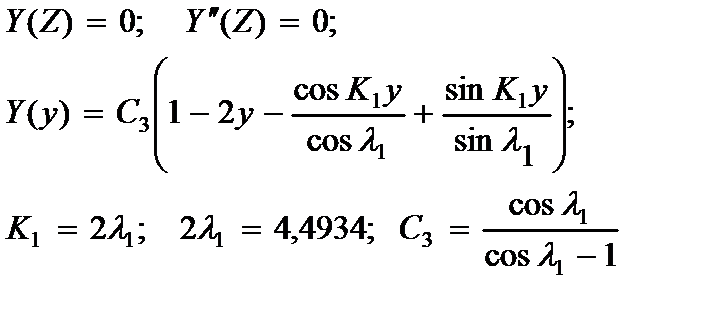 (2.151)
(2.151)
1.3. Алгоритм расчета пластины.
Расчет любой пластины производится в следующей последовательности.
1.Выбрать расчетную схему пластины в соответствии с граничными условиями.
2. В зависимости от типа задачи пластины (изгиб, устойчивость, колебания) подбираются функции согласно формулам (2.144)-(2.151). При этом при решении задач изгиба и свободных колебаний (2.144)-(2.146).
3. По условию задачи определить 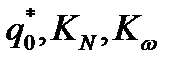 , используя (2.135)-(2.137).
, используя (2.135)-(2.137).
4. Вычислить их погрешности по 17 и сделать соответствующий вывод.
5. Результаты представить в виде эпюр используя (2.127)-(2.136).
6. Анализировать полученные результаты и сделать соответствующие выводы на основании функции прогибов 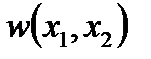 (2.127).
(2.127).
а) для задачи изгиба деформированное состояние 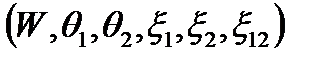 и напряженное состояние (M1,M2,M12,Q1,Q2);
и напряженное состояние (M1,M2,M12,Q1,Q2);
б) для задачи устойчивости функции прогибов (2.127) (форма потери устойчивости) и параметр нагрузки 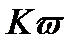 .
.
| <== предыдущая | | | следующая ==> |
| Классическая и уточненная теория изгиба прямоугольных пластин | | |
Date: 2016-05-24; view: 553; Нарушение авторских прав