Методами 1-го и 2-го порядка

1. Формирование данных о текущем состоянии приближений искомых неизвестных U^(k).

При к=0 исходные приближения неизвестных можно принять равными номинальному напряжению U⁽⁰⁾=U_ном, либо задать на основе предыдущих близких расчетов;

2. Определение невязок уравнений исходной системы при текущем значении U_k: W(U_k);

3. Проверка условий окончания расчета.

Часто эти условия формулируются следующим образом: максимальный небаланс мощности в узле (максимальная невязка уравнений) не должен превышать заданную величину точности ε: max{W(U_k)}≤ε;

4. Расчет элементов матрицы Якоби в методах 1-го порядка и расчет элементов матрицы Гессе в методах 2-го порядка: Y, H;

5. Решение линеаризованной системы (23) в методах 1-го порядка или решение системы квадратичных уравнений (25) в методах 2-го порядка. В результате определяются поправки к неизвестным ∆U^(к);

6. Определение очередного приближения неизвестных

7. Возврат к пункту 1.

Таким образом, порядок методов расчета режимов определяется старшей производной из используемых в рекуррентных выражениях итерационного процесса.

Методы нулевого порядка обходятся без вычисления производных (метод простых итераций, метод Зейделя).

В методах 1-го порядка используется 1-я производная от уравнений установившегося режима (матрица Якоби в методе Ньютона-Рафсона).

В методах 2-го порядка используется 2-я производная (матрица Гессе). Это современные методы, обеспечивающие быструю сходимость и высокую надежность в получении результата.

Методы 3-го порядка в настоящее время не эффективны.

Пример: Расчет режима простейшей электрической сети методом 2-го

порядка

Рассматриваем сеть постоянного тока. При этом исключаются комплексные величины, упрощаются уравнения.

Систему уравнений установившегося режима в общем виде можно записать:

. (П1)

Или в развёрнутом виде:

(П2)

Каждое уравнение системы (п2) для общего случая имеет вид:

(П3)

Для заданной схемы система уравнений установившегося режима имеет вид:

(П4)

Запишем уравнения (П4) в виде невязок:

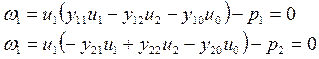(П5)

Для нахождения неизвестных напряжений U₁ и U₂ будем решать систему уравнений (П5) методом 2-го порядка.

Квадратичная аппроксимация каждого из этих уравнений выполняется в соответствии с (13):

(П6)

Уравнения (П5) могут быть апроксимированы следующим образом:

В общем виде:

.

Каждое из уравнений системы (п5):

(п7)

Уравнения системы (П7) – квадратичные уравнения с неизвестными поправками ∆U₁ и ∆U₂. Решив эту систему уравнений, определяем поправки к неизвестным и затем очередное приближение неизвестных. Система (П7) нелинейна, решается итерационными методами.

Здесь к – номер приближения искомых напряжений U₁, U₂ на внешнем итерационном цикле;

l – номер приближения поправок к неизвестным ΔU₁, ΔU₂ на внутреннем итерационном цикле решения системы квадратичных уравнений.

Запишем уравнение (П7) в соответствии с (14):

Строки полной матрицы Гессе формируются из строк матриц Н₁ и Н₂ в (п7). Определим выражения производных в составе матриц Якоби и Гессе, для этого дифференцируем уравнения системы (П5) по всем неизвестным напряжениям:

(п9)

В общем виде диагональные элементы можно записать:

Элементы матрицы Гессе получаем дифференцированием (П9):

Элементы матрицы Гессе в общем виде можно записать:

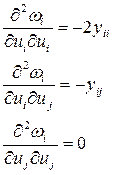(П10)

Таким образом:

(П11)

Элементы матрицы Гессе включают только собственные и взаимные проводимости, следовательно их элементы не зависят от режима и ее не нужно пересчитывать в ходе расчета, т.е. она остаётся постоянной.

Если сложить Н₁ и Н₂, то получим - удвоенная матрица проводимостей.

Матрица Гессе легко формируется из элементов матрицы проводимостей.

Подставим полученные значения производных в уравнения (п7):

(п12)

В результате дальнейших преобразований системы (П12) получаем систему 2-х квадратичных уравнений относительно поправок к неизвестным ∆U₁, ∆U₂. Ее решение возможно только итерационными методами.

Date: 2016-05-23; view: 475; Нарушение авторских прав