Физические приложения определенного интеграла

С помощью физических приложений вычисляются: работа переменной силы, давление жидкости на вертикальную пластинку, статические моменты и координаты центра тяжести плоской кривой и плоской фигуры.

1. Работа переменной силы

Пусть под действием некоторой силы материальная точка М движется по прямой в направлении оси . Требуется найти работу, произведённую силой при перемещении точки М из положения в положение .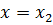

1) Если сила постоянна , то работа выражается следующим образом .

2) Если сила переменная величина, то

.

Пример.

Два электрических заряда и находятся на оси соответственно в точках 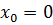и . Какая работа будет произведена, если второй заряд переместится в точку ? (Сила взаимодействия зарядов ).

Решение:

2. Давление жидкости на вертикальную пластинку

По закону Паскаля давление жидкости на горизонтальную пластину равно весу столба этой жидкости, имеющего основанием пластинку, а высотой — глубину ее погружения от свободной поверхности жидкости, т.е. , где — ускорение свободного падения, — плотность жидкости, 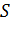– площадь пластинки, – глубина ее погружения.

По этой формуле нельзя искать давление жидкости на вертикально погруженную пластинку, так как ее разные точки лежат на разных глубинах. Пусть в жидкость погружена вертикально пластина, ограниченная линиями и ; система координат выбрана так, как указано на рисунке 11. Для нахождения давления жидкости на эту пластину применим схему II (метод дифференциала).

Рисунок 11

1. Пусть часть искомой величины есть функция от : , т.е. — давление на часть пластины, соответствующее отрезку 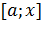значений переменной , где .

2. Дадим аргументу приращение 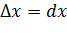. Функция получит приращение (на рисунке — полоска-слой толщины ). Найдем дифференциал этой функции. Ввиду малости будем приближенно считать полоску прямоугольником, все точки которого находятся на одной глубине , т.е. пластинка эта — горизонтальная. Тогда по закону Паскаля , где , .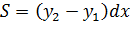

3. Интегрируя полученное равенство в пределах от до , получим:

3. Вычисление статических моментов и координат центра тяжести плоской кривой

Пусть на плоскости задана система материальных точек соответственно с массами .

Статическим моментом системы материальных точек относительно оси называется сумма произведений масс этих точек на их ординаты (т.е. на расстояния этих точек от оси ):

Аналогично определяется статический момент этой системы относительно оси :

Если массы распределены непрерывным образом вдоль некоторой кривой, то для выражения статического момента понадобится интегрирование.

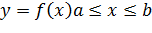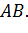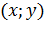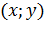Пусть — это уравнение материальной кривой Будем считать ее однородной с постоянной линейной плотностью . Для произвольного на кривой найдется точка с координатами . Выделим на кривой элементарный участок длины , содержащий точку . Тогда масса этого участка равна . Примем этот участок приближенно за точку, отстоящую от оси на расстоянии . Тогда дифференциал статического момента ("элементарный момент") будет равен 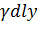, т.е. 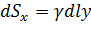(рисунок 12).

Отсюда следует, что статический момент кривой относительно оси равен:

Рисунок 12

Аналогично находим :

Статические моменты и кривой позволяют легко установить положение ее центра тяжести (центра масс).

Центром тяжести материальной плоской кривой называется точка плоскости, обладающая следующим свойством: если в этой точке сосредоточить всю массу заданной кривой, то статический момент этой точки относительно любой координатной оси будет равен статическому моменту всей кривой относительно той же оси. Обозначим через центр тяжести кривой . Из определения центра тяжести следуют равенства и или и .

Отсюда или ; .

Пример. Найти центр тяжести однородной дуги окружности

, расположенной в первой координатной четверти (рисунок 13).

Решение: Очевидно, длина указанной дуги окружности равна , т.е. .

Рисунок 13

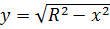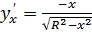Найдем статический момент ее относительно оси . Так как уравнение дуги есть и , то

Стало быть,

Так как данная дуга симметрична относительно биссектрисы первого координатного угла, то . Итак, центр тяжести имеет координаты

.

4. Вычисление статических моментов и координат центра тяжести плоской фигуры

Пусть дана материальная плоская фигура (пластинка), ограниченная кривой и прямыми (рисунок 14).

Рисунок 14

Будем считать, что поверхностная плотность пластинки постоянна . Тогда масса всей пластинки равна , т.е.

Выделим элементарный участок пластинки в виде бесконечно узкой вертикальной полосы и будем приближенно считать его прямоугольником. Тогда масса его равна . Центр тяжести прямоугольника лежит на пересечении диагоналей прямоугольника. Эта точка отстоит от оси на , а от оси на (приближенно; точнее на расстоянии ). Тогда для элементарных статических моментов относительно осей и выполнены соотношения

и

Следовательно,

По аналогии с плоской кривой получаем, обозначив координаты центра тяжести плоской фигуры (пластинки) через 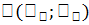, что , . Отсюда

и или ,

.

Пример. Найдем координаты центра тяжести полукруга

, (рисунок 15).

Решение: Очевидно (ввиду симметрии фигуры относительно оси ), что Площадь полукруга равна . Находим :

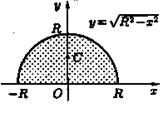
Рисунок 15

Стало быть, . Итак, центр тяжести имеет координаты .

Заключение

Рассмотренные выше примеры практических задач, дают нам ясное представление значимости определенного интеграла для их разрешимости.

Трудно назвать научную область, в которой бы не применялись методы интегрального исчисления, в общем, и свойства определенного интеграла, в частности. Так в процессе выполнения реферата мною были рассмотрены примеры практических задач в области физики, геометрии, механики. Конечно, это еще далеко не исчерпывающий список наук, которые используют интегральный метод для поиска устанавливаемой величины при решении конкретной задачи, и установлении теоретических фактов.

Также определенный интеграл используется для изучения собственно самой математики. Например, при решении дифференциальных уравнений, которые в свою очередь вносят свой незаменимый вклад в решение задач практического содержания. Можно сказать, что определенный интеграл – это некоторый фундамент для изучения математики. Отсюда и важность знания методов их решения.

Из всего выше сказанного понятно, почему знакомство с определенным интегралом происходит еще в рамках средней общеобразовательной школы, где ученики изучают не только понятие интеграла и его свойства, но и некоторые его приложения.

Список использованных источников

1. Дифференциальное и интегральное исчисления для вузов, Том 2 / Н.С. Пискунов – М.: Наука, 1985. -560с.

2. Конспект лекций по высшей математике / Д.Т. Письменный – M.: Айрис – пресс, 2003. – 288 c.

3. Математический анализ для школьников / Л.Н. Понтрягин – 2-е изд., перераб. - М.: Наука, 1983г.

4. Высшая математика – М.: Просвещение, 1993. – 319. Баврин И.И.

5. Высшая математика - М: Наука, 2003 – 684c. Шипачёв В.С.