
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Геометрические приложения определенного интеграла
|
|
РЕФЕРАТ
Тема: Геометрические и физические приложения определенного интеграла
Выполнил:
студент 2 курса
группы ИФ-14 ФЕНМит
Бояркин Сергей
Проверил:
Беломестнова Вера Ревокатовна
Чита 2016
Геометрические приложения определенного интеграла
· Схемы применения определенного интеграла
Пусть требуется найти значение какой – либо геометрической или физической величины  (площадь фигуры, объем тела, давление жидкости на вертикальную пластину и т.д.), связанной с отрезком
(площадь фигуры, объем тела, давление жидкости на вертикальную пластину и т.д.), связанной с отрезком  изменения независимой переменной x. Предполагается, что при разбиении отрезка
изменения независимой переменной x. Предполагается, что при разбиении отрезка  точкой
точкой  на части [a,c] и [c,b] значение величины
на части [a,c] и [c,b] значение величины  , соответствующее всему отрезку
, соответствующее всему отрезку  равно сумме ее значений, соответствующих [a,c] и [c b]
равно сумме ее значений, соответствующих [a,c] и [c b] 
Для нахождения этой величины  можно руководствоваться одной из двух схем: I схема (или метод интегральных сумм) и II схема (или метод дифференциала).
можно руководствоваться одной из двух схем: I схема (или метод интегральных сумм) и II схема (или метод дифференциала).
Первая схема базируется на определении определенного интеграла.
1. Точками  разбить отрезок
разбить отрезок  на
на  частей. В соответствии с этим, интересующая нас величина
частей. В соответствии с этим, интересующая нас величина  разобьется на
разобьется на  «элементарных слагаемых»
«элементарных слагаемых» 
2. Представить каждое «элементарное слагаемое» в виде произведения некоторой функции (определяемой из условия задачи), вычисленной в произвольной точке соответствующего отрезка на его длину:
 .
.
При нахождении приближенного значения  допустимы некоторые упрощения: дугу на малом участке можно заменить хордой, стягивающей ее концы; переменную скорость на малом участке можно приближенно считать постоянной и т. д.
допустимы некоторые упрощения: дугу на малом участке можно заменить хордой, стягивающей ее концы; переменную скорость на малом участке можно приближенно считать постоянной и т. д.
Получим приближенное значение величины  в виде интегральной суммы:
в виде интегральной суммы:

3. Искомая величина  равна пределу интегральной суммы, т. е.
равна пределу интегральной суммы, т. е.

Указанный «метод сумм» основан на представлении интеграла как сумма бесконечно большого числа бесконечно малых слагаемых.
Схема I была применена для выяснения геометрического и физического смысла определенного интеграла.
Вторая схема представляет собой несколько видоизмененную схему I и называется «метод дифференциала» или «метод отбрасывания бесконечно малых высших порядков»:
1) на отрезке  а,b
а,b  выбираем произвольное значение х и рассматриваем переменный отрезок [a,x
выбираем произвольное значение х и рассматриваем переменный отрезок [a,x  На этом отрезке величина
На этом отрезке величина  становится функцией
становится функцией 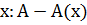 , т. е. считаем, что часть искомой величины
, т. е. считаем, что часть искомой величины  есть неизвестная функция
есть неизвестная функция  , где
, где 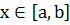 - один из параметров величины
- один из параметров величины  ;
;
2) находим главную часть приращения  при изменении x на малую величину
при изменении x на малую величину  , т. е. находим дифференциал d
, т. е. находим дифференциал d  функции
функции  , где
, где  определяемая из условия задачи, функция переменной x (здесь также возможны различные упрощения);
определяемая из условия задачи, функция переменной x (здесь также возможны различные упрощения);
3) считая, что  при
при 

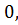 находим искомую величину путем интегрирования
находим искомую величину путем интегрирования  в пределах от
в пределах от  до
до  :
:

· Вычисление длины дуги плоской кривой
Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой,  , где
, где  .
.
Под длиной дуги AB понимается предел, к которому стремиться длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремиться к нулю.
Покажем, что если функция  и ее производная
и ее производная  непрерывна на отрезке
непрерывна на отрезке  , то кривая АВ имеет длину, равную
, то кривая АВ имеет длину, равную
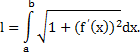
Применим схему I (метод сумм).
1. Точками  разобьем отрезок
разобьем отрезок 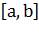 на
на  частей (рис. 2). Пусть этим точкам соответствуют точки
частей (рис. 2). Пусть этим точкам соответствуют точки  на кривой AB. Проведем хорды
на кривой AB. Проведем хорды 
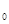



 , длины которых обозначим соответственно через
, длины которых обозначим соответственно через 
|

Получим ломанную  длина которой равна
длина которой равна

2. Длину хорды (или звена ломаной)  можно найти по теореме Пифагора из треугольника с катетами Δ
можно найти по теореме Пифагора из треугольника с катетами Δ  и Δ
и Δ  :
:
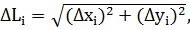 где
где  ,
, 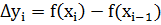 .
.
По теореме Лагранжа о конечном приращении функции
 поэтому
поэтому
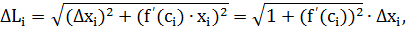
а длина всей ломанной  равна
равна

3. Длина 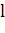 кривой AB, по определению, равна
кривой AB, по определению, равна

Заметим, что при 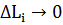 также и
также и  и, следовательно,
и, следовательно,  . Функция
. Функция  непрерывна на отрезке
непрерывна на отрезке  так как, по условию, непрерывна функция
так как, по условию, непрерывна функция 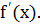 Следовательно, существует предел интегральной суммы (1), когда
Следовательно, существует предел интегральной суммы (1), когда  :
:

Таким образом,

Если уравнение кривой АВ задано в параметрической форме
 ,
,
Где  и
и 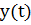 – непрерывные функции с непрерывными производными и
– непрерывные функции с непрерывными производными и  ,
,  , то длина
, то длина  кривой АВ находится по формуле
кривой АВ находится по формуле

Формула (3) может быть получена из формулы (2) подстановкой
 ,
, 

· Вычисление объема тела
Вычисление объема тела по известным площадям параллельных сечений.
Пусть требуется найти объем  тела, причем известны площади
тела, причем известны площади  сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси
сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси 
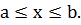
Применим схему II (метод дифференциала).

1. Через произвольную точку 

 проведем плоскость, перпендикулярную оси
проведем плоскость, перпендикулярную оси 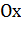 (рис. 3). Обозначим через
(рис. 3). Обозначим через  площадь сечения тела этой плоскостью;
площадь сечения тела этой плоскостью;  считаем известной и непрерывно изменяющейся при изменении
считаем известной и непрерывно изменяющейся при изменении  . Через
. Через 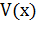 обозначим объем части тела, лежащее левее плоскости. Будем считать, что на отрезке
обозначим объем части тела, лежащее левее плоскости. Будем считать, что на отрезке  величина
величина  есть функция от x, т. е.
есть функция от x, т. е.
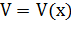

2. Находим дифференциал  функции
функции  Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось
Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось 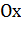 в точках
в точках  , который приближенно может быть принят за цилиндр с основанием
, который приближенно может быть принят за цилиндр с основанием  и высотой
и высотой  . Поэтому дифференциал объема
. Поэтому дифференциал объема  .
.
3. Находим искомую величину  путем интегрирования
путем интегрирования  в пределах от
в пределах от 


 .
.
Полученная формула называется формулой объема тела  по площади параллельных сечений.
по площади параллельных сечений.
Объем тела вращения.
Пусть вокруг оси  вращается криволинейная трапеция, ограниченная непрерывной линией
вращается криволинейная трапеция, ограниченная непрерывной линией  , отрезком
, отрезком  и прямыми
и прямыми  и
и  (рис. 4). Полученная от вращения фигура называется телом вращения.
(рис. 4). Полученная от вращения фигура называется телом вращения.

Сечение этого тела плоскостью, перпендикулярной оси  , проведенной через произвольную точку
, проведенной через произвольную точку  оси
оси 
 , есть круг с радиусом
, есть круг с радиусом  . Следовательно,
. Следовательно,

Применяя формулу (4) объема тела по площади параллельных сечений, получаем
|
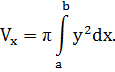
Если криволинейная трапеция ограничена графиком непрерывной функции  и прямыми
и прямыми  , то объем тела, образованного вращением этой трапеции вокруг оси
, то объем тела, образованного вращением этой трапеции вокруг оси  , по аналогии с формулой (5), равен
, по аналогии с формулой (5), равен
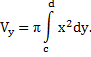
· Вычисление площади поверхности вращения
Пусть кривая АВ является графиком функции  , где
, где 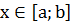 , а функция
, а функция  и ее производная
и ее производная  непрерывны на этом отрезке.
непрерывны на этом отрезке.
Найдем площадь  поверхности, образованной вращением кривой АВ вокруг оси
поверхности, образованной вращением кривой АВ вокруг оси  .
.
Применим схему II (метод дифференциала).
1. Через произвольную точку  проведем плоскость, перпендикулярную оси
проведем плоскость, перпендикулярную оси 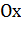 . Плоскость пересекает поверхность вращения по окружности с радиусом
. Плоскость пересекает поверхность вращения по окружности с радиусом  (рис. 5). Величина
(рис. 5). Величина 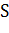 поверхности части фигуры вращения, лежащей левее плоскости, является функцией от
поверхности части фигуры вращения, лежащей левее плоскости, является функцией от  , т.е.
, т.е.

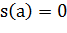 и
и 

2. Дадим аргументу  приращение
приращение 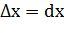 . Через точку
. Через точку  также проведем плоскость, перпендикулярную оси
также проведем плоскость, перпендикулярную оси 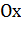 . Функция
. Функция  получит приращение
получит приращение  . Найдем дифференциал площади
. Найдем дифференциал площади  , заменяя образованную между сечениями фигуру усеченным конусом, образующая которого равна
, заменяя образованную между сечениями фигуру усеченным конусом, образующая которого равна  , а радиусы оснований равны
, а радиусы оснований равны 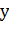 и
и  . Площадь его боковой поверхности равна
. Площадь его боковой поверхности равна

Отбрасывая произведение  как бесконечно малую высшего порядка, чем
как бесконечно малую высшего порядка, чем  получаем
получаем 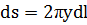 , или, так как
, или, так как
 , то
, то 
3. Интегрируя полученное равенство в пределах 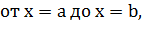 получаем
получаем
 .
.
Если кривая AB задана параметрическими уравнениями 






 то формула для площади поверхности вращения принимает вид
то формула для площади поверхности вращения принимает вид
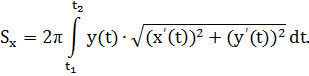
· Вычисление площади плоской фигуры
Пусть функция  непрерывна на сегменте
непрерывна на сегменте  Если
Если  на [a,b], то площадь S криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=a, x=b, равна интегралу
на [a,b], то площадь S криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=a, x=b, равна интегралу

Если же  на
на  то —
то —  на
на 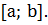 Поэтому площадь S соответствующей криволинейной трапеции выразится формулой
Поэтому площадь S соответствующей криволинейной трапеции выразится формулой

Если, наконец, кривая  пересекает ось Ох, то сегмент
пересекает ось Ох, то сегмент  надо разбить на части, в пределах которых
надо разбить на части, в пределах которых  не меняет знака, и к каждой такой части применить ту из формул, которая ей соответствует.
не меняет знака, и к каждой такой части применить ту из формул, которая ей соответствует.
· Вычисление площади цилиндрической поверхности

Введем дугу  в качестве параметра; тогда не только уравнения
в качестве параметра; тогда не только уравнения  и
и  кривой AB заменятся уравнениями
кривой AB заменятся уравнениями  и
и  но и уравнение
но и уравнение  перейдет в уравнение
перейдет в уравнение  . Впишем в кривую АВ ломаную
. Впишем в кривую АВ ломаную 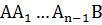 и, в соответствии с этим, в кривую CD – ломаную
и, в соответствии с этим, в кривую CD – ломаную  , из трапеций
, из трапеций  составим призматическую поверхность, вписанную в рассматриваемую цилиндрическую поверхность. Под площадью цилиндрической поверхности будем понимать предел P площади Q призматической поверхности при стремлении к нулю наибольшей из частичных дуг. Полагая, что
составим призматическую поверхность, вписанную в рассматриваемую цилиндрическую поверхность. Под площадью цилиндрической поверхности будем понимать предел P площади Q призматической поверхности при стремлении к нулю наибольшей из частичных дуг. Полагая, что  , имеем
, имеем

Предел суммы будет вычисляться по формуле

в которой легко узнать интегральную сумму. Окончательно
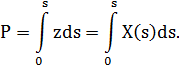
Возвращаясь к произвольному параметру t, легко получить и общую формулу

Наконец, для случая явного задания кривой АВ: y=f(x)  эта формула перепишется так:
эта формула перепишется так:

определенный интеграл геометрический физический
Date: 2016-05-23; view: 3542; Нарушение авторских прав