Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Входные и выходные данные алгоритма
|
|
Входные данные: трёхдиагональная матрица A (элементы 
), вектор B (элементы 
).
Выходные данные: вектор x (элементы 
).
Объём выходных данных: n.
Входные данные: трёхдиагональная матрица A (элементы 
), вектор B (элементы 
).
Выходные данные: матрица y (элементы 
).
Объём выходных данных: N1 * N2.
Свойства алгоритма
Продольно-поперечная схема является одной из первых экономичных схем. Она сочетает в себе лучшее качество явной схемы - экономичность и неявной - устойчивость. Основной идеей экономичных разностных схем является сведение многомерной задачи к цепочке одномерных задач.
При переходе от слоя j к слою j +1 требуется O(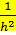
) арифметических действий. Чтобы найти 
при 
по начальным данным требуется, очевидно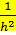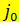, O() 
= O(
) операций, то есть число операций пропорционально числу используемых узлов пространственно-временной сетки 
.
Продольно-поперечная схема равномерно и безусловно устойчива по начальным данным, так как при переходе с одного целого слоя на следующий целый слой ошибки начальных данных не нарастают.
При переходе с целого слоя на целый погрешность локальной аппроксимации на равномерных сетках есть 
, т.е. продольно-поперечная схема имеет второй порядок аппроксимации по всем переменным.
-
Date: 2016-05-23; view: 752; Нарушение авторских прав