Математическое описание алгоритма

Рассмотрим в области

(1.1)

двумерное нелинейное уравнение теплопроводности

(1.2)

с начальными

,

(1.3)

и граничными условиями

.

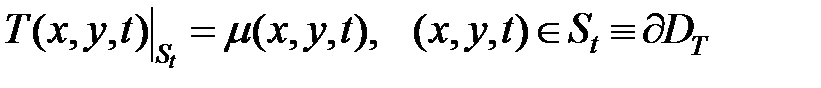(1.4)

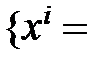
Введем в области сетку узлов , , , , , , а на отрезке 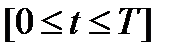сетку узлов .

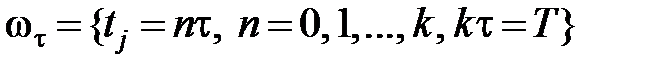Запишем разностную схему для заданной задачи:

(1.5)

где

,

(1.6)

.

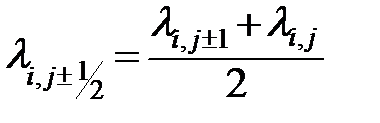(1.7)

Зафиксировав в первом из уравнений системы j, получим систему уравнений относительно значений , где , состоящую из линейного уравнения, которую можно решить методом прогонки.

В целом систему (1.5) на каждом половинном временном слое можно представить как независимую задачу (для каждого фиксированного j), решаемую методом прогонки.

Аналогично решение второго из уравнений системы (1.5) на каждом слое представляет собой решение 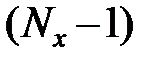независимой задачи при фиксированном i. Каждая из указанных задач является системой линейных уравнений относительно значений сеточной функции по неявному направлению и решается методом прогонки.

Сеточная функция 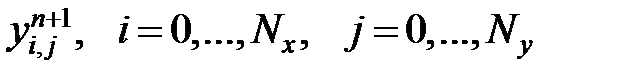является приближенным решением задачи (1.1)–(1.3).

По каждому из неявных направлений разностная схема является линейной и может быть записана в следующем виде:

,

(1.8)

,

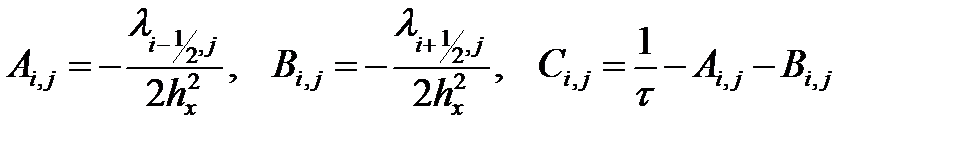(1.9)

(1.10)

и соответственно

,

(1.11)

,

(1.12)

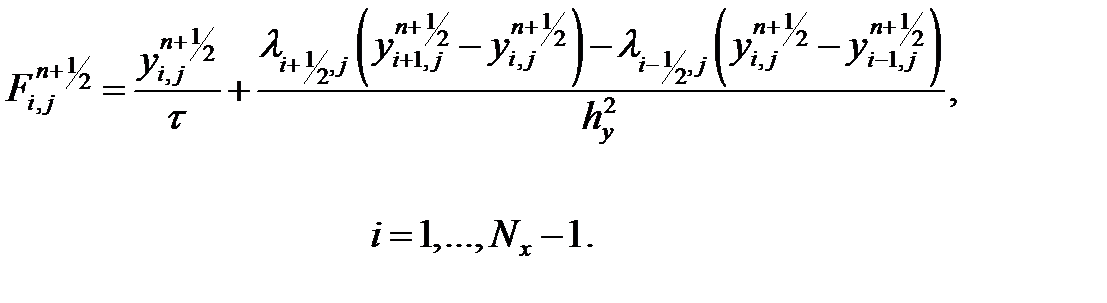
(1.13)

Для решения уравнений (1.8) и (1.11) воспользуемся формулами прогонки

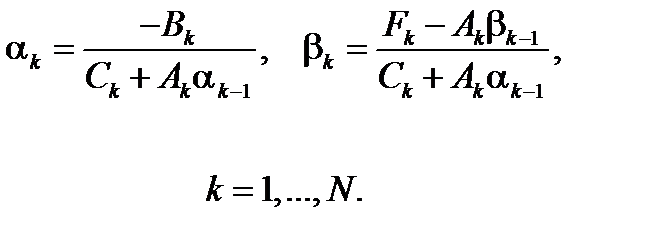
(1.14)

где – индекс неявного направления.

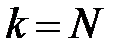Из граничных условий при и определяются значения прогоночных коэффициентов. При этом и равны нулю, а значения и определяются из соответствующих краевых условий.

Date: 2016-05-23; view: 814; Нарушение авторских прав