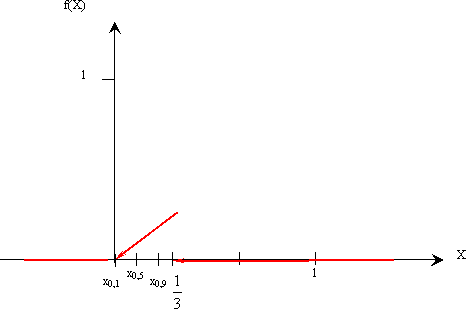
В) квантили порядка 0,1; 0,5; 0,9 и показать их на графике

РЕШЕНИЕ

1) Найдем плотность распределения случайной величины Х.

f(Х) = F '(x)

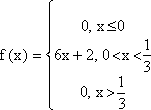
2) Определим математическое ожидание случайной величины Х:

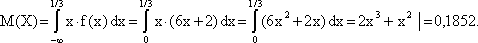
3) Определим дисперсию случайной величины Х:

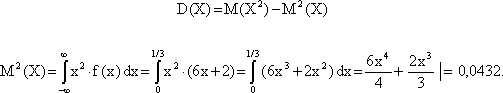
4) Вычислим среднеквадратичное отклонение величины Х от среднего:

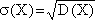
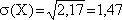
5) Найдем медиану:

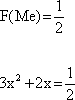
Решим квадратное уравнение: D = 4 + 6 = 10, x1 = 0,193; x2 = -0,86.

Таким образом, Me = 0,193.

7) Для определения моды построим график плотности распределения:

Построим график функции распределения:

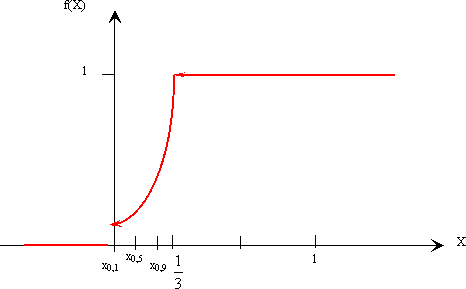
Из графика видно, что случайная величина не имеет моды.

7) Найдем вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу (1/6; 1/3).

P (x1 < X < x2) = F(x1) – F(x2)

P (1/6 < X < 1/3) = F(1/3) – F(1/6) =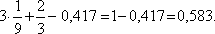

8) Найдем квантили:

- порядка 0,1

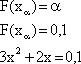
После решения квадратного уравнения получаем: x1 = 0,047, x2 = -0,71.

X0,1 = 0,047.

- порядка 0,5

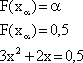
После решения квадратного уравнения получаем: x1 = 0,193; x2 = -0,86.

X0,5 = 0,193.

- порядка 0,9

После решения квадратного уравнения получаем: x1 = 0,31; x2 = -0,98.

X0,9 = 0,31

Изобразим квантили на графиках (см. графики выше).

ЗАДАЧА № 17

Диаметр детали, изготовленной заводом, является случайной величиной, распределенной по нормальному закону. Дисперсия ее равна 0,0001, а математическое ожидание – 2,5 см. Найти границы, в которых с вероятностью 0,9973 заключен диаметр наудачу взятой детали.

РЕШЕНИЕ

I Способ

Для решения используем формулу отклонения случайной величины, распределенной по нормальному закону, от среднего значения:

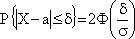
Вероятность попадания случайной величина в заданный интервал нам известна по условию Р = 0,9973,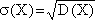

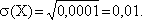
Подставим вместо Р имеющееся значение вероятности:

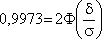
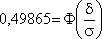
По таблице находим аргумент 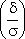= 3, тогда? = 0,03.

Значит, искомые границы следующие: 2,47? X? 2,53.

Покажем этот интервал на рисунке:

II Способ

Вероятность попадания случайной величины в заданный интервал, равная 0,9973 соответствует трехсигмовому интервалу отклонения случайной величины от среднего. То есть, если 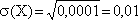то тогда отклонение в обе стороны от математического ожидания (среднего) составит (0,01? 3) 0,03.

Значит, искомые границы следующие: 2,47? X? 2,53.

ОТВЕТ: Диаметр наудачу взятой детали с вероятностью 0,9973 заключен в следующие границы: 2,47? X? 2,53.

ЗАДАЧА № 18

Число аварий на угольных шахтах подчиняется закону гамма-распределения с параметрами? = 0,429,? = 1,68 • 10-3. Определить вероятность того, что число аварий будет находится в пределах х1 = 500 и х2 = 600.

РЕШЕНИЕ

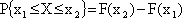
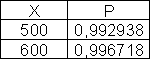
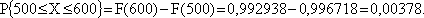
ОТВЕТ: Вероятность того, что число аварий будет находится в пределах х1 = 500 и х2 = 600, равна 0,00378.

ЗАДАЧА № 19

Испытываются два независимо работающих элемента. Длительность безотказной работы первого имеет показательное распределение F1(t) = 1 – e-0,05t, второго - F2(t) = 1 – e-0,1t. Найти вероятность того, что за время длительностью 18 часов:

Date: 2016-05-18; view: 3911; Нарушение авторских прав