Вычислить вероятность того, что некоторое событие не произойдет, если известно, что при n испытаниях оно в среднем происходит в m случаях

ЗАДАЧА № 2

Расписание одного дня содержит 5 уроков. Определить количество таких расписаний при выборе из 11 дисциплин.

РЕШЕНИЕ

Количество различных расписаний можно определить с помощью формулы комбинаторики для размещения по 5 из 11 элементов. Выбор размещения определяется тем, что при построении расписания необходимо учитывать порядок следования уроков.

ОТВЕТ: При данных условиях можно составить 55440 различных расписаний.

ЗАДАЧА № 3

Сколькими способами можно выбрать 3 дежурных из группы в 20 человек?

РЕШЕНИЕ

Так как для данной задачи несущественен порядок выбора, то воспользуемся формулой комбинаторики для сочетания из 20 по 3:

ОТВЕТ: Трех дежурных из группы в 20 человек можно выбрать 1140 способами.

Задача №4

Вычислить вероятность того, что некоторое событие не произойдет, если известно, что при n испытаниях оно в среднем происходит в m случаях.

РЕШЕНИЕ

1) Обозначим событие А = «Событие произошло». Определим вероятность появления данного события. Для этого воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:

где m – число исходов, при которых появляется событие А,

n – общее число элементарных несовместных равновозможных исходов.

2) Определим вероятность того, что событие А не произойдет, по формуле:

ОТВЕТ: Вероятность того, что событие не произойдет, равна

ЗАДАЧА №5

Из 60 вопросов, входящих в экзаменационные билеты, студент подготовил 50. Какова вероятность того, что взятый наудачу студентом билет, содержащий 2 вопроса, будет состоять из подготовленных им вопросов?

РЕШЕНИЕ

1) Обозначим событие А = «Вытянутый студентом билет состоит из подготовленных им билетов». Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:

где m – число исходов, при которых появляется событие А,

n – общее число элементарных несовместных равновозможных исходов.

2) Определим n. Общее число билетов определяется сочетанием по 2 из 60:

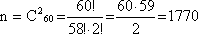
3) Количество билетов, вопросы которых студент знает, определяется сочетанием по 2 из 50:

4) Определим вероятность события А:

ОТВЕТ: Вероятность того, что взятый наудачу студентом билет, содержащий 2 вопроса, будет состоять из подготовленных им вопросов равна Р(А) = 0,69. То есть, если будет, например, 100 таких студентов, то 69 из них вытянут билеты, к вопросам которых они подготовлены.

ЗАДАЧА № 6

Какова вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти?

РЕШЕНИЕ

1) Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:

где m – число исходов, при которых появляется событие А,

n – общее число элементарных несовместных равновозможных исходов.

2) Определим n. Для этого воспользуемся формулой сочетания по 4 из 52(так как нас не интересует порядок вытянутых карт):

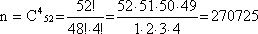
3) Обозначим событие А = «Из 4 вынутых карт 2 принадлежат пиковой масти». Найдем вероятность вытягивания 2 пиковых карт по формуле сочетания по 2 из 13 (так как всего карт пиковой масти 13):

4) Найдем вероятность вытягивания оставшихся двух карт не пиковой масти по формуле сочетания по 2 из 39 (52-13).

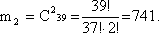
5) Полученные значения мы перемножаем: m = m1? m2

m = 78? 741 = 57798

6) Найдем вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти:

ОТВЕТ: Вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти, равна 0,21.

Задача № 7

Один из мальчиков родился в марте, а другой в апреле. Какова вероятность того, что оба они родились в первой неделе месяца?

РЕШЕНИЕ

1) Вероятность того, что первый мальчик родился в первой неделе марта равна:

2) Вероятность того, что второй мальчик родился в первой неделе апреля равна:

3) Вероятность того, что оба они родились в первой неделе месяца, равна P(A)? P(B):

ОТВЕТ: Вероятность того, что оба мальчика родились в первой неделе месяца равна 0,05.

ЗАДАЧА №8

Для разрушения моста достаточно попадания одной бомбы. Найти вероятность того, что мост будет разрушен, если на него будут сброшены 4 бомбы с вероятностями попадания соответственно 0,3; 0,4; 0,6; 0,7.

РЕШЕНИЕ

Для определения вероятности воспользуемся формулой вероятности появления хотя бы одного из n событий:

Обозначим события: А1 = «Первая бомба попала на мост»

А2 = «Вторая бомба попала на мост»

А3 = «Третья бомба попала на мост»

А4 = «Четвертая бомба попала на мост»

В нашем случае:

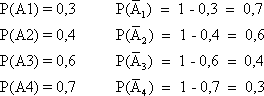
Тогда P (A1 + A2 + A3 + A4) = 1 – 0,7? 0,6? 0,4? 0,3 = 0,9496.

ОТВЕТ: Вероятность того, что мост будет разрушен, если на него будут сброшены 4 бомбы с заданными вероятностями попадания, равна 0,9496, то есть это достаточно достоверное событие.

ЗАДАЧА № 9

Чему равна вероятность того, что при одновременном бросании трех игральных костей 2 очка появятся на 2 костях?

РЕШЕНИЕ

Обозначим события: А = «2 очка выпали на первой кости»

В = «2 очка выпали на второй кости»

С = «2 очка выпали на третьей кости»

Искомое событие X описывается следующей комбинацией:

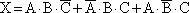
Так как события А, В и С несовместные и независимые, то вероятность события Х определяется по формуле:

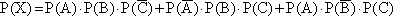
P(X) = 0,17? 0,17? 0,83 + 0,83? 0,17? 0,17 + 0,17? 0,83? 0,17 = 0,17? 0,17? 0,83? 3 = 0,07.

ОТВЕТ: Вероятность того, что при одновременном бросании трех игральных костей 2 очка появятся на 2 костях, равна 0,07.

ЗАДАЧА № 10

Некоторое изделие может поступить для обработки в случайном порядке на один из трех станков с вероятностями соответственно равными Р1 = 0,2; Р2 = 0,3; Р3 = 0,5. При обработке на первом станке вероятность брака равна 0,02, на втором – 0,03, на третьем – 0,05. Найти вероятность того, что поступившее в цех изделие после обработки окажется удовлетворяющим техническим условиям.

РЕШЕНИЕ

Обозначим события: А = «Изделие удовлетворяет техническим условиям»

В1 = «Изделие обрабатывалось на первом станке»

В2 = «Изделие обрабатывалось на втором станке»

В3 = «Изделие обрабатывалось на третьем станке»

Для решения поставленной задачи используем формулу полной вероятности:

ОТВЕТ: Вероятность того, что поступившее в цех изделие после обработки окажется удовлетворяющим техническим условиям, равна 0,745.

ЗАДАЧА №11

Пусть в условиях предыдущей задачи поступившее в цех изделие после обработки оказалось удовлетворяющим техническим условиям. Какова вероятность того, что изделие обрабатывалось на третьем станке?

РЕШЕНИЕ

Для решения данной задачи применим формулу Бейеса:

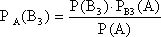
ОТВЕТ: Вероятность того, что изделие обрабатывалось на третьем станке, при том что оно оказалось удовлетворяющим техническим условиям, равна 0,638.

ЗАДАЧА № 12

Вероятность изготовления на автоматическом станке стандартной детали равна 0,9. Определить вероятность того, что из трех наудачу взятых деталей: а) две окажутся стандартными; б) все три окажутся стандартными.

РЕШЕНИЕ

Для решения используем формулу Бернулли:

а) p = 0,9; q = 1 – 0,9 = 0,1

б) p = 0,9; q = 1 – 0,9 = 0,1

ОТВЕТ: Вероятность того, что из трех наудачу взятых деталей две окажутся стандартными, равна 0,243; а того, что все три окажутся стандартными, - 0,729.

ЗАДАЧА №13

Вероятность выхода из строя за некоторое время Т одного конденсатора равна 0,1. Найти вероятность того, что из 100 конденсаторов в течение времени Т из строя выйдут: а) ровно 16 конденсаторов; б) от 4 до 19 конденсаторов.

РЕШЕНИЕ

а) Для решения используем формулу Бернулли:

k = 16, n = 100, p = 0,1; q = 1 – 0,1 = 0,9

б) Для решения используем интегральную теорему Муавра-Лапласа:

По таблице(Приложение 2) определим значение функции при данных значениях х:

Ф(-2) = -Ф(2) = 0,4772; Ф(3) = 0,49865

ОТВЕТ: Вероятность того, что из 100 конденсаторов в течение времени T из строя выйдут ровно 16 конденсаторов, равна 0,019, а от 4 до 19 конденсаторов – 0,02145.

ЗАДАЧА № 14

Игральная кость брошена два раза. Составить закон распределения случайной величины Х – числа появления двойки. Найти математическое ожидание и дисперсию случайной величины.

РЕШЕНИЕ

1) Составим закон распределения случайной величины Х:

X 0 1 2

P P1 P2 P3

2) Найдем вероятность события А = «При бросании кости выпала двойка». Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:

где m – число исходов, при которых появляется событие А, n – общее число элементарных несовместных равновозможных исходов.

В нашем случае m = 1, а n = 6 (так как на кости шесть граней с числами).

Тогда

3)Для определения вероятностей того, что двойка выпадет 0, 1 или 2 раза воспользуемся формулой Бернулли:

4) Найдем вероятность того, что двойка на игральной кости не выпадет ни разу (Х=0).

5) Найдем вероятность того, что двойка на игральной кости выпадет один раз (Х=1).

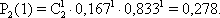
6) Найдем вероятность того, что двойка на игральной кости выпадет два раза (Х=2).

7) Заполним теперь таблицу, выражающую закон распределения случайной величины Х:

X 0 1 2

P 0,694 0,278 0,028

8) Определим математическое ожидание данной случайной величины Х (математическое ожидание характеризует среднее значение случайной величины при большом числе испытаний):

М(Х) = 0? 0,694 + 1? 0,278 + 2? 0,028 = 0,334.

9) Определим дисперсию для данной случайной величины по формуле (дисперсия характеризует средний квадрат отклонения случайной величины от среднего):

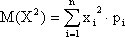
10) Определим среднеквадратическое отклонение, которое характеризует среднее отклонение случайной величины от среднего, по формуле:

ОТВЕТ: Математическое ожидание случайной величины равно М(Х) = 0,334. Дисперсия случайной величины равна Д(Х) = 0,278.

ЗАДАЧА № 15

Дискретная случайная величина Х задана законом распределения:

X 2 5 8

P 0,4 P2 0,1

Найти: Р2; функцию распределения F(х) и построить ее график; математическое ожидание; дисперсию и среднеквадратическое отклонение случайной величины Х. Найти закон распределения случайной величины Y, где Y = 2X, Y = X2.

РЕШЕНИЕ

1) Определим Р2. Так как сумма всех вероятностей, указанных в таблице, должна быть равна единице (то есть Р1 + Р2 + Р3 = 1), то Р2 найдем из формулы:

Р2 = 1 - Р1 - Р3

Р2 = 1 – 0,4 – 0,1 = 0,5.

2) Построим функцию распределения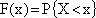

а) Рассмотрим первый интервал х <= 2: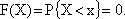

б) Рассмотрим второй интервал 2 < х <= 5: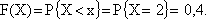

в) Рассмотрим третий интервал 5 < х <= 8: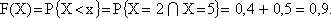

г) Рассмотрим четвертый интервал х > 8:

Запишем закон распределения:

3) Построим график функции распределения:

4) Определим математическое ожидание данной случайной величины Х (математическое ожидание характеризует среднее значение случайной величины при большом числе испытаний):

М(Х) = 2? 0,4 + 5? 0,5 + 8? 0,1 = 4,1.

5) Определим дисперсию для данной случайной величины по формуле (дисперсия характеризует средний квадрат отклонения случайной величины от среднего):

Д(Х) = М(Х2) – М2(Х)

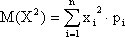
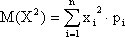
М(Х2) = 22? 0,4 + 52? 0,5 + 82? 0,1 = 20,5.

Д(Х) = 20,5 – 4,12 = 3,69.

6) Определим среднеквадратическое отклонение, которое характеризует среднее отклонение случайной величины от среднего, по формуле:

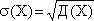
7) Составим закон распределения для функций Y = 2X и Y = X2

X 2 5 8

Y=2X 4 10 16

Y= 4 25 64

P 0,4 P2 0,1

ЗАДАЧА №16

Случайная величина Х задана функцией распределения F(x):

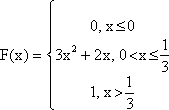
Найти: а) плотность распределения вероятностей, математическое ожидание, дисперсию, СКО, медиану и моду случайной величины Х;

б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу (1/6; 1/3);