Средняя квадратическая величина

В ранжированном ряду средняя квадратическая величина рассчитывается по невзвешенной (простой) форме:

где

х – варианты ранжированного ряда; n – общее число вариант.

Взвешанная форма средней квадратической величины, которая используется для дискретного или интервального ряда, выражается следующим образом:

Средняя квадратическая величина, как самостоятельный вид средних, имеет ограниченное применение.

Средняя геометрическая величина имеет простую (невзвешенную) и взвешенную формы.

Средняя геометрическая простая величина, рассчитываемая в ранжированном ряду, выражается следующим образом:

где П – знак произведения; х – варианты; n – общее число вариант в ранжированном ряду.

Для дискретного или интервального ряда средняя геометрическая рассчитывается по взвешенной форме:

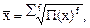
где f – частота дискретного или интервального ряда.

Средняя геометрическая величина применяется в тех случаях, когда варианты связаны между собой знаком произведения, т.е. главным образом при расчёте относительных показателей динамики: коэффициентов (темпов) роста, прироста и др.

Если имеет место дискретный или интервальный ряд, то при расчёте средней целесообразно воспользоваться взвешенной формой средней геометрической величины.

Средняя гармоническая величина. Название средней гармонической величины неслучайно, так эта средняя "гармонирует" со средней арифметической величиной.

Для ранжированного ряда используется средняя гармоническая простая величина, которую можно записать следующим образом.

где n – общая численность вариант;

- обратное значение варианты.

В дискретный или интервальных рядах используются средняя гармоническая взвешенная величина:

где W – произведение варианты на частоту (взвешенная варианта, xf).

Средняя гармоническая величина применяется главным образом в тех случаях, когда варианты ряда представлены обратными значениями, а частоты (веса) скрыты в общем объеме изучаемого признака.

Date: 2016-05-18; view: 420; Нарушение авторских прав