
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Цифровые и микропроцессорные устройства 2 page
|
|
Пример 4.  = – 0,1101;
= – 0,1101; 
Из формулы (4) и примеров видно, что изображение положительных чисел в дополнительном коде совпадает с изображением их в прямом коде. Для представления отрицательного двоичного числа в дополнительном коде необходимо в знаковом разряде поставить единицу, произвести замену цифр исходного числа на обратные и к полученному коду прибавить единицу младшего разряда.
Обратное преобразование, т.е. получение числа из дополнительного кода выполняется по тому же правилу, что и получение дополнительного кода.
Пример 5. 
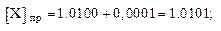
X = – 0,0101.
Дополнительный код получил более широкое применение, так как обеспечивает более высокое быстродействие.
Обратный код отрицательного двоичного числа находится как дополнения модуля до двух без единицы младшего разряда. Обратный код для двоичных чисел, меньших единицы, образуется по формуле:
 (5)
(5)
Пример 6. 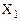 = + 0,1101;
= + 0,1101; 
Пример 7.  = – 0,1101;
= – 0,1101;
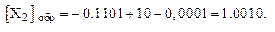
Из формулы и примеров видно, что изображение положительного числа в обратном коде совпадает с его изображением в прямом коде. Обратный код отрицательного числа образуется заменой цифр исходного числа на обратные и постановкой единицы в знаковый разряд.
Переход от обратного кода к прямому осуществляется по тому же правилу, что и от прямого к обратному.
Пример 8. 
 X = – 0,0100.
X = – 0,0100.
Арифметические операции над двоичными числами с фиксированной точкой
Основной операцией, которая используется в цифровых устройствах при различных вычислениях, является операция алгебраического сложения (сложение положительных и отрицательных чисел). Вычитание, умножение и деление также выполняются с помощью операции сложения и некоторых других действий.
Сложение чисел в цифровых устройствах производится так же, как и при ручном счете, т.е. путем поразрядного суммирования чисел, начиная с младших разрядов. Сложение двоичных чисел выполняется в соответствии с таблицей:
| 0 + 0 = 0; | 0 + 1 = 1; | 1 + 0 = 1; | 1 + 1 = 10. |
Пример 1. Выполним сложение двух положительных двоичных чисел, представленных в естественной форме:

Из примера следует, что начиная со второго разряда сложение производится с учетом переноса из соседнего младшего разряда.
Вычитание двоичных чисел выполняется в соответствии с таблицей:
| 0 – 0 = 0; | 1 – 0 = 1; | 1 – 1 = 0; | 10 – 1 = 1. |
Пример 2. Выполним вычитание, т.е. сложение двух двоичных чисел с разными знаками, представленных в естественной форме:

Так как | 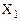 | > |
| > |  |, то выполняется вычитание
|, то выполняется вычитание  из
из 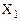 и результату присваивается знак плюс.
и результату присваивается знак плюс.
Из примера следует, что при вычитании происходит заем из соседнего старшего разряда. Следовательно, при сложении и вычитании двоичных чисел в естественной форме используются различные правила, поэтому вычитание заменяется сложением в машинных кодах.
При алгебраическом сложении двоичных чисел в обратном и дополнительном кодах используются следующие правила:
а) знаковые разряды суммируются так же, как и значащие разряды числа;
б) единица переноса из знакового разряда при сложении в дополнительном коде отбрасывается, а в обратном коде для получения правильного результата эта единица прибавляется к младшему разряду суммы, компенсируя величину  . Такой перенос называется циклическим;
. Такой перенос называется циклическим;
в) если в знаковом разряде суммы получился нуль, то сумма положительна и для перехода к естественной форме числа обратное преобразование не требуется. Если же в знаковом разряде суммы получилась единица, то сумма отрицательна и требуется обратное преобразование.

Пример 3. Выполним суммирование двоичных чисел 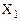 = + 0,11001 и
= + 0,11001 и  = – 0,01011 в обратном коде:
= – 0,01011 в обратном коде:
Результат получился положительным, т.е. 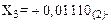
Пример 4. Выполним суммирование тех же двух двоичных чисел 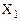 = + 0,11001 и
= + 0,11001 и  = – 0,01011 в дополнительном коде:
= – 0,01011 в дополнительном коде:

Результат получился положительным и совпал с результатами суммирования в обратном коде и вычитания в естественной форме.
Пример 5. Поменяем знаки чисел 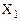 и
и  и выполним суммирование в дополнительном коде. Результат получится отрицательным и потребуется обратное преобразование.
и выполним суммирование в дополнительном коде. Результат получится отрицательным и потребуется обратное преобразование.
 |
При сложении чисел одного знака может произойти переполнение разрядной сетки, что приведет к искажению результата. На практике для выявления переполнения разрядной сетки применяют модифицированные машинные коды, в которых два знаковых разряда. Для положительных чисел в знаковых разрядах записывается 00, для отрицательных – 11. Появление комбинаций 01 или 10 в знаковых разрядах свидетельствует о переполнении разрядной сетки, т. е. является сигналом ошибки. Например, двоичное число X = – 0,1101 в модифицированном дополнительном коде будет записано следующим образом:
 = 11.0011.
= 11.0011.
Пример 6. Выполним суммирование двух десятичных чисел 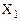 = + 0,450 и
= + 0,450 и  = – 0,575 в двоичной СС с точностью пять знаков после запятой в дополнительном модифицированном коде и сравним результаты суммирования в двоичной и десятичной СС.
= – 0,575 в двоичной СС с точностью пять знаков после запятой в дополнительном модифицированном коде и сравним результаты суммирования в двоичной и десятичной СС.
 |
Так как |
 | > |
| > | 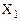 |, то в естественной форме следует выполнить вычитание числа
|, то в естественной форме следует выполнить вычитание числа 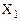 из числа
из числа  и результату присвоить знак минус.
и результату присвоить знак минус.
 |
Результаты суммирования в естественной форме и дополнительном модифицированном коде совпадают.
Умножение двоичных чисел в цифровых устройствах производится по тем же правилам, что умножение десятичных чисел и делится на два этапа.
На первом этапе определяется знак произведения путем суммирования по модулю 2 знаковых разрядов сомножителей. Если знаковые разряды сомножителей одинаковы и равны 0 или 1, то сумма по модулю 2 равна 0 (произведение положительно), если же знаковые разряды сомножителей не совпадают, то эта сумма будет равна 1 (произведение отрицательно).
На втором этапе определяется абсолютное значение произведения путем перемножения этих чисел без учета знака (кодовое умножение). Для этого необходимо вычислить частичные произведения, затем сдвинуть их и сложить между собой.
 |
Пример 1. Умножим целые положительные двоичные числа
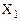 = 1101 и
= 1101 и  = 1011. Умножение выполним, начиная с младшего разряда множителя.
= 1011. Умножение выполним, начиная с младшего разряда множителя.
Суммирование частичных произведений осуществляется в несколько этапов, поскольку арифметическое устройство может выполнять операцию сложения сразу только с двумя числами.
Если умножение выполняется, начиная со старшего разряда множителя, то частичные произведения следует сдвигать вправо.
Особенности арифметических операций над двоичными числами с плавающей точкой
При сложении двоичных чисел с плавающей точкой операции производятся отдельно с мантиссами и порядками. Результат выполнения операции должен представляться в нормализованном виде, поэтому машинная операция сложения чисел с плавающей точкой распадается на четыре этапа:
а) выравниваются порядки слагаемых. Выравнивание порядков производится в сторону большего порядка, с тем чтобы при выравнивании не терять старшие разряды мантиссы. Мантисса преобразуемого числа сдвигается вправо на необходимое количество разрядов;
б) производится преобразование мантисс слагаемых в модифицированный дополнительный или обратный код;
в) мантиссы слагаемых суммируются по правилам сложения дробных чисел с фиксированной точкой;
г) производится нормализация суммы и округление мантиссы в случае необходимости.
Умножение двоичных чисел с плавающей точкой также производится в четыре этапа:
а) определение знака произведения путем сложения по модулю 2 знаковых разрядов мантисс сомножителей;
б) перемножение модулей мантисс по правилам для чисел с фиксированной точкой;
в) определение порядка произведения путем алгебраического сложения порядков сомножителей с использованием дополнительного либо обратного модифицированного кода;
г) нормализация результата и округление мантиссы в случае необходимости.
Сложение двоично-десятичных чисел
Десятичные числа в коде 8421 суммируются по правилам сложения десятичных чисел. Если в тетраде, представляющей десятичный разряд, содержится 10 или более единиц, т.е. возникло переполнение, то формируется единица переноса в старший десятичный разряд, а из суммы вычитается десять единиц. Полученный результат есть цифра соответствующего десятичного разряда суммы. Наличие переполнения тетрады выявляется по наличию переноса в соседнюю старшую тетраду либо по наличию единиц одновременно в разрядах с весовыми коэффициентами 8 и 4 либо 8 и 2 в полученной сумме. В этом случае требуется коррекция суммы. Поскольку в цифровых устройствах вычитание заменяется сложением в дополнительном коде, то вычитание десяти единиц заменяется прибавлением шести единиц, так как число  является дополнительным кодом числа
является дополнительным кодом числа 
Пример 1. Выполним сложение двух десятичных чисел  = 458 и
= 458 и 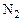 = 629 в десятичной СС и коде 8421 и сравним полученные результаты:
= 629 в десятичной СС и коде 8421 и сравним полученные результаты:
 |
Десятичная система счисления
Код 8421

Результаты сложения в десятичной СС и коде 8421 совпадают. В младшей тетраде коррекция произведена из-за наличия единицы переноса во вторую тетраду. Следует помнить, что коррекция может выполняться в несколько этапов, если в процессе коррекции возникает переполнение.
Символьные коды
Символьные коды устанавливают соответствие букв, знаков препинания, десятичных цифр и других символов двоичным комбинациям. Эти коды можно использовать для хранения и обработки чисел, а также для ввода-вывода информации. Существуют различные символьные коды. Широкое применение получил американский стандартный код обмена информацией ASCII (American Standard Code for Information Interchange). Он является 7-разрядным и позволяет представить  = 128 символов (представляется 96 символов и 32 команды обмена). К каждому символу добавляется один контрольный разряд для контроля символа на четность, т.е. символы передаются и хранятся в памяти в виде 8-разрядных слов.
= 128 символов (представляется 96 символов и 32 команды обмена). К каждому символу добавляется один контрольный разряд для контроля символа на четность, т.е. символы передаются и хранятся в памяти в виде 8-разрядных слов.
Отечественным аналогом кода ASCII является код обмена информацией семиразрядный КОИ-7, который представлен в таблице 2.
Таблица 2 – Символьный код КОИ-7
| Код символа в 16-ричной системе счисления | ||||||
| Младшая цифра | Старшая цифра | |||||
| Пробел | @ | P | Ю | П | ||
| ! | A | Q | А | Я | ||
| « | B | R | Б | Р | ||
| # | C | S | Ц | С | ||
| ¤ | D | T | Д | Т | ||
| % | E | U | Е | У | ||
| & | F | V | Ф | Ж | ||
| ¢ | G | W | Г | В | ||
| ( | H | X | Х | Ь | ||
| ) | I | Y | И | Ы | ||
| A | * | : | J | Z | Й | З |
| B | + | ; | K | [ | К | Ш |
| C | , | < | L | \ | Л | Э |
| D | – | = | M | ] | М | Щ |
| E | . | > | N | Ù | Н | Ч |
| F | / | ? | O | _ | О | Забой |
Например, десятичная цифра 5 представляется кодом  русская буква П –
русская буква П –  знак «+» –
знак «+» – 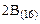 и т. д.
и т. д.
Структурные единицы и форматы цифровых данных
Данными называют информацию, представленную в виде пригодном для ее автоматизированной обработки.
В цифровых устройствах данные представляются в двоично-кодированной форме. Основными структурными единицами данных являются: бит, поле, байт, слово.
Бит (сокращение от англ. binary digit – двоичная цифра) – это такое количество информации, которое может быть записано в одном разряде разрядной сетки, например 0 или 1.
Последовательность битов, имеющая определенный смысл, называется полем (поле кода операции, поле адреса и т.д.).
Поле, состоящее из 8 битов, называется байтом (от англ. byte – слог, часть). Байт в цифровой технике используется для представления и записи любого символа, а также является наименьшей адресуемой единицей для записи и хранения данных в запоминающих устройствах. На основе байтов строятся любые другие укрупненные единицы данных (слово – 2 байта, двойное слово – 4 байта, учетверенное слово – 8 байт, килобайт –  байт, мегабайт –
байт, мегабайт –  байт, гигабайт –
байт, гигабайт – 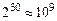 байт, терабайт –
байт, терабайт –  байт).
байт).
Словом называется последовательность, состоящая из строго определенного числа байтов, принятого для данного цифрового устройства.
На основе принятой структуры разнообразные данные организуются в соответствии со следующими форматами:
а) числовые данные с фиксированной точкой делятся на беззнаковые (например, адреса памяти) и обычные числа со знаком. Каждый тип данных может быть представлен в четырех форматах: наименьшем (один байт), коротком (одно слово), среднем (двойное слово), длинном (учетверенное слово);
б) для числовых данных с плавающей точкой используется три формата: короткий (4 байта, из них мантисса со знаком 3 байта, порядок со знаком 1 байт), средний (8 байт, из них мантисса со знаком 53 бит, порядок со знаком 11 бит), длинный (10 байт, из них мантисса со знаком 65 бит, порядок со знаком 15 бит);
в) для представления двоично-десятичных данных применяется два формата: упакованный и неупакованный;
В упакованном формате в каждом байте размещаются две десятичные цифры. Для знака отводится старшая тетрада старшего байта (для положительных чисел – 1100, для отрицательных – 1101). Упакованный формат используется для выполнения арифметических операций.
В неупакованном формате десятичные цифры кодируются в соответствии с американским стандартным кодом обмена информацией ASCII. При этом в каждом байте (в младшей тетраде) размещается только одна десятичная цифра, а в старшей тетраде записывается 0011 (в соответствии с кодом ASCII). Для знака числа отводится старший байт (для положительных чисел –  для отрицательных –
для отрицательных –  ). Неупакованный формат используется для обмена двоично-десятичными данными между процессором и внешними устройствами;
). Неупакованный формат используется для обмена двоично-десятичными данными между процессором и внешними устройствами;
г) для представления и обработки текстовой информации используются специальные информационные структуры переменного формата – строки. Строка представляет непрерывную последовательность битов, байтов, слов или двойных слов. Битовая строка может быть длиной до 1 Гбита, а длина остальных строк может достигать 4 Гбайт.
ЛОГИЧЕСКИЕ ОСНОВЫ ЦИФРОВОЙ ТЕХНИКИ
Понятие о логических функциях, логических элементах и логических устройствах
Одна из причин широкого распространения ЭВМ заключается в том, что они могут решать не только арифметические, но и логические задачи. В противном случае эти машины играли бы только роль быстродействующих арифмометров и не могли бы использоваться для целей управления, поиска лучших вариантов решения и т.п. ЭВМ становятся «думающими» благодаря использованию алгебры логики. Как известно, логика – это наука о законах и формах мышления. Алгебра логики – это начальный раздел математической логики, которая занимается изучением возможностей применения формальных методов для решения логических задач. Иногда алгебру логики называют булевой алгеброй по имени английского математика Д. Буля, который еще в XIX в. разработал основные положения исчисления высказываний. В 40-е гг. XX в. алгебра логики нашла широкое применение при составлении и расчете сложных переключающих схем в автоматических телефонных станциях. Она широко применяется при анализе и синтезе различных цифровых узлов, а также при машинном решении логических задач.
Начальным понятием алгебры логики является понятие высказывания. Под высказыванием понимается любое утверждение, которое может быть истинным или ложным. Над высказыванием можно выполнять некоторые математические операции, так как каждое высказывание можно рассматривать как двоичную переменную. Примером двоичной переменной может служить значение какого-либо разряда двоичного числа, которое может быть нулем либо единицей. В соответствии с двоичной природой высказываний условились называть их логическими переменными и обозначать буквами латинского алфавита, приписывая им значение 1 в случае истинности и значение 0 в случае ложности, например 
 и т.д.
и т.д.
Высказывания могут быть простыми и сложными. Простое высказывание содержит одну простую законченную мысль. Значение истинности простого высказывания не зависит от значений истинности каких-либо других высказываний. Сложным называется высказывание, значение истинности которого зависит от значений других высказываний. Следовательно, любое сложное высказывание можно считать логической (булевой) функцией некоторых двоичных аргументов – простых высказываний, входящих в его состав. Сложные высказывания также могут служить аргументами еще более сложных логических функций, т.е. при построении логических функций справедлив принцип суперпозиции. Отсюда следует, что можно построить логическую функцию любой сложности, пользуясь ограниченным числом логических связок (операций) и принципом суперпозиции.
Термин «логическая операция» означает простейшее действие над логическими аргументами, например логическое отрицание, логическое умножение и т.п.
Если логическая функция содержит только одну логическую операцию, то она называется элементарной.
Электрическая схема, реализующая элементарную логическую функцию называется логическим элементом.
Устройства, реализующие логические функции любой сложности, называются логическими или цифровыми.
Классификация логических устройств
В цифровой технике для обозначения различной информации пользуются кодовыми словами, которые представляют собой последовательность символов 0 и 1 (логических переменных), например: 10111011.
Цифровые устройства (либо их узлы) можно классифицировать по различным признакам.
По способу ввода и вывода кодовых слов различают логические устройства параллельного, последовательного и смешанного действия. В логических устройствах параллельного действия все n символов каждого входного слова подаются одновременно, т.е. в параллельном коде. В такой же форме на выходе образуется выходное слово. Очевидно, что в этом случае в устройстве необходимо иметь отдельный вход (выход) для каждого разряда входного (выходного) слова. В логических устройствах последовательного действия символы входного кодового слова поступают не одновременно, а последовательно во времени, символ за символом, т.е. в последовательном коде. В такой же последовательной форме выдается выходное слово. В логических устройствах смешанного действия входные и выходные кодовые слова представляются в различных формах. Такие устройства могут использоваться для преобразования кодовых слов из одной формы представления в другую.
По способу функционирования логические (цифровые) устройства (и их узлы) делятся на два класса: комбинационные цифровые устройства (КЦУ) и последовательностные цифровые устройства (ПЦУ). В КЦУ (цифровых автоматах без памяти) каждый символ на выходе определяется комбинацией символов на входах в текущий момент времени и не зависит от того, какие символы ранее действовали на этих входах, т.е. КЦУ не обладают памятью. В ПЦУ (цифровых автоматах с памятью) выходной сигнал определяется не только набором символов на входах в текущий момент времени, но и внутренним состоянием устройства, которое зависит от предыдущих значений символов на входах, т.е. ПЦУ обладают памятью.
Способы задания логических функций
Для задания логических функций используют два способа: табличный и аналитический.
При табличном способе строится таблица истинности, в которой приводятся все возможные значения наборов аргументов и значения логической функции, которые она принимает на каждом наборе. Число наборов аргументов N, т.е. число строк в таблице истинности, определяется по формуле 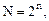 где n – число аргументов. Например, таблица истинности для логических функций одного аргумента приведена в таблице 3. Существует всего четыре функции одного аргумента.
где n – число аргументов. Например, таблица истинности для логических функций одного аргумента приведена в таблице 3. Существует всего четыре функции одного аргумента.
Таблица 3 – Таблица истинности для элементарных логических функций одного аргумента
| Аргумент X | Логические функции | |||

| 
| 
| 
| |
При n = 2 число наборов значений аргументов равно  а число функций
а число функций  Таблица истинности для логических функций двух аргументов представлена в таблице 4.
Таблица истинности для логических функций двух аргументов представлена в таблице 4.
Таблица 4 – Таблица истинности для элементарных логических функций двух аргументов
| Аргументы | Функции | ||||||||||||||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 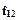
| 
| 
| 
|
Date: 2016-05-18; view: 585; Нарушение авторских прав