Градиенттің геометриялық мағынасы

Қарапайымдылық үшін екі тәуелсіз айнымалысы бар мақсат функцияны алайық:

z = F(x₁, х₂). (1)

Осы функцияның деңгей сызықтарын 1 суретте бейнлейміз.

Кейбір А нүктесін таңдап алып, ол үшін z мәнін есептейміз. Егер А нүктесінен әртүрлі бағыттағы бірдей қашықтыққа жылжыса, онда z функционалы әртүрлі шамасына өзгереді. Берілген нүктеден экстремумға тезірек жету үшін, z ең үлкен өзгеру бағытына жылжу керек.

1-сурет.

х₁ және х₂ айнымалылары арқылы z функцияларының дербес туындыларын табамыз (функцияны дифференциалдауда бір айнымалыдан басқалары тұрақтылар деп саналады). Бұл туындылар

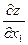және

арқылы белгіленеді.

А нүктесінің координаттарын дербес туындыларға арналған өрнекке қоямыз (басқа сөзбен айтқанда, берілген нүктеде олардың мәнін есептейміз). , шамасын аламыз.

Табылған сандарды кейбір вектордың ккоординаттары ретінде алып, осы векторды 2-суретте саламыз. Егер А нүктесі көрсетілген векторға параллель орналасқан түзудің бойымен орын ауыстырса, онда z жылдам өзгереді: вектрдың бағытымен өседі, кері қарай - кемиді. Бұл айнымалылар саны кез-келген функцияға да қатысты.

Кординатары ретінде z=F(x₁, x₂,..., х_п) функциясының x₁, x₂,..., х_п аргументтері бойынша алынған дербес туындысы қолданылатын вектор осы функцияның градиенті деп аталып,

арқылы белгіленеді.

Әрбір нүктеде градиент өзінікі болады. Ол өзінен әрқашан деңгей сызықтары (беттері) перпендикуляр өтетін берілген нүктеде функцияның ең үлкен өсу бағытын көрсетеді.

Сызықтық емес программалау есебін шешудің градиенттік әдісі осы қасиетке негізделген. Мүмкін болатын мәндер аймағынан А бастапқы нүктені іздеп, оның оптималды емес екеніне көз жеткізіп, ары қарай кездейсоқ емес, мақсатқа бағытталған әрекет жасаймыз. Бұл үшін берілген нүктеде вектордың координаттары – мақсат функцияның градиенттерін есептейміз

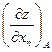, ,…, .Градиентке параллель А нүктесі арқылы өтетін түзудің параметрік теңдеуін құрамыз:

(2)

Максимумды табу кезінде түзу бойынша градиенттің бағытымен орын ауыстырамыз (t>0 деп аламыз); функционалды минимизациялау үшін қарама-қарсы жаққа қозғаламыз (t<0 деп аламыз). Осыдан келесі екі қозғалу әдістері болуы мүмкін.

1. Бастапқы нүктеден градиенттің бағытына мақсат функция өсуін тоқтатқанша жылжимыз. Бұл қозғалыс t параметрінің біртіндеп өсуі арқылы жүргізіледі, оның әрбір мәні үшін функционалдың мәні табылады, ал керек жағдайда қабылданатын шешімнің мүмкіндігі тексеріледі. Нүктенің осы бағытында жоғарғысына жетіп (1-суреттегі В нүктесі), градиентті қайта анықтаймыз және жаңа бағыт бойынша максималды мүмкін шамаға және т.б. орын ауыстырамыз.

Есептеудің осындай реті оңтайлы нүктеге жылдам көтерілуге сәйкес келеді және функционалдың мәнін градиентке қарағанда оңай есептеуге болатын кезде қолданылады.

Минимум есебінде қозғалыс функцияның кему жағына қарай жүреді және осындай әдіс жылдам түсу әдісі деп аталады.

2. Градиентке параллель сызықтың бойыгдағы бастапқы нүктеден t параметрінің мәнімен сипатталатын кейбір h аралығына орын ауыстырамыз. Екінші нүктеде өз градиентін анықтаймыз және анықталған бағыт бойынша h шамасына орын ауыстырамыз. Үшінші нүктені аламыз. Осыдан қайта градиент алып, келесі қадамды жасаймыз және т.б. Осылайша қозғалыстың бағытын анықтай отырып, функционалдың ең үлкен (ең кіші) мәніне ие нүктелерге жетеміз. Осы жағдайдағы траекторияның түрі 2-суретте көрсетілген.

2-сурет. 3-сурет.

Градиенттік әдіспен есептеудің екінші реті көптеген есептерде оптимумға біріншісіне қарағанда жылдам келтіріледі.Оптимумға жетудің белгісі градиенттің нолдік құрамын алу болып табылады.

Градиенттің бағытымен орын ауыстыру кезінде табылған нүкте есептің анықталған обылысынан тыс жатуы мүмкін (яғни, бұл қадамда облыстың аймақтары қиылысқан. Бұл жағдайда экстремум шекте табылады және оны іздеу күрделенеді. Соңғы қадамды жәй азайту арқылы облысқа қайтару (t параметрін азайту) тиімді емес, өйткені экстремалды нүктенің осы бағыттың шетінің қиылысында тұрғандығына сенімділік жоқ. Оптимум жаққа біруақытта қозғалту қажет.

3 суретті қарастырайық, мұндағы 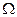мүмкін облыс қарайтылған сызықтармен, функционалдың деңгей сызықтары – жұқа сызықтармен берілген. А нүктесінен нормал бойымен деңгей сызықтарына орын ауыстырамыз (оның жанамасына перпендикуляр) және В нүктесі шектен тыс облысқа ауысамыз. Оптимумға М нүктесінде жететіндіктен, 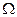облысына ВА сызығы бойынша қайта оралу пайдасыз.

Шектің қажетті аймағын деңгей сызықтарымен (4 сурет) қарастырамыз. А нүктесінде z₁ деңгей сызығына АР жанамысын жүргіземіз. В нүктесінде жаңа ВС орын ауыстыруын шектік сызықтың QP жанамасы оның қиылысу нүктесінде ВС –ға перпендикуляр болатындай етіп таң ап аламыз. Басқа сөзбен айтқанда, ВС шекке нормал болуы мүмкін. Сонда APQ және ABC бұрыштары тең болады, өйткені олардың қабырғалары өзара перпендикуляр. ВС жаңа бағыт бұрыңғы ВА-дан деңгей сызығы мен осы жердегі шек арасындағы бұрышқа шамаласа бұрышына ауытқиды. Ауытқу оптималды нүкте тұрған жаққа қарай болады.

4-сурет

Осылайша, егер В нүктесінен y_t =0 бұзылған шектік сызыққа нормал бойынша қозғалса, онда облысқа қайту оптимумға қажетті жақындаумен жүргізіледі.

y_i=0 сызығы 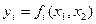функциясының деңгей сызығы болып табылады.Градиенттің деңгей сызығына нормалдылығын еске түсіріп, В нүктесінің шекке жақын екенін ескере отырып, облысқа қайту аймағы ретінде 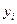функциясының В нүктесіндегі градиент бағытын алуға болады. Егер бірнеше шарттар бұзылса, В нүктесі үшін сәйкес функцияның градиенттерін тауып, оларды қосады. Алынған вектор қайту бағытын анықтайды.

С нүктесіне келіп, шекті қия отыраgrad z бағыты бойынша, ал D — да grad 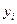бағытымен облысқа қозғаламыз және т.с.с.Қозғалыс шектерден тыс иректеліп қозғалады. Оптимумды алу белгісі ретінде нормалдардың деңгей сызығына және шек сызықтарына сәйкес келуі, яғни векторов grad z и grad 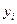векторларының коллениарлығы алынады. Ол аттары бірдей координаттарының пропорционалдығы немесе басқа әдістер арқылы тексеріледі. Есептеуді белгілі бір нақтылыққа жеткен кезде тоқтатады.

Процестің сәйкестігін жылдамдату үшін бір-екі иректен кейін АС немесе СЕ (4, 5 сурет) бағытында, яғни шекке параллель қадам жасалынады. Орын ауыстыру шамасын (t параметрі ) әдеттегіден үлкен етіп алады. Жаңа нүктеден оптимумға қарай иректелген қозғалыс басталады.

Шешімнің басқа ерекшеліктеріне тоқталмаймыз. Әрине, айтылғандардың барлығы кез-келген белгісіздердің санына қатысты.