Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Показательное (экспоненциальное) распределение. Функция надежности
|
|
Аналогом закона Пуассона для непрерывных случайных величин служит показательный (экспоненциальный) закон, функция плотности распределения которого имеет вид
где l > 0 – постоянный параметр.
Функция распределения (интегральная функция) показательного закона
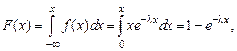
т. е.
Вероятность попадания случайной величины Х в интервал (a, b) составляет
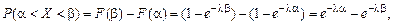
т. е.
Определим числовые характеристики показательного закона распределения:
математическое ожидание
дисперсия
среднее квадратичное отклонение
т.е. 
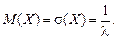
Если Т – непрерывная случайная величина, выражающая продолжительность времени безотказной работы какого-либо элемента, а l – интенсивность отказов (среднее число отказов в единицу времени), то продолжительность времени t безотказной работы этого элемента можно считать случайной величиной, распределённой по показательному закону с функцией распределения 
(l > 0), которая определяет вероятность отказа элемента за время t.
Функция надежности R (t) определяет вероятность безотказной работы элемента за время t: 
Date: 2016-05-16; view: 305; Нарушение авторских прав