H-образный металлодиэлектри-ческий волновод

H-образнная металлодиэлектрическая линия передачи рис. 2.8 представляет собой диэлектрическую пластину, ограниченную с двух сторон металлическими плоскостями. Здесь поле должно удовлетворять граничным условиям на поверхностях металлических пластин:

(2.56)

а также граничным условиям условиям для H- или E-волн на границах x=a и x=-a (см.параграф 2.2, 2.3).

Рис.2.8. Н-образный металлодиэлектрический волновод

Из волн типа E в такой структуре могут существовать только чётные волны, а из волн типа H – только нечётные.

Основной волной H-образной линии передачи является волна магнитного типа H₁₀, вектор которой имеет единственную составляющую, причём все составляющие векторов поля не зависят от координаты y. Эта волна полностью аналогична основной волне магнитного типа диэлектрической пластины; в частности, она имеет такую же фазовую скорость, как и волна типа H₁ диэлектрической пластины.

Все остальные типы волн H-образнной линии передачи имеют одну или несколько вариаций вдоль оси y. Характеристические уравнения для этих типов волн оказываются более сложными.

Задание: провести по аналогии с разделами 2.1, 2.2 все рассуждения для H - волн в H-образной линии передачи.

3. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИСПЕРСИОННОГО УРАВНЕНИЯ.

3.1. Вводные замечания.

В разд.2.4 дисперсионное уравнение (2.23) решается графически. Конечным результатом решения является дисперсионная характеристика (см. рис. 2.4,б), представляющая собой зависимость нормированной постоянной распространения для Е - и Н - мод от относительной толщины пленки . Графический способ прост, нагляден, однако обладает невысокой точностью и поэтому применяется редко.

Универсальными способами решений дисперсионных уравнений (2.26), (2.27), (2.32а)-(2.32г) являются численные методы решений нелинейных уравнений такого типа [10]. Ниже приводятся два метода: “половинного деления” (дихотомии) и аппроксимации. Алгоритм “половинного деления” является универсальным. Он позволяет получать решение с заданной точностью независимо от сложности дисперсионного уравнения, однако обладает медленной сходимостью. При сложном виде дисперсионного уравнения для повышения скорости вычислений целесообразно применить более быстро сходящиеся методы, в частности простой и наглядный метод аппроксимации.

Для численного решения рассмотренные выше характеристические уравнения в (2.17), (2.19) для Е - и Н - мод асимметричного волновода представим в виде

(3.1)

где для Н-мод , а для Е-мод ,1,2… – индекс моды.

В уравнении (3.1) следует брать главные значения арктангенсов. Дополнительные условия связи между коэффициентами h,p,q представим в виде (см.(2.19))

(3.2)

Подставляя уравнения (3.2) в (3.1) и отделяя линейную и нелинейную части, получим

, (3.3)

где

(3.4)

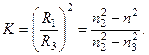
Уравнение (3.3) является нелинейным трансцендентным уравнением относительно параметра ; введенный параметр К характеризует степень асимметрии диэлектрического волновода.

Исходными данными при решении дисперсионного уравнения (3.3) являются длина волны , толщина волновода t, относительные диэлектрические проницаемости подложки, волноведущего слоя и покрытия 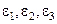соответственно (можно задавать и показатели преломления ), тип волны (Е или Н) и индекс m моды.

Определив из (3.3) параметр как искомое решение, находят далее величину , а затем из (2.25) – постоянную распространения и поперечные волновые числа p и q, что позволяет построить дисперсионную кривую (см. рис.2.4,б) и определить структуру соответствующей волны по формулам (2.17), (2.20).

В случае направляемых поверхностных волн коэффициенты h, p, q – положительные действительные числа. В соответствии с (3.2), (3.4) значение безразмерного параметра находятся в пределах

. (3.5)

3.2. Метод “половинного деления”.

В соответствии с (3.3) введем функцию :

. (3.6)

3.2.1. Алгоритм решения. Решением уравнения (3.3) являются такие значения , при которых функция . Поскольку в общем случае неизвестно, имеются ли такие решения на интервале [0,1], то более целесообразно искать не нуль функции , а некоторый малый интервал , в котором меняет знак. Такой интервал всегда можно найти, а затем сузить его настолько, чтобы выполнялось условие , где – заданная точность решения.

На рисунке 3.1 для иллюстрации метода представлена некоторая функция в интервале . При заданной точности определение корня алгоритма состоит из следующих шагов:

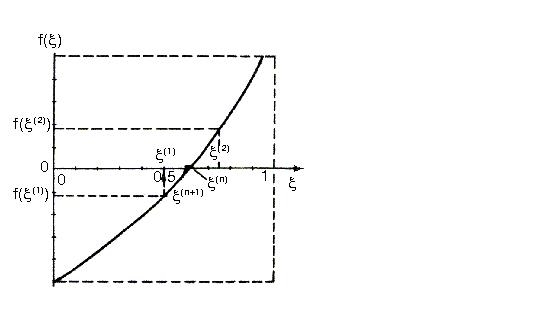
Рис. 3.1. К решению трансцендентного уравнения методом половинного деления.

1. Проверяют наличие корня уравнения (3.6) в заданном интервале. Если , то корней уравнения (3.6) нет, т.е. при выбранных исходных данных, заданном типе волны и индексе m моды волна в диэлектрическом волноводе не распространяется.

2. Меняя параметр m (номер моды), удовлетворяют условию .

3. Определяют “корень” на этапе первой итерации по формуле

(3.7)

и вычисляют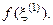

4. Проверяют условия: если 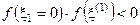, то сужают интервал поиска корня в пределах и определяют новый корень на втором этапе итерации, используя (3.7). Если же , то значение корня лежит в интервале .

5. Итерационная процедура последовательно повторяется nраз до выполнения условия . При этом значение корня рассчитывается по формуле

. (3.8)

Данный алгоритм позволяет вычислить значение с гарантированной точностью .

3.2.2. Программная реализация алгоритма по методу "половинного деления" (дихотомии) на алгоритмическом языке Фортран-90*⁾

Программа "beta1" предназначена для расчета поперечных волновых чисел h в волноведущем диэлектрическом слое для Н-волн планарного однородного изотропного диэлектрического волновода. Входными данными являются: alambda – длина волны 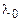; t – толщина волноведущего слоя; e1 – относительная диэлектрическая проницаемость покрытия; e2 – относительная диэлектрическая проницаемость волноведущего диэлектрического слоя; e3 – относительная диэлектрическая проницаемость 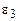подложки; m – номер моды. Программа определяет значение корня с заданной точностью eps. Выходной величиной является значение поперечного волнового числа h. Размерности метрических переменных следует брать одинаковыми.

!--------------------------------------------------------------

!Программа расчета волнового числа h в волноводном

!диэлектрическом слое для H-волн планарного однородного

!изотропного диэлектрического волновода

Program beta1

!переменный, общие для beta1 и функции f

common /cblock/ a,ak,m

!входные данные; при указанных значениях

!результат для контроля: h = 0.8956242

!длина волны; размерности alambda и t одинаковые

alambda = 0.85

!толщина волноведущего слоя

t = 5.

!отн. диэл. проницаемость покрытия

e1 = 2.11

!отн. диэл. проницаемость волноведущего слоя

e2 = 2.14

!отн. диэл. проницаемость подложки

e3 = 2.12

!номер моды

m = 1

!погрешность значения корня

eps = 1e-6

!вычисляется коэффициент A

a = 2 * sqrt(e2-e3) * t/alambda

!вычисляется коэффициент K

ak = (e2-e1) / (e2-e3)

!обращение к функции решения уравнения F(x)=0

aksi = dih(1e-10,1.,eps)

!определение h

h = aksi * 2*3.14159/alambda * sqrt(e2-e3)

!вывод результата

print *, h

End

!--------------------------------------------------------------

!Функция решения уравнения F(x)=0 методом дихотомии

!с точностью eps при условии, что корень лежит в

!интервале от a до b

Date: 2016-05-16; view: 679; Нарушение авторских прав