Исходные соотношения строгой электродинамической теории

Пленочные диэлектрические волноводы имеют некоторые общие черты с полыми металлическими волноводами. В частности, и те и другие могут поддерживать ограниченное число направленных типов волн-мод на любой заданной частоте; в обеих структурах возможно преобразование мод, если форма волновода отклоняется от идеальной прямолинейной и т.п. В тоже время имеется и существенные различия, вызванные в первую очередь тем, что электромагнитное поле поле существует строго внутри металлических волноводов, а в ДВ оно формально существует во всём пространстве.

Исследуем направляемые (волноводные) моды на примере планарного регулярного диэлектрического волновода (рис 2.1, а-б). Для простоты далее будем полагать, что волновод является бесконечно протяженным в направлении оси OY и изменения поля в этом направлении нет, то есть .

Рис 2.1.Планарный диэлектрический волновод

Ограничимся случаем монохроматического поля с временной зависимостью , где –круговая частота. Для определения структуры электромагнитного поля волн диэлектрического волновода необходимо решить систему уравнений Максвелла:

, , (2.1)

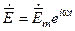где и , – абсолютная диэлектрическая и магнитная проницаемость

с граничными условиями на поверхностях раздела x=0, x=t и физическим условием убывания поля при .

Каждое из уравнений (2.1) равносильно трем скалярным уравнениям:

; (2.2)

;

(2.3)

В соответствии с методом комплексных амплитуд 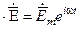, где – комплексная амплитуда. После сокращения в (2.2), (2.3) на получим уравнения для комплексных амплитуд.

Задание: из уравнений Максвелла получить (2.5), (2.6).

Поскольку в направляющих линиях необходимо передавать энергию из одного сечения в другое в виде бегущих в направлении осиOZ волн, которые характеризуются множителем бегущей волны , то аналогично случаю полых металлических волноводов решение (2.2), (2.3) для комплексных амплитуд ищем в виде:

, (2.4)

где - комплексные амплитуды, зависящие только от x Г,1/м – коэффициент распространения волны в рассматриваемой структуре.

После подстановки (2.4) в (2.2), (2.3) последние разделяется на две следующие независимые подсистемы:

(2.5) (2.6)

Из (2.5), (2.6) следует, что для рассматриваемого случая моды делятся на волны типа H: , определяемые уравнением (2.5), для которых отличны от нуля только составляющие , и на волны типа E: , определяемые уравнением (2.6), для которых отличны от нуля только составляющие .

Таким образом, для определения структуры возможных типов электромагнитных волн волн в диэлектрическом пленочном волноводе достаточно найти продольную (вдоль оси OZ) – компоненту для H - волн или -компоненту для E - волн, поскольку поперечные компоненты затем можно вычислить, используя (2.5), (2.6). Из уравнений (2.5), (2.6) видно, что для определения структуры электромагнитных волн в диэлектрическом волноводе удобно использовать компоненты – компоненту для H – волн и –компоненту для E - волн.

Задание: пояснить последнее утверждение.

Известно, что каждая из компонент электромагнитного поля в каждой из областей на рис.1.2,б удовлетворяет однородному волновому уравнению

(2.7)

с соответствующими граничными условиями на поверхностях разделов и условию убывания при ; полагалось, что В (2.7) – волновое число свободного пространства ( – длина волны); – оператор Лапласа; – относительная диэлектрическая проницаемость сред.

Волны H-типа в асимметричном планарном диэлектрическом волноводе.

Исключив составляющие и из системы уравнений (2.5), для H - волн, приходим к последующим скалярным уравнениям для в каждой из сред (рис. 2.1,б):

, при (2.8а)

где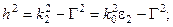

, при x 0, (2.8б)

где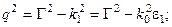

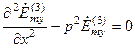, при x t, (2.8в)

где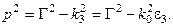

Задание: для рассматриваемого случая раскрыть (2.7) для , и сравнить с (2.8).

Отличие записи (2.8,а) от (2.8,б), (2.8,в) обусловлено тем, что электромагнитные волны, определяемые вне диэлектрического слоя должны иметь характер поверхностной волны (см. (1.2)), т.е. поле как бы “прилипает” к поверхности раздела и амплитуда уменьшается при удалении от нее по экспоненциальному закону. Величины h, p, q при записи (2.8,а) – (2.8,в) – вещественные положительные числа.

На границе раздела раздела (рис. 2.1,б) тангенциальные составляющие электрического и магнитного поля должны удовлетворять граничным условиям (на границе раздела двух сред касательные компоненты электрического и магнитного поля непрерывны):

(2.9)

Запишем решение уравнений (2.8,а) – (2.8,в) с учетом условия убывания поля при :

(2.10)

где A_н , B, C, D и q, h, p – постоянные, которые нужно определить.

Задание: пояснить подробно (2.10), опираясь на общий вид решения (2.8,а) – (2.8,в).

Подставляя (2.10) в граничных условия (2.9) для получаем соотношения:

(2.11).

Кроме того, в соответствии с (2.5) . Найдем помощью (2.10) составляющую и удовлетворим граничным условиям (2.9). В результате получим дополнительную к (2.9) систему уравнений:

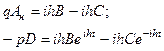(2.12).

Четыре линейных однородных уравнения связывают четыре неизвестные постоянные A_н, B, C, D. После преобразования (2.11), (2.12) к стандартной форме однородных алгебраических уравнений, для получения отличных от нуля решений необходимо приравнять к нулю определитель системы уравнений (2.11), (2.12):

Задание: объяснить последнее утверждение.

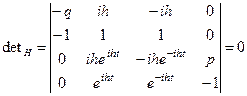. (2.13)

Раскрывая соотношение (2.13), называемое характеристическим уравнением H–мод, имеем

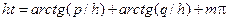, (2.14)

где m = 0,1,2,3… – индекс мод.

Задание: получить (2.14) { при выводе (2.14) использовать формулу }.

Поскольку тангенс – функция периодическая с периодом, равным , в правой части соотношения (2.14) появилось целое кратное числа . Таким образом, при данной толщине диэлектрического волновода t существует множество решений (типов волн – мод) характеристического уравнения (2.14). Эти моды различаются индексом m, различными значениями поперечных волновых чисел h, q, p и обозначаются как Н₀, Н₁, Н₂ и т.д.

Учитывая дополнительные соотношения, следующие из (2.8,а) – (2.8,в):

; , (2.15)

исключая в них постоянную распространения , можно получить еще два уравнения, которые связывают h, q, p.

Обозначим через коэффициент преломления среды ( = 1,2,3), получим полную систему уравнений, определяющих значения поперечных волновых чисел h, q, p для H– мод:

(2.16)

Выразив из (2.11), (2.12) амплитудные коэффициентыB, C, D через A_н и подставив их в (2.10), найдём комплексные амплитуды составляющих H–мод через произвольную амплитудную постоянную A_н (зависит от источника возбуждения, который на данном этапе не рассматривается) и поперечные волновые числа h, q, p:

Задание: получить (2.17).

(2.17).

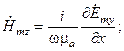
Определив из системы (2.16) величины h, q, p, зависящие от толщины ДВ t и от коэффициентов преломления сред, можно полностью рассчитать электромагнитное поле любой H –волны по формуле (2.17). Постоянная распространения находится с помощью соотношений (2.15); длина волны в диэлектрическом волноводе , а фазовая скорость .

Комплексная постоянная A_н осталась не определённой, поскольку исследуются “свободные”, т.е. не зависящие от источника возбуждения, волны. Модуль и фаза постоянной A_н зависят от амплитуды и фазы источника возбуждения. Используя (2.17) и учитывая (2.4), можно найти структуру H – мод в направлении распространения волн, например:

где – комплексная амплитуда. Откуда видно, что в фиксированный момент времени вдоль оси ДВ распределение –компоненты носит периодический характер с периодом, равным длине волны в диэлектрическом волноводе .

2.3. Волны E–типа в асимметричном планарном диэлектрическом волноводе

По аналогии с разд. 2.1, 2.2, выполняя все задания, будем исследовать E-моды в диэлектрическом планарном волноводе. Единственными ненулевыми составляющими поля в этом случае будут ; граничные условия отличаются от (2.9).

Решение ищется в виде [сравни с (2.10)]:

(2.18)

Характеристическое уравнение и соотношение между постоянными h, q, p выводятся так же, как и для H - мод, однако следует иметь в виду, что диэлектрические проницаемости слоёв различные. В результате получим систему уравнений, определяющих постоянными h, q, p для E - мод:

. (2.19)

Эти уравнения отличаются от уравнения (2.16) для H–мод только наличием квадрата отношений показателей преломления в аргументах арктангенса; E–моды обозначаются как и т.д.

Составляющие поля для E - мод записываются с учетом (2.6) следующим образом:

(2.20)

, .

Классификация мод в планарном диэлектрическом волновод

В асимметричном планарном волноводе (рис. 2.1,а,б) для показателей преломления , как правило, выполняются условия: . Поэтому соотношения

(2.21)

представляют собой в системе координат (q, h), (p, h) уравнения окружностей с сильно различающимися радиусами R_q и R_p (рис. 2.2,а). Отсюда q>>p и q>>h при любых h. Кроме того, и .

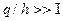Теперь рассмотрим зависимость : при угол . Поскольку и , последние уравнения в (2.16), (2.19) можно привести к следующему виду:

для H - мод ; (2.22)

для E - мод .

Так как , система уравнений для H – и E - мод асимметричного волновода с учетом (2.21), (2.22) примет вид

;

;

. (2.23)

В рассматриваемом приближении H– и E - моды сильно асимметричном волноводе вырождены, т.е. поперечные волновые числа h, q, p для m-й моды одинаковы в случае H - и E - мод.

Поперечное волновое число q однозначно находится из первого выражения в (2.23). Систему двух последних трансцендентных уравнений (2.23) относительно h и p можно решить (при желании получить большую точность) одним из численных методов (см. разд. 3), либо более наглядным и простым графическим методом (однако, он обладает сравнительно невысокой точностью).

Решения двух последних уравнений (2.23) представлены на рис. 2.2,б графически на плоскости pt–ht. Совместное решение этих уравнений есть точки пересечения двух кривых, соответствующие модам пленочного волновода. Поскольку величина p должна быть положительной [см. (2.10),(2.18)], следует ограничиться только первым квадрантом (рис. 2.2,в поясняет это). Как следует из рис.(2.2,б), при распространяющихся волноводных мод не существует. Только когда частота колебаний (или разность показателей преломления) становится настолько большой, что , круг радиуса впервые пересекает ветвь m=0 кривой. Это – решение системы из двух последних уравнений (2.23) для m=0; оно описывает в рассматриваемом приближении и - волны, которые являются основными волнами плоского несимметричного диэлектрического волновода. Из выражения для видно, что число волноводных мод зависит от параметров, которые можно изменять, а именно . Так, при в волноводе, кроме – и -мод, распространяются еще две моды и и т.д. Радиус окружности (следовательно, и значение ) для m-й моды должен лежать в пределах

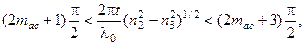(2.24)

где

Соотношение (2.24) позволяет, зная параметры , найти число распространяющихся мод в волноводе или, наоборот, подобрать эти параметры, исходя из требований.

Найденные значения ptи ht позволяют определить с учетом (2.15) постоянную распространения Г, фазовую скорость и длину волны в линии , а также все компоненты поля из выражений (2.17) или (2.20), т.е., по существу, решить задачу о нахождении мод в планарном асимметричном диэлектрическом волноводе.

На рис.2.3 в качестве примера показано распределение компоненты поля –волн в диэлектрическом волноводе в случае выполнения для каждой моды условия (2.24). Порядок m волны равен, как видно, числу нулей в поперечном распределении поля.

Рис 2.3. Распределение компоненты поля

Удобно для исследования дисперсионных характеристик ДВ (зависимости продольного волнового числа Г от частоты ) записать характеристические уравнения (2.16), (2.19) в виде, непосредственно связывающем Г с параметрами сред и с частотой. Из (2.15) следует, что

(2.25)

где , с- скорость света.

Подставляя (2.25) в (2.16) и (2.19), получаем для симметричного волновода в случае Н - мод

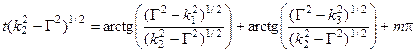(2.26)

и, соответственно, в случае Е - мод

. (2.27)

Соотношения (2.26), (2.27) представляют собой дисперсионные уравнения и при заданных позволяют проследить зависимость Г от для каждой Н - и Е - моды порядка m. Пример численного решения этих уравнений дан на рис.(2.4,а,б), где – относительная толщина пленки, – эффективный показатель преломления.

Рис.2.4. Дисперсионные кривые.

Численные методы решения дисперсионных уравнений с их программной реализацией рассмотрены в разделе 3. Несовпадение кривых для Н - и Е - мод с одинаковым индексом m вызвано тем, что уравнения (2.21), исследованные ранее (см. кривые на рис.2.2), были получены при упрощающих предположениях. Однако в изотропных диэлектрических волноводах это различие невелико и практически трудно получить одномодовый режим (единственная волна Н₀).

Поскольку в случае направляемых поверхностных мод постоянные h,q,p – положительные действительные величины, то из (2.25) следует, что

где При в соответствии с (2.17), (2.20) волна представляет собой экспоненциальную функцию во всех трех областях (рис. 2.5,а), так что поле неограниченно возрастает вне диэлектрического волновода.

Рис. 2.5. Структура поля для различных режимов

Такое решение физически бессмысленно и практически нереализуемо. Соответственно на графике, приведенном на рис. 2.4,а, .

При из (2.17), (2.20) следует, что волна представляет собой гармоническую функцию в области n₂ и убывает по экспоненциальному закону в областях n₃ (подложки) и n₁ (покрытия) (см. рис.2.1). Поскольку энергия, переносимая такими типами волн, сосредоточена вблизи волноводного слоя n₂, эти волны называются поверхностными (волноводными). Два таких решения показаны на рис.2.5,б,в.

При поле (2.17), (2.20) имеет экспоненциально убывающий характер в области n₁и гармонический в областях n₁, n₃.Такие волны не удовлетворяют физическому условию убывания при x и соответствуют так называемым излучательным модам подложки (рис. 2.5,г). Тогда на графике, приведенном на рисунке 2.4,а нижняя граница отношения .

Наконец, при структура волны становится гармонической во всех трех областях (рис.2.5,д), что соответствует излучательным модам волновода.

Физический смысл ограничений (2.28) состоит в том, что фазовая скорость мод должна быть не больше плоских волн, распространяющихся в материале подложки с показателем преломления n₃, и не меньше плоских волн в волноводном слое с показателем преломления n₂.

Моды в симметричном планарном диэлектрическом волноводе

В симметричном волноводе (см. рис. 2.1,в) n₁=n₃. Из первых двух уравнений в (2.16), (2.19) следует, что при n₁=n₃имеем p=q. Подставив p=q и n₁=n₃ в последнее уравнений (2.16) и (2.19) и сделав для удобства замену t=2d, получим:

для Н-мод (2.29)

для Е- мод

Тогда характеристические уравнения для симметричного волновода толщиной t=2d будут иметь вид

для Н- и Е-мод

(2.30а)

Н-моды, (2.30б)

Е-моды. (2.30в)

Как и в случае асимметричного планарного диэлектрического волновода, систему трансцендентных уравнений (2.30,а), (2.30,б) или (2.30,а), (2.30,в) можно решить графически (рис. 2.6,а), причем в случае симметричного волновода решение допускают все значения m_c=0,1,2,3..., как четные, так и нечетные (рис.2.6,б).

Для нахождения распределения поля в симметричном волноводе, удобнее сдвинуть систему координат к средней плоскости пленочного волновода (рис.2.1,в): . Тогда с учетом сказанного выше для области [сравни с (2.17), (2.20)]

Н-моды (2.31а)

Е-моды (2.31б)

Выражение (2.31) поясняет смысл четности и нечетности мод в симметричном планарном волноводе относительно координаты x, приведенной на рисунке 2.1,в.

Рис 2.6. К графическому решению системы уравнений в случае симметричного волновода

Задание: записать все компоненты четных и нечетных Н - и Е - мод, используя (2.17), (2.20).

Дисперсионные уравнения для четных и нечетных мод в симметричном пленочном волноводе можно вывести из (2.26), (2.47), учитывая особенности симметричного волновода (n₁=n₃, k₁=k₃),

- четные Н-моды; (2.32а)

- нечетные Н- моды; (2.32б)

- четные Е-моды; (2.32в)

- нечетные Е- моды, (2.32г)

где все обозначения аналогичны обозначениям в (2.26), (2.27).

На примере симметричных пленочных волноводов отметим еще раз особенности рассматриваемых диэлектрических и металлических волноводов.

Во-первых, новая волна, появляющаяся в диэлектрическом волноводе, на критической частоте (см. рис. 2.4,а; 2.6,б) имеет волновое число p=q=0 и в соответствии с (1.25) . Таким образом, волна распространяется со скоростью равной фазовой скорости плоской волны в безграничной среде с параметрами, совпадающими с параметрами среды, окружающей диэлектрический волновод. В то время как в металлическом волноводе при критической частоте =0.

Во-вторых, при частоте ниже критической в диэлектрическом волноводе моды данного типа вообще не существуют, а в металлическом волноводе она существует в виде затухающей волны.

По аналогии с (2.24) (используя рисунок 2.26) можно записать условие, позволяющее найти число распространяющихся Н- и Е - мод в симметричном диэлектрическом пленочном волноводе, зная параметры :

где m _c =0,1,2… (2.33)

Волны в планарном диэлектрическом волноводе на металлической подложке

Данная линия передачи показана на рис 2.7. Волновод попрежнему является бесконечно протяженным в направлении оси OY и изменения поля в этом направлении нет, то есть .

Рис 2.7. Планарный диэлектрический волновод на металлической подложке.

Для определения структуры электромагнитного поля и основных характеристик полагаем металлическую подложку идеально проводящей, используем уравнения электродинамики (2.2), (2.3), представление бегущих волн вдоль оси z (2.4) в виде E- и H-волн (2.5), (2.6) соответственно.

Волны E-типа в планарном диэлектрическом волноводе на металлической подложке.

Исключив составляющие и из системы уравнений (2.6), для H - волн, приходим к последующим скалярным уравнениям для в каждой из сред (рис. 2.7):

, при

где

, при x>t, (2.34)

где

Общее решение уравнений (2.34) с учетом условия убывания поля при по аналогии с (2.18) имеет вид:

(2.35)

Для определения постоянных , B, С, h, p воспользуемся граничными условиями аналогичными (2.9). Тогда, учитывая, что первая среда (подложка) является идеальным проводником:

. (2.36)

При этом в соответствии с (2.6)

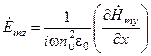, , где . (2.37)

Подставляя (2.37) в граничное условие и учитывая (2.35), получаем 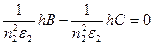, т.е. В=С.

Тогда общее решение (2.35) волнового уравнения принимает вид

(2.38)

где 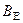– некий новый коэффициент.

Из двух оставшихся граничных условий в (2.36) получаем

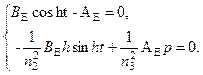(2.39)

Система (2.39) для определения отличных от нуля коэффициентов совместна, если

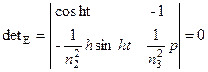. (2.40)

Раскрывая соотношение (2.40), получаем характеристическим уравнением дляE– мод в планарном диэлектрическом волноводе на металлической подложке

, где m = 0,1,2,3… – индекс моды. (2.41)

Задание: объяснить (2.40) и получить (2.41).

Кроме того в соответствии с (2.34)

. (2.42)

Выражая через из (2.39), учитывая с (2.38) и (2.37), получаем следующее представление для компонент электромагнитного поля:

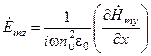, , где . (2.43)

Из (2.43) следует, что в рассматриваемой структуре могут существовать Е -волны и т.д. (индекс моды m = 0, 1, 2…), поскольку в соответствии с (2.36) электрическое поле в диэлектрической пленке на металлической подложке должно удовлетворять граничным условиям на поверхности металла.

Задание: пояснить последнее утверждение.

Задание: Используя (2.41), (2.42) записать условие, аналогичное (2.33), позволяющее найти число распространяющихся Е - мод в планарном диэлектрическом волноводе на металлической подложке, зная параметры .

2.6.2. Волны H-типа в планарном диэлектрическом волноводе на металлической подложке.

По аналогии с 2.6.1 будем исследовать H -моды в диэлектрическом планарном волноводе на металлической подложке. Единственными ненулевыми составляющими поля в этом случае в соответствии с (2.5) будут . Снова решение ищется в виде (сравни с (2.35)):

(2.44)

Характеристическое уравнение и соотношение между постоянными h, p выводятся так же, как и для E - мод:

, где m = 0,1,2,3… – индекс моды,

. (2.45)

Соответствующие компоненты электромагнитного поля для H-мод имеют вид:

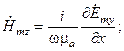
(2.46)

Задание: провести по аналогии с разделом 2.6.1. все рассуждения для H - волн.

Из (2.46) следует, что в рассматриваемой структуре могут существовать H-волны и т.д. (индекс моды m =1, 2, 3…), но m ≠0 поскольку в соответствии с (2.36) электрическое поле в диэлектрической пленке на металлической подложке должно удовлетворять граничным условиям на поверхности металла.

Задание: Используя (2.45) записать условие, аналогичное (2.33), позволяющее найти число распространяющихся H - мод в планарном диэлектрическом волноводе на металлической подложке, зная параметры .

Мощность, переносимая модой по диэлектрическому планарному волноводу.

2.7.1. Переносимая мощность. Выражения для полей, направляемых пленкой Н - и Е - мод (2.17), (2.20) позволяют определить среднюю мощность, переносимую отдельной модой вдоль оси Z на единичную ширину в направлении Y (см. рис. 2.1,б).

Задание: получить последовательно(2.47) – (2.50).

В частности для Н-мод с учетом (2.6,а)

(2.47)

где – комплексный вектор Пойнтинга; ( единичный орт оси Z).

Подставляя в (2.34) выражения для из (2.17), находим

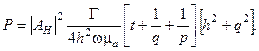(2.48)

Для Е- мод с учетом (2.6)

(2.49)

Подставляя в (2.49) выражение для из (2.20), находим

. (2.50)

2.7.2. Соотношения ортогональности направляемых мод. Учитывая (2.47), (2.49) можно показать, что для Н - мод имеет место соотношение

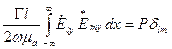, (2.51)

где – индексы двух различных мод; – символ Кронекера, который равен нулю для и единице для .

Из (2.51) следует, что при левая часть равна мощности, переносимой вдоль пленочного волновода (с единичной шириной вдоль направления Y) модой ; при правая часть равна нулю. Физическая суть этого в том, что различные моды в процессе распространения не обмениваются энергией (не взаимодействуют).

Соответственно для Е-мод

. (2.52)

Соотношение (2.51), (2.52) представляют собой так называемые соотношения ортогональности между двумя модами в диэлектрическом волноводе без потерь.

Задание: получить (2.51) или (2.52).

2.8. Затухание в диэлектрическом волноводе.

Анализ Н- и Е-мод в планарном диэлектрическом волноводе проводился в предположении, что диэлектрик является идеальным (без потерь). При этом в режиме направляемых поверхностных мод (волноводных мод), определяемом условием (2.28), коэффициент распространения – действительная величина. Наличие диэлектрических или магнитных потерь в материале диэлектрического волновода (подложки, покрытия) вызовет преобразование части электромагнитной энергии, переносимой волной, в тепловую энергию. Можно предположить, что для планарного диэлектрического волновода с потерями за счет конечной проводимости диэлектрических сред зависимость полей от координаты Z имеет формально тот же вид, что и для случая без потерь (2.4). Однако при этом является комплексной величиной: . Поэтому любая составляющая поля в соответствии с (2.4) будет изменяться по закону 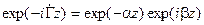, где – величина, характеризующая убывание произвольной составляющей электромагнитной волны вдоль оси Z ( –коэффициент затухания, –коэффициент фазы).

Так как средняя мощность Р (2.48), (2.50) пропорциональна квадрату амплитуды поля, то , где Р₀ – средняя за период мощность в сечении z=0 диэлектрического волновода.

Разность между мощностями в сечении z и равна мощности потерь на отрезке волновода длиной : . Разделив обе части равенства на и устремив к нулю, найдем значение мощности тепловых потерь, приходящееся на единицу длины:

, откуда , (2.53)

где – коэффициент затухания, 1/м.

Мощность Р, переносимая вдоль планарного диэлектрического волновода с Н- и Е-модами, определяется соотношениями (2.47) – (2.49). Средняя за период мощность тепловых потерь 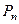находится из выражения

, (2.54)

где интегрирование ведется по всему объему, заполненному диэлектриком с потерями, при единичной длине в направлении Y, при этом в зависимости от области подставляется соответствующее значение (i=1,2,3).

Задание: пояснить формулу (2.54), используя уравнение баланса для средней за период мощности (см. например, [3], [4]).

В заключение отметим следующие три обстоятельства. Во-первых, поскольку определяется отношением 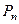к мощности Р, переносимой вдоль планарного диэлектрического волновода, то интегрирование выражений (2.49), (2.50), (2.54) по переменной y можно производить не в бесконечных пределах, а по отрезку единичной длины. Во-вторых, при вычислении 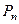и Рпредполагается, что структура Н- и Е-мод в диэлектрическом волноводе приблизительно совпадает со структурой этих волн в среде без потерь. В-третьих, если исследуется диэлектрическая пластина на металлический подложке (см. рис.2.17), то необходимо учитывать среднюю мощность тепловых потерь в металле, которая рассчитывается аналогично случаю металлических волноводов:

, (2.55)

где – касательная составляющая магнитного поля на металлической поверхности; – удельное поверхностное сопротивление металла, Ом ( - проводимость металла). Подставляя в формулу (2.47), (2.49), (2.54) выражения для соответствующих компонент Н- или Е-мод (2.17), (2.20) или (2.29), находим выражение для коэффициента затухания (2.53) в диэлектрическом планарном волноводе. Очевидно, что при конкретных расчетах необходимо сначала определить волновые числа h, p, q (р, h) с помощью численных методов (см. разд.3).

Date: 2016-05-16; view: 775; Нарушение авторских прав