Точки, которые разделяют промежутки выпуклости и вогнутости называются точками перегиба функции

Схема исследования функции на выпуклость, вогнутость:

1. Находим вторую производную функции (это производная от первой производной).

2. Находим точки, в которых вторая производная равна нулю или не существует.

3. Исследуем знаки второй производной справа и слева от найденных точек.

Для примера исследуем на выпуклость, вогнутость функцию

1. Найдем первую производную функции :

2. Найдем вторую производную функции .

3. Найдем нули второй производной:

- точка перегиба.

Найдем знаки второй производной и определим промежутки выпуклости, вогнутости функции:

График нашей функции выглядит так:

Мы видим, что слева от точки функция выпуклая (если представить, что мы "поливаем" график водой, то она с него скатывается - неспроста на этом промежутке вторая производная отрицательная).

Справа от точки функция вогнутая. (На этом промежутке вода как бы накапливается - здесь вторая производная больше нуля)

Полное исследование функции:

Итак, давайте, для примера, исследуем функцию и построим ее график.

1. Найдем ОДЗ

Сразу отметим, что при знаменатель дроби равен нулю, следовательно, прямые и являются вертикальными асимптотами графика функции .

2. Исследуем функцию на четность.

Получили, что , следовательно, функция - нечетная, и график функции симметричен относительно начала координат.

3. Найдем точки пересечения с осями координат.

а) Точки пересечения с осью ОХ (y=0)

б) Точка пересечения с осью ОY (x=0)

График нашей функции проходит через начало координат.

4. Найдем промежутки знакопостоянства.

Решим неравенство

Воспользуемся методом интервалов.

Найдем корни числителя и знаменателя, нанесем их на числовую ось и расставим знаки:

Корень числителя:

Корни знаменателя: ;

Расставим знаки:

Итак, при и

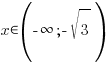при и

5. Найдем промежутки возрастания-убывания функции и экстремумы.

а) Найдем производную функции

б) Приравняем производную к нулю:

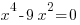
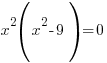
(корень четной кратности); ;

Корни знаменателя - - также корни четной кратности.

В корнях четной кратности производная знак не меняет.

в) Нанесем нули производной и корни ее знаменателя на числовую ось, расставим знаки и найдем точки экстремума и промежутки возрастания и убывания.

Итак, мы нашли промежутки возрастания и убывания.

Найдем значение функции в точках экстремума:

Заметим, что, поскольку функция 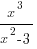нечетная, и мы нашли, что , мы могли бы сразу написать, что

Итак, отметим в нашей координатной плоскости точки минимума и максимума функции и точку пересечения графика функции с осями координат.

На рисунке ниже большими красными кружками обозначены точки, через которые проходит график функции.

Теперь учтем промежутки возрастания-убывания и промежутки знакопостоянства функции (п. 4) и построим ее график. Помним, что график функции не пересекает абсциссы, он лишь приближается к ним!

Date: 2016-05-16; view: 641; Нарушение авторских прав