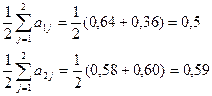Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример применения критерия Лапласа
|
|
Для условий примера из п.2.7 (табл.2.2) использование критерия Лапласа будет выглядеть следующим образом:
1. Найти среднее арифметическое значение исходов по каждому проекту. Оно является оценкой альтернативы по критерию Лапласа:
L1 = (x11+x12+x13)/3 = (45+25+50)/3 = 40
L2 = (x21+x22+x23)/3 = (20+60+25)/3 = 35
2. Сравнить рассчитанные величины и найти альтернативу с максимальным значением критерия:
40 > 35 => L1 > L2 => X* = X1
По критерию Лапласа оптимальным является проект Х1, у которого наибольшая средняя прибыль.
Среднее значение является достаточно популярной мерой в условиях неопределенности и даже риска, однако оно не учитывает разброс результатов относительно этого значения. Так, например, альтернативы А{400; 600} и В{0; 1000} являются эквивалентными по критерию Лапласа (LA = LB = 500), однако альтернатива В более "рискованна", так как предполагает возможность при плохом стечении обстоятельств не получить ничего.
Критерий Лапласа
Дата добавления: 2014-11-01; просмотров: 478; Нарушение авторских прав
Для обоснования критерия Лапласа в задачах принятия решений в условиях неопределенности воспользуемся следующими соображениями, отражающими основную суть принципа недостаточного обоснования. Так нам не известны вероятности пребывания рассматриваемой системы в каждом из ее m вероятных состояний, то мы не имеет достаточно оснований сделать утверждение о различии этих вероятностей. В противном случае имела бы место ситуация принятия решения в условиях риска. Скорее, мы можем предположить равенство вероятностей реализации любых возможных состояний изучаемой системы. Таким образом, исходную задачу можно рассматривать как задачу принятия решений в условиях риска, когда выбирают решение, обеспечивающее наибольший ожидаемый результат, то есть:
Здесь предполагается, что вероятности пребывания рассматриваемой системы во всех возможных состояниях одинаковы и равны 1/m. Данный критерий называют критерием Лапласа. Этот критерий не слишком хорош, ибо трудно предположить, что все состояния равновероятны. Пример 1. В отдел технической экспертизы поступило на рассмотрение два проекта выпуска одного и того же изделия. Проекты ориентированы на различный объем выпуска изделия. По предварительным прогнозам емкость рынка может составить a или b единиц данного изделия. Для каждого из этих возможных емкостей рынка, существует наилучший с точки зрения прибыли проект выпуска. Матрица выигрышей в условных денежных единицах приведена ниже:
В данном случае n=m=2. Тогда имеем:
Таким образом,
и наилучшим проектом выпуска в данной ситуации в соответствии с критерием Лапласа будет второй проект. |
Date: 2016-05-15; view: 641; Нарушение авторских прав