Функция полезности. В теории полезности исходят из того, что критерий эффективности предназначен для выявления порядка предпочтений на альтернативах (исходах операции)

В теории полезности исходят из того, что критерий эффективности предназначен для выявления порядка предпочтений на альтернативах (исходах операции), что позволяет обеспечить обоснованный выбор решений.

Выявить формально отношение предпочтения или безразличия непосредственным сравнением альтернатив трудно: показатели исходов операции многочисленны, имеют разный физический смысл и разные шкалы измерений (стоимость изготовления, численность обслуживающего персонала, пропускная способность, вероятность прохождения сигнала и т.д.). Деньги тоже не выступают универсальной мерой ценности. Вводится искусственная мера, которая определяется через полезность альтернатив (исходов). Чаще всего это действительное число, приписываемое исходу операции и характеризующее его предпочтительность по сравнению с другими альтернативами относительно цели.

Зная возможные альтернативы с их показателями полезности, можно построить функцию полезности, которая дает основу для сравнения и выбора решений.

Функция полезности представляет собой числовую ограниченную функцию , определенную на множестве альтернатив , так, что , когда альтернативы и неразличимы и , когда альтернатива предпочтительней альтернативы .

В зависимости от типа показателей исходов операции функция полезности может быть либо непрерывной, либо дискретной.

Функцию полезности называют прямой, если чем больше значение показателя исхода операции, тем он полезнее, и обратной, если больше значение показателя исхода операции, тем он менее полезен.

Определение полезности как меры оценки того или иного исхода операции представляет сложную задачу, точные методы решения которой пока не найдены.

14.6.2. Оценка сложных систем в условиях риска на основе функции полезности

Операции, выполняемые в условиях риска, называются вероятностными. Это означает, что каждой альтернативе ставится в соответствие не один, а множество исходов с известными условными вероятностями появления .

Эффективность систем в вероятностных операциях находится через математические ожидания функции полезности на множестве исходов

При исходах с дискретными значениями показателей

При исходах с непрерывными значениями

,

где – условная плотность вероятностей исходов.

Критерий оптимальности для вероятностных операций имеет вид:

Кроме операции «в среднем» рассмотренной выше используются и другие критерии оценки систем:

– максимум вероятности случайного события;

– минимум среднего квадрата уклонения результата от требуемого;

– минимум дисперсии результата;

– минимум среднего (байесовского) риска;

– максимум вероятностно – гарантированного результата.

14.7. Оценка сложных систем в условиях неопределенности

В большом классе задач управления организационно–техническими системами отсутствуют объективные критерии оценивания достижения целевого и текущего состояний объекта управления, а также статистика, достаточная для построения соответствующих вероятностных распределений (законов распределения исходов операций) для конкретного принятого решения, что не позволяет их свести к детерминированным или вероятностным.

Условия оценки эффективности систем для неопределенных операций можно представить в виде таблицы.

Здесь – значение вектора управляемых параметров, определяющий свойства системы ;

– значение вектора неуправляемых параметров, определяющий состояние обстановки;

– значение эффективности значения для состояния обстановки ;

– эффективность системы .

В зависимости от характера неопределенности операции могут делиться на игровые и статистические неопределенные.

В игровых операциях неопределенность вносит своими сознательными действиями противник. Как в этом случае находится оптимальное решение, мы рассматривали в п.7.

Условия статистически неопределенных операций зависят от объективной действительности, называемой природой. В этом случае применяется теория статистических решений.

Единого критерия оценки эффективности для неопределенных операций не существует. Разработаны лишь общие требования к критериям оценки и выбора оптимальных систем. Основными требованиями являются:

1. оптимальное решение не должно меняться с перестановкой строк и столбцов матрицы эффективности;

2. оптимальное решение не должно меняться при добавлении тождественной строки или столбца к матрице эффективности;

3. оптимальное решение не должно меняться от добавления постоянного числа к значению каждого элемента матрицы эффективности;

4. оптимальное решение не должно становиться неоптимальным и, наоборот, в случае добавления новых систем, среди которых нет ни одной более эффективной системы;

5. если система и оптимальны, то вероятностная смесь этих систем тоже должна быть оптимальна.

В зависимости от характера предпочтений ЛПР наиболее часто в неопределенных операциях используются критерии:

а) среднего выигрыша;

б) Лапласа;

в) осторожного наблюдателя (Вальда);

г) максимакса;

д) пессимизма–оптимизма (Гурвица);

е) минимального риска.

Пример: Необходимо оценить один из трех разрабатываемых программных продуктов для борьбы с одним из четырех типов программных воздействий .

Пусть дана матрица эффективности (рис. 14.2)

	0,1	0,5	0,1	0,2
	0,2	0,3	0,2	0,4
	0,1	0,4	0,4	0,3

Рис. 14.2

Здесь – программный продукт – оценка эффективности применения программного продукта при программном воздействии .

а) критерий среднего выигрыша.

Данный критерий предполагает задание вероятностей состояний обстановки . Эффективность систем оценивается как 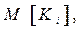т.е.

Оптимальной системы будет соответствовать эффективность

Пусть в нашем случае . Тогда получим следующие оценки систем:

Оптимальное решение – система .

б) критерий Лапласа.

В основе критерия лежит предположение: поскольку о состоянии обстановки ничего не известно, то их можно считать равновероятностными. Исходя из этого:

В нашем случае

Оптимальное решение – система a₃. Критерий Лапласа представляет собой частный случай критерия среднего выигрыша.

в) критерий осторожного наблюдателя (Вальда) – это максиминный критерий, он гарантирует определенный выигрыш при наихудших условиях.

Оптимальной считается система из строки с максимальным значением эффективности:

В нашем случае

Оптимальное решение – система .

Максиминный критерий ориентирует на решение, не содержащее элементов риска; в этом его недостаток, другой – он не удовлетворяет условию 3.

г) критерий максимакса.

Критерий максимакса – самый оптимистический критерий. Те, кто предпочитают им пользоваться, всегда надеются на лучшее состояние обстановки, и естественно, в большей степени рискуют.

В нашем случае

Оптимальное решение – система .

д) критерий пессимизма – оптимизма (Гурвица).

Это критерий обобщенного максимина. Для этого вводится коэффициент оптимизма , характеризующий отношение к риску лица, принимающего решение. Эффективность систем находится как взвешенная с помощью коэффициента 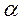сумма максимальной и минимальной оценок:

Условие оптимальности записывается в виде

Пусть и рассчитаем эффективность систем для рассматриваемого примера:

Оптимальное системой будет .

При критерий Гурвица сводится к критерию максимина, при – к критерию максимакса. На практике пользуются значениями коэффициента в пределах 0,3–0,7. В критерии Гурвица не выполняются требования 4 и 5.

е) критерий минимального риска (Сэвиджа).

Этот критерий минимизирует потери при наихудших условиях.

Преобразуем матрицу эффективности в матрицу потерь (риска), в которой элементы определяются соотношением:

И используем критерий минимакса:

Обратимся опять к рассматриваемому примеру. В нем матрице эффективности будет соответствовать матрица потерь:

	0,1		0,3	0,2
		0,2	0,2
	0,1	0,1		0,1

Тогда

О критерии Сэвиджа можно сказать, что в нем по сравнению с критерием Вальда придается несколько большее значение выигрышу, чем проигрышу. Основной недостаток критерия – не выполняется требование 4.

Таким образом, эффективность систем в неопределенных операциях может оцениваться по целому ряду критериев. На выбор того или иного критерия оказывает влияние ряд факторов:

а) природа конкретной операции и ее цель (в одних операциях допустим риск, в других – важен гарантированный результат);

б) причины неопределенности (одно дело, когда неопределенность является случайным результатом действия объективных законов природы, и другое, когда она вызывается действиями разумного противника, стремящегося помешать в достижении цели);

в) характер лица, принимающего решения (одни люди склонны к риску, в надежде добиться большего успеха, другие предпочитают действовать всегда осторожно).

Date: 2016-02-19; view: 2050; Нарушение авторских прав