Частотные характеристики объекта регулирования

С помощью ввода ниже приведённых команд в программе:

n1=[0.2]; d1=[3.3 1];

n2=[1.2]; d2=[1.9 1];

n3=[3.1]; d3=[1.2 1];

[num4,den4]=pade(0.5,1);

[num1,den1]=series(n1,d1,n2,d2);

[num2,den2]=series(num1,den1,n3,d3);

[num3,den3]=series(num2,den2,num4,den4);

nyquist(num3,den3);

grid on

Получается график, называемый годографом Найквиста (рисунок 7).

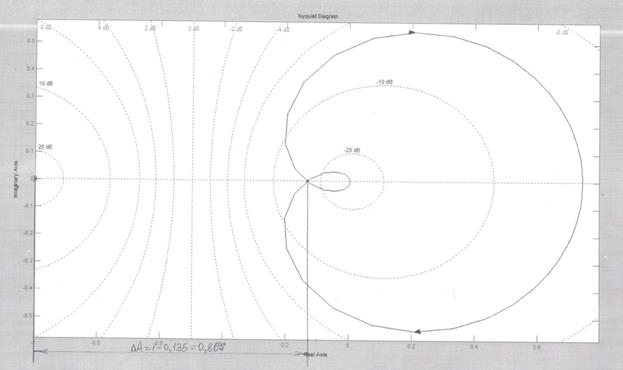
Рисунок 7- Частотная характеристика объекта регулирования

На этом графике видно, что система устойчива, так как не охватывает точку с координатами (-1; j0). И на этом же графике нужно определить запас устойчивости системы =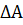

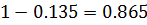
Таким же образом на графике определим запас устойчивости по ЛАФЧХ (рисунок 8).

В программе прописываем следующие команды:

n1=[0.2]; d1=[3.3 1];

n2=[1.2]; d2=[1.9 1];

n3=[3.1]; d3=[1.2 1];

[num4,den4]=pade(0.5,1);

[num1,den1]=series(n1,d1,n2,d2);

[num2,den2]=series(num1,den1,n3,d3);

[num3,den3]=series(num2,den2,num4,den4);

bode(num3,den3);

grid on

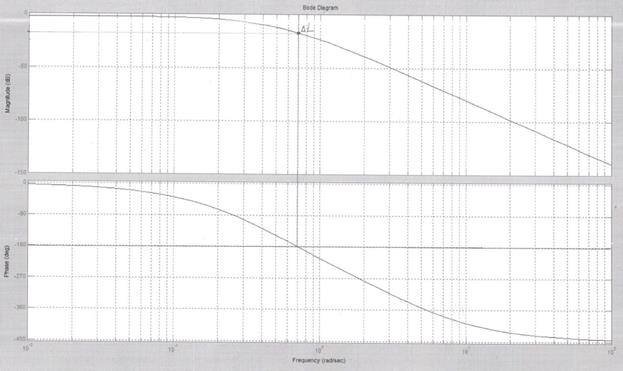
Рисунок 8 – Логарифмическая амплитудно-фазовая частотная характеристика

На графике ЛАФЧХ (рисунок 8) возможно определить запас устойчивости по модулю ( А вот определить запас устойчивости по фазе (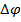) не представляется возможным, так как график начинается ниже 0.

2 Синтез системы автоматического регулирования

Так как предложенный по заданию закон регулирования ПИД, то выпишем уравнение (1) этого закона.

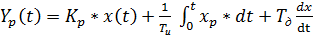(1)

Также у закона регулирования есть передаточная функция (2), отметим её.

(2)

Приведём к общему знаменателю передаточную функцию (2).

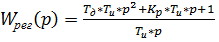(3)

Далее, исходя из передаточной функции (3), нужно записать комплексную частотную передаточную функцию (4). При расчёте следует учитывать, что мнимая единица в квадрате равна минус одному.

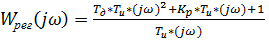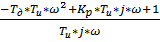= (4)

В получившейся комплексной частотной передаточной функции (4) нужно знаменатель освободить от мнимой единицы, а добьёмся мы этого перемножением дроби на мнимую единицу.

/ ;

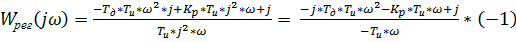(5)

Следующим шагом будет определение действительной и мнимой части комплексной частотной передаточной функции, для этого в формуле (5) в числителе мнимую единицу вынесем за скобку.

(6)

Действительная часть:

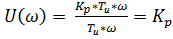(7)

Мнимая часть:

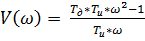(8)

Поскольку действительная и мнимая части определены, их нужно подставить в формулу(9) по нахождению амплитудно-частотной характеристики.

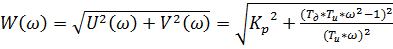(9)

Вслед за этим, 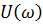и 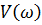подставим в формулу 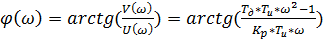(10).

(10)

Таким образом, получается, пять частотных характеристик: комплексная частотная 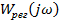, действительную частотную 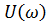, мнимую частотную , амплитудно-частотная ифазочастотную .

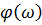Date: 2016-02-19; view: 413; Нарушение авторских прав