
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Нечеткие высказывания
|
|
Определение 4.2. Нечетким высказыванием называется высказывание  , степень истинности которого m(
, степень истинности которого m( ) можно оценить числом из интервала [0, 1], m(
) можно оценить числом из интервала [0, 1], m( ) Î [0, 1]. Если m(
) Î [0, 1]. Если m( ) = 0,5, то высказывание называется индиффирентным.
) = 0,5, то высказывание называется индиффирентным.
Определение 4.3. Нечеткой высказывательной переменной  называется нечеткое высказывапние
называется нечеткое высказывапние  , степень истинности которого может меняться в интервале [0, 1].
, степень истинности которого может меняться в интервале [0, 1].
Так как степень истинности нечеткого высказывания не связана с сутью высказывания, будем в дальнейшем отождествлять нечеткое высказывание с его степенью истинности аналогично тому, как обычное четкое высказывание отождествлялось с его истинностью или ложностью (см. п. 1. 1). Нечеткие высказывания и степень их истинности будем обозначать большими буквами с тильдой::  ,
,  ,
,  , и т. д.
, и т. д.
На множестве нечетких высказываний вводятся логические операции, аналогичные операциям алгебры высказываний.
1. Отрицание нечеткого высказывания:
Ø  = 1 –
= 1 –  . (4.1)
. (4.1)
2. Конъюнкция нечетких высказываний:
 &
&  = min (
= min ( ,
,  ). (4.2)
). (4.2)
3. Дизъюнкция нечетких высказываний:
 Ú
Ú  = max (
= max ( ,
,  ). (4.3)
). (4.3)
4. Импликация нечетких высказываний:
 É
É  = max (1 –
= max (1 –  ,
,  ). (4.4)
). (4.4)
5. Эквивалентность нечетких высказываний:
 ~
~  = min (max (1 –
= min (max (1 –  ,
,  ), max (
), max ( , 1 –
, 1 –  )). (4.5)
)). (4.5)
Старшинство операций принято в поядке1) – 5).
Пример 4.5.
Найти степень истинности высказывания
 = (
= ( Ú
Ú  ) ~ (
) ~ ( É (
É ( &
&  )) при
)) при  = 0,8;
= 0,8;  = 0,3.
= 0,3.
Порядок действий определяется старшинством операций и скобками.
1.  &
&  = min (0,8; 0,3) = 0,3.
= min (0,8; 0,3) = 0,3.
2. ( É (
É ( &
&  ) = max (1 – 0,8; 0,3) = 0,3.
) = max (1 – 0,8; 0,3) = 0,3.
3.  Ú
Ú  = max (0,8; 0,3) = 0,8.
= max (0,8; 0,3) = 0,8.
4.  = min (max (1 – 0,8; 0,3), max (0,8; 1 – 0,3)) = min (0,3; 0,8) = 0,3.
= min (max (1 – 0,8; 0,3), max (0,8; 1 – 0,3)) = min (0,3; 0,8) = 0,3.
Множество нечетких высказываний вместе с введенными на них операциями образуют алгебру нечетких высказываний.
Определение 4.4. Нечеткой логической формулой называется:
а) любая нечеткая высказывательная переменная;
б) если  и
и  – нечеткие логические формулы, то Ø
– нечеткие логические формулы, то Ø  ,
,  &
&  ,
,  Ú
Ú  ,
,  É
É  ,
,  ~
~  – тоже нечеткие логические формулы.
– тоже нечеткие логические формулы.
Определение 4.5. Пусть  (
( 1,
1,  2, …,
2, …,  n) и
n) и  (
( 1,
1,  2, …,
2, …,  n) – две нечеткие логические формулы. Степенью равносильности формул
n) – две нечеткие логические формулы. Степенью равносильности формул  и
и  называется величина
называется величина
m( ,
,  ) =
) =  {
{  (a1, a2, …,a n) ~
(a1, a2, …,a n) ~  (a1, a2, …,a n)} (4.6)
(a1, a2, …,a n)} (4.6)
Здесь логические операции конъюнкции и эквивалентности имеют смысл, определенный выше для логических операций над нечеткими высказываниями, причем конъюнкция берется по всем наборам степеней истинности (a1, a2, …,a n) нечетких переменных ( 1,
1,  2, …,
2, …,  n).
n).
Множество всех наборов степеней истинности (a1, a2, …,a n) нечетких переменных ( 1,
1,  2, …,
2, …,  n) назовем полной областью определения Cn. Очевидно, что множество Cn имеет мощность континнуума в отличие от двузначной логики высказываний, где число всех наборов переменнх конечно и равно 2 n.
n) назовем полной областью определения Cn. Очевидно, что множество Cn имеет мощность континнуума в отличие от двузначной логики высказываний, где число всех наборов переменнх конечно и равно 2 n.
Если m( ,
,  ) = 0,5, то нечеткие формулы
) = 0,5, то нечеткие формулы  и
и  называются индиффирентными.
называются индиффирентными.
Если m( ,
,  ) > 0,5, то нечеткие формулы
) > 0,5, то нечеткие формулы  и
и  называются нечетко равносильными.
называются нечетко равносильными.
Если m( ,
,  ) < 0,5, то нечеткие формулы
) < 0,5, то нечеткие формулы  и
и  называются нечетко неравносильными..
называются нечетко неравносильными..
Определение 4.6. Степенью неравносильности формул  и
и  называется величина
называется величина
 (
( ,
,  ) = 1 – m(
) = 1 – m( ,
,  ).
).
Пример 4.6
Определить степень равносильности формул.
 =
=  É
É 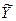 ,
,  = Ø(
= Ø( &
& 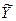 ) при условии, что
) при условии, что  и
и 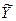 прнимают значения степеней истинности из множества {0,1; 0,2}. Перечислим все возможные наборы значений
прнимают значения степеней истинности из множества {0,1; 0,2}. Перечислим все возможные наборы значений  и
и 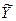 :
:
A 1 = {0,1; 0,1}; A 2 = {0,1; 0,2}; A 3 = {0,2; 0,1}; A 4 = {0,2; 0,2}.
Запишем формулы  и
и  с учетом (4.1), (4.2), (4.4):
с учетом (4.1), (4.2), (4.4):
 =
=  É
É 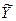 = max (1 –
= max (1 –  ,
, 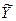 );
);  = Ø(
= Ø( &
& 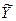 ) = 1 –
) = 1 –  &
& 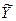 = 1 – min (
= 1 – min ( ,
, 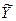 ).
).
Вычислим формулы  и
и  на каждом из четырех наборов A 1 – A 4:
на каждом из четырех наборов A 1 – A 4:
 1 = max (1 – 0,1; 0.1) = 0,9.
1 = max (1 – 0,1; 0.1) = 0,9.
 2 = max (1 – 0,1; 0,2) = 0,9.
2 = max (1 – 0,1; 0,2) = 0,9.
 3 = max (1 – 0,2; 0,1) = 0,8.
3 = max (1 – 0,2; 0,1) = 0,8.
 4 = max (1 – 0,2; 0,2) = 0,8.
4 = max (1 – 0,2; 0,2) = 0,8.
 1 = 1 – min (0,1; 0.1) = 0,9.
1 = 1 – min (0,1; 0.1) = 0,9.
 2 = 1 – min (0,1; 0,2) = 0,9.
2 = 1 – min (0,1; 0,2) = 0,9.
 3 = 1 – min (0,2; 0,1) = 0,9.
3 = 1 – min (0,2; 0,1) = 0,9.
 4 = 1 – min (0,2; 0,2) = 0,8.
4 = 1 – min (0,2; 0,2) = 0,8.
Вычислим теперь степень равносильности формул  и
и  в соответствии с (4.6):
в соответствии с (4.6):
Для этого сначала вычислим  (a1, a2, …,a n) ~
(a1, a2, …,a n) ~  (a1, a2, …,a n)} для всех наборов A 1 – A 4:
(a1, a2, …,a n)} для всех наборов A 1 – A 4:
В соответствии с (4.5) имеем
 ~
~  = min (max (1 –
= min (max (1 –  ,
,  ), max (
), max ( , 1 –
, 1 –  )).
)).
Поэтому
 1 ~
1 ~  1 = min (max (1 – 0,9;0,9), max (0,9; 1 –0,9)) = 0,9.
1 = min (max (1 – 0,9;0,9), max (0,9; 1 –0,9)) = 0,9.
 2 ~
2 ~  2 = min (max (1 – 0,9;0,9), max (0,9; 1 –0,9)) = 0,9.
2 = min (max (1 – 0,9;0,9), max (0,9; 1 –0,9)) = 0,9.
 3 ~
3 ~  3 = min (max (1 – 0,8;0,9), max (0,8; 1 –0,9)) = 0,8.
3 = min (max (1 – 0,8;0,9), max (0,8; 1 –0,9)) = 0,8.
 4 ~
4 ~  4 = min (max (1 – 0,8;0,8), max (0,8; 1 –0,8)) = 0,8.
4 = min (max (1 – 0,8;0,8), max (0,8; 1 –0,8)) = 0,8.
Окончательно по (4.6) получим
m( ,
,  ) =
) =  {
{  (a1, a2, …,a n) ~
(a1, a2, …,a n) ~  (a1, a2, …,a n)} = 0,9&0,9&0,8&0,8 = min (0,9; 0,9; 0,8; 0,8) = 0,8.
(a1, a2, …,a n)} = 0,9&0,9&0,8&0,8 = min (0,9; 0,9; 0,8; 0,8) = 0,8.
Формулы  и
и  нечетко равносильны.
нечетко равносильны.
На других наборах степеней истинности нечетких переменных  и
и 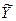 формулы
формулы  и
и  могут быть нечетко неравносильны.
могут быть нечетко неравносильны.
Определение 4.7. Пусть  (
( 1,
1,  2, …,
2, …,  n) и
n) и  (
( 1,
1,  2, …,
2, …,  n) – две нечеткие логические формулы, рассмотренные на некотором множестве M изменения нечетких переменных
n) – две нечеткие логические формулы, рассмотренные на некотором множестве M изменения нечетких переменных  1,
1,  2, …,
2, …,  n. Областью нечеткой равносильности формул
n. Областью нечеткой равносильности формул  и
и  называется подмножество множества M, на котором формулы
называется подмножество множества M, на котором формулы  и
и  нечетко равносильны.
нечетко равносильны.
Пример 4.7.
Вернемся к примеру 4.7. Для этого примера множество M состоит из девяти наборов:
M = {{0,1; 0,1}; {0,1; 0,2}; {0,2; 0,1}; {0,2; 0,2}}.
На каждом наборе формулы  и
и  нечетко равносильны, так как m(
нечетко равносильны, так как m( ,
,  ) > 0,5. Поэтому областью нечеткой равносильности будет все множество M.
) > 0,5. Поэтому областью нечеткой равносильности будет все множество M.
Определение 4.8. Если формула  (
( 1,
1,  2, …,
2, …,  n) на всех наборах переменных
n) на всех наборах переменных  1,
1,  2, …,
2, …,  n из некоторого множества M имеет степень истинности большую или равную 0,5, то она будет на нем нечетко истинной. Обозначается это так:
n из некоторого множества M имеет степень истинности большую или равную 0,5, то она будет на нем нечетко истинной. Обозначается это так:  =
=  .
.
Определение 4.9. Если формула  (
( 1,
1,  2, …,
2, …,  n) на всех наборах переменных
n) на всех наборах переменных  1,
1,  2, …,
2, …,  n из некоторого множества M имеет степень истинности меньшую или равную 0,5, то она будет на нем нечетко ложной. Обозначается это так:
n из некоторого множества M имеет степень истинности меньшую или равную 0,5, то она будет на нем нечетко ложной. Обозначается это так:  =
=  .
.
Пример 4.8.
Покажем, что  Ú Ø
Ú Ø  =
=  и
и  & Ø
& Ø  =
=  для всех значений нечеткой переменной
для всех значений нечеткой переменной  :
:
0 £  £ 1.
£ 1.
Учитывая (4,1), (4.2), (4. 3), имеем
 Ú Ø
Ú Ø  = max (
= max ( , Ø
, Ø  ) = max (
) = max ( , 1 –
, 1 –  ) ³ 0,5.
) ³ 0,5.
 & Ø
& Ø  = min (
= min ( , Ø
, Ø  ) = min (
) = min ( , 1 –
, 1 –  ) £ 0,5.
) £ 0,5.
Date: 2016-01-20; view: 1150; Нарушение авторских прав