
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Частота встречаемости зарубежных/отечественных фильмов на сайте megogo. Net
|
|
1.1 Теоретическое описание фильмов сайта megogo.net
После тяжелого дня некоторые люди хотят расслабиться за чашечкой теплого чая и просмотром хорошего интересного фильма, на который можно потратить основную часть своего отдыха. Выбор фильма — важен, для того что бы получить волну впечатлений. Наша выборка будет сделана из сайта megogo.net.MEGOGO — Украинская меди компания, предоставляющая услуги онлайн-кинотеатра на просторах сайта megogo.net можно найти огромное количество фильмов разных жанров. Как и на любом сайте интернета посвящённому онлайн просмотру фильмов, здесь можно встретить самые различные жанры и категории фильмов. Но среди всего многообразия фильмов, все фильмы можно условно разделить на две группы, в зависимости от страны в которой был снят фильм. - «отечественные» и «зарубежные». Под «отечественными» понимаются фильмы, снятые в Казахстане в таких киностудиях как «Телекомпания Калиот», «Кинокомпания Евразия фильм», «Life production» и т.д.. «зарубежные же» же – фильмы, производимые в других странах, таких как, Япония, Германия, Америка и т.п. Если просмотреть сайт megogo.net, то нетрудно заметить, что одни фильмы встречаются чаще других, то есть одни фильмы более популярны, чем другие. И такой фактор, как популярность фильма занимает не последнее место в выборе просматриваемого фильма зрителем. При выборе фильма важно учитывать популярность фильма, так как просмотр популярного фильма дает уверенность будет впечатляющим и запомнится своим сюжетом. Зайдя на сайт можно выбрать нужную вам категорию жанра, согласно которому и будет совершаться выбор в просмотре фильма.
1.2 Популярность «отечественных» фильмов
Для определения популярности фильмов необходимо определить, какие фильмы встречаются чаще. Зайдя на просторы интернета был выбран первый сайт, предоставляющий услуги онлайн просмотра фильмов. Выбор пал на украинскую медиа-компанию Megogo, база зрителей которой постоянно растет.
На сайте megogo.net, случайным образом было проверено 50 фильмов, которые распределились, как показано в таблице 1.1, в зависимости от страны производителя следующим образом:
Таблица 1.1
Распределение фильмов по странам
| Группа | Отечественные | Зарубежные | Итого |
| Количество |
Можно ли на основании полученных данных сказать, что все фильмы
пользуются одинаковой популярностью?
В данном случае имеется одна выборка и необходимость проверить, соответствует ли распределение результатов в выборке предполагаемому распределению.
Так как в данном случае у нас имеется небольшая выборка, используется непараметрический тест. Для решения подобных задач применяется один из наиболее популярных непараметрических тестов — тест  .
.
В качестве теоретического распределения в нашем случае используется равномерное распределение. Смысл его в том, что все результаты считаются равновероятными. При наличии двух групп фильмов вероятность встретить фильм, принадлежащую какой-либо из них, должна быть одна и та же и равна 1/2=0,5.
С учетом данного обстоятельства окончательный вариант
расчетной таблицы для данного примера представлен в таблице 1.2.
Таблица 1.2
Теоретическое и эмпирическое распределение фильмов
| Группа | Отечественные | Зарубежные | Итого |
| Теоретическое количество | |||
| Эмпирическое количество |
Формулируем нулевую и альтернативную гипотезы и задаем уровень значимости 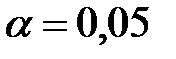 .
.
Н0: Вероятность встретить на сайте megogo.net фильм отечественного производства, равна вероятности встретить фильм, произведенный в зарубежных странах (Если 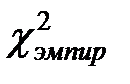 меньше
меньше 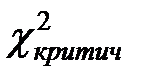 ).
).
Н1: Вероятность встретить на сайте megogo.net фильм отечественного производства, не равна вероятности встретить фильм, произведенный в зарубежных странах (Если 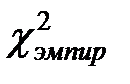 больше или равно
больше или равно 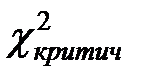 ).
).
Вычисляем сумму отклонений между наблюдаемыми и
теоретическими значениями по формуле:
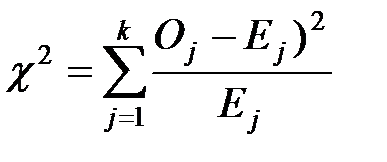 ,
,
где 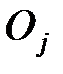 — наблюдаемые, или эмпирические, значения (частоты) для
— наблюдаемые, или эмпирические, значения (частоты) для
каждой из категорий, 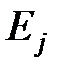 — ожидаемые, или теоретические, значения (частоты) для каждой из категорий таблицы
— ожидаемые, или теоретические, значения (частоты) для каждой из категорий таблицы
Подставим соответствующие значения  и
и 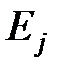 в расчетную формулу:
в расчетную формулу:

Таблица 1.3
Распределение теоретических и эмпирических частот
| Категории | |||
| итого | |||
| Ожидаемые и эмпирические частоты | 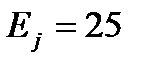 , , 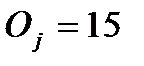
| 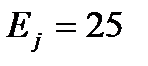 , , 
|
Полученное значение 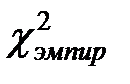 сравнивается со значением
сравнивается со значением 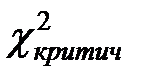 , которое берется из таблицы критических значений для теста
, которое берется из таблицы критических значений для теста 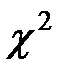 (см. Приложение Таблица 1)в зависимости от выбранного уровня значимости
(см. Приложение Таблица 1)в зависимости от выбранного уровня значимости 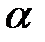 и числа степеней свободы. В свою очередь, число степеней свободы для теста
и числа степеней свободы. В свою очередь, число степеней свободы для теста 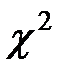 зависит от размера расчетной таблицы и равно
зависит от размера расчетной таблицы и равно 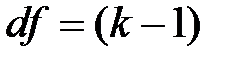 . В нашем случае
. В нашем случае 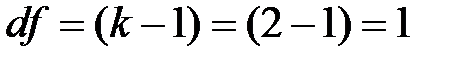 .
.
Если 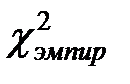 больше или равно
больше или равно 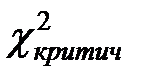 , то нулевая гипотеза отклоняется и принимается альтернативная (эмпирическое распределение значимо отличается от теоретического: фильмы одних стран-производителей встречаются на просторах сайта megogo.net чаще или реже, чем фильмы других).
, то нулевая гипотеза отклоняется и принимается альтернативная (эмпирическое распределение значимо отличается от теоретического: фильмы одних стран-производителей встречаются на просторах сайта megogo.net чаще или реже, чем фильмы других).
Из таблицы 1 находим, что для 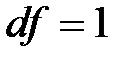 и
и 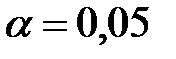 ,
, 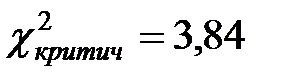 .
.
Поскольку 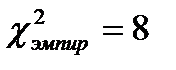 гораздо больше, чем
гораздо больше, чем  , то нулевая гипотеза отклоняется и принимается альтернативная. То есть, Вероятность встретить на сайте megogo.net фильм отечественного производства, не равна вероятности встретить фильм, произведенный в зарубежных странах.
, то нулевая гипотеза отклоняется и принимается альтернативная. То есть, Вероятность встретить на сайте megogo.net фильм отечественного производства, не равна вероятности встретить фильм, произведенный в зарубежных странах.
Для определения популярности «отечественных» фильмов можно воспользоваться и параметрическими методами. Для этого необходимо собрать несколько больше статистических данных.
Для исследования были собраны данные из 100 выборок, в каждой из которых рассматривалось по 20 фильмов. Статистические данные представлены в таблице 1.4.
Таблица 1.4
Статистические данные фильмов из 100 выборок
| Номер выборки | Число отечественных фильмов | Номер выборки | Число отечественных фильмов | Номер выборки | Число отечественных фильмов | Номер выборки | Число отечественных фильмов |
Так как параметрические методы применяются при нормальном распределении, проверим, наши данные на нормальность.
Для того чтобы распределение было нормальным, нужно чтобы среднее, мода и медиана были равны.
Модой (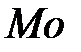 ) называется наиболее часто встречающееся значение среди имеющихся. Для того чтобы разобраться с модой, построим дополнительную таблицу. Поместим в нее значения встречающихся «отечественных» фильмов от минимального количества(1) до максимального (5), и укажем, сколько раз встречается то или иное количество фильмов (табл. 1.5).
) называется наиболее часто встречающееся значение среди имеющихся. Для того чтобы разобраться с модой, построим дополнительную таблицу. Поместим в нее значения встречающихся «отечественных» фильмов от минимального количества(1) до максимального (5), и укажем, сколько раз встречается то или иное количество фильмов (табл. 1.5).
Таблица 1.5
Частота встречаемости «отечественных» фильмов
| Число отечественных фильмов | |||||
| Частота |
Как видно из таблицы, чаще всего на каждые 20 фильмов встречается 3 «отечественных» (это значение встречается чаще всего — 40 раз). Поэтому мода появления «отечественных» фильмов равна—3.
Новая таблица содержит ту же самую информацию, что и предыдущая, но она заметно короче, данные в ней упорядочены по возрастанию, и с ней удобней работать.
Медиана (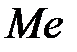 ) представляет собой значение, которое делит упорядоченные данные пополам таким образом, что одна половина данных оказывается меньше медианы, а другая — больше.
) представляет собой значение, которое делит упорядоченные данные пополам таким образом, что одна половина данных оказывается меньше медианы, а другая — больше.
Нахождение медианы не носит столь наглядного характера, как нахождение моды. Для определения медианы приходится прибегать к дополнительным преобразованиям и вычислениям. Во-первых, дополним таблицу еще двумя строками и получим таблицу 1.6.
Таблица 1.6
Частота, накопленная частота и процент встречаемости фильмов
| Число отечественных фильмов | |||||
| Частота | |||||
| Накопленная частота | |||||
| % |
В первой из дополнительных строк запишем значения так называемых «накопленных» (или кумулятивных) частот, которое будет равно 100.
Во-вторых, запишем в следующую графу, какой процент от 100
составляет каждое значение накопленных частот. В нашем случае значения третей и четвертой строк совпадают, так как частота равняется 100. Вообще могут получаться не одинаковые значения.
Попытаемся понять смысл полученного в последней графе результата.
При переходе от столбца со значением числа фильмов «2» к столбцу со значением «3» за плечами остается 35% всех результатов. А при переходе от столбца со значением «3» к столбцу «4» за плечами уже 75%. Медиана — это та точка, которая делит все данные в отношении 50:50. Очевидно, требуемая точка где-то внутри столбца со значением «3». То есть 
Для нахождения среднего используется простая формула, смысл которой в том, чтобы сложить все значения(в нашем случае значения количества встреченных «отечественных» фильмов) и разделить полученный результат на число значений (в нашем случае 100).
Дальше можно идти двумя путями.
Во-первых, начать непосредственно складывать все 100 значений из первой таблицы.
Во-вторых, догадаться, что если некоторые значения количества просмотренных фильмов встречаются несколько раз, то можно воспользоваться данными из таблицы 1.2 и перейти от сложения повторяющихся значений к умножению этих значений на число повторов(например, число машин 1 встречается в первой таблице 10 раз, значит вместо 1 + 1 + 1 + 1+1+1+1+1+1 можно записать 1x10). Тогда:
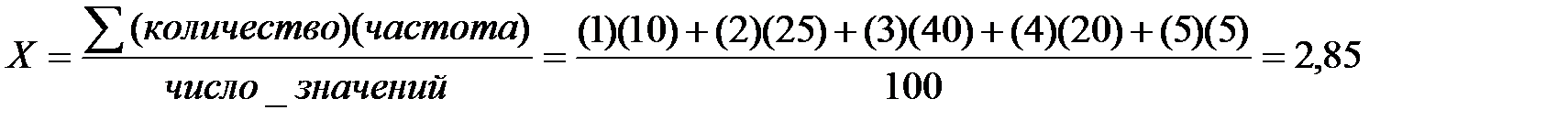
Среднее значение получилось близким к трем.
Исходя их найденных значений моды, медианы и среднего, можно утверждать, что данное распределение можно считать нормальным, так как значения моды и медианы абсолютно равны, а значение среднего отличается на 0,15. Если взять большее количество испытаний, то среднее значение будет приближаться к трем.
На диаграмме 1, можно просмотреть, что закон распределения стремится к нормальному.
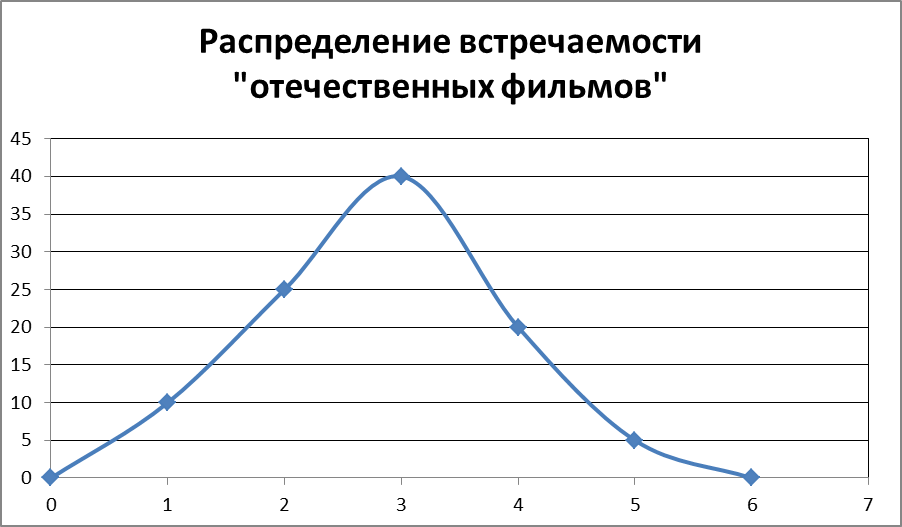
Диаграмма 1.
Теперь приступим к проверке гипотезы.
Н0: Вероятность встретить на сайте megogo.net фильм отечественного производства, равна вероятности встретить фильм, произведенный в зарубежных странах.
Н1: Вероятность встретить на сайте megogo.net фильм отечественного производства, не равна вероятности встретить фильм, произведенный в зарубежных странах.
Наш прогноз 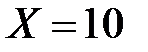 , выборка
, выборка 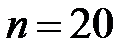 , средняя
, средняя  .
.
Меры центральной тенденции показывают, вокруг каких значений
группируется большинство экспериментальных данных. Обычно в качестве «центра» такого группирования рассматривается среднее (X).
Меры изменчивости говорят о том, в какой степени полученные результаты отклоняются от «центра группирования», что чаще всего приводит к определению меры отклонения экспериментальных данных от среднего. В принципе, в качестве меры изменчивости можно было бы использовать среднее значение отклонений текущих значений от среднего. Для этого необходимо определить, насколько каждое значение количества фильмов отклоняется в большую или меньшую сторону от X—2,895 затем сложить все результаты и разделить на число значений. К сожалению, этот путь невозможен, поскольку, как правило, отклонения от среднего в большую сторону (со знаком «+») и в меньшую сторону (со знаком «—») компенсируют друг друга и в сумме дают ноль. Для решения этой проблемы лучше использовать не отклонение от среднего, а квадрат этого отклонения, потому что такая процедура позволяет избавиться от влияния знака. Вначале делается та же операция — определяется, насколько каждое значение возраста отклоняется в большую или меньшую сторону от Х= 2,85. Затем каждый из полученных результатов возводится в квадрат, все складывается и делится на число значений. Получаемая таким образом мера изменчивости называется дисперсией. Данные приведены в таблице 1.7.
Таблица 1.7
Вычисление дисперсии
| Число фильмов | Частота | (Число фильмов-Среднее) | (Число фильмов - Среднее)2 | (Частота)*(фильмов - Среднее)2 |
| -1,85 | 3,42 | 34,2 | ||
| -0,85 | 0,72 | |||
| 0,15 | 0,02 | 0,8 | ||
| 1,15 | 1,32 | 26,4 | ||
| 2,15 | 4,62 | 23,1 |
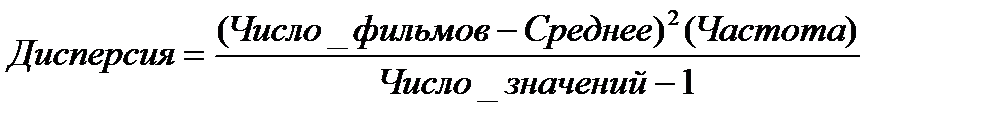 .
.
Подставим в эту формулу необходимые значения из таблицы

К сожалению, дисперсия оказывается не очень удобным показателем меры изменчивости.
Для решения возникшей проблемы вместо значения дисперсии используется квадратный корень из нее. Полученное таким образом новое значение называется стандартным отклонением и является наиболее популярной мерой изменчивости. Стандартное отклонение часто обозначается как 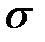 (сигма):
(сигма):

Для нашего случая:
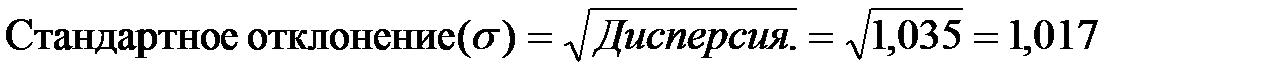 .
.
Проверим гипотезу по формуле Стьюдента 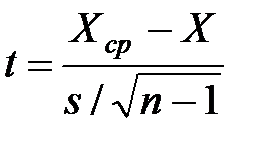 .
.
Выбирается уровень значимости a и критическая область А, так, чтобы условная вероятность попадания критерия в А при условии справедливости гипотезы 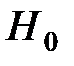 равнялась a.
равнялась a.
Выберем a=0.05 (вероятность не принять верный прогноз). По табл. распределения Стьюдента находим критическое значение (квантиль) (см. Приложение Таблица2) 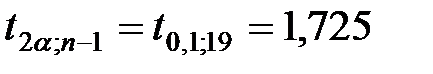
критерия
Þ Р{|t|>1,725}=0.05,
Þ критическая область А:
|t|>1,725.


То есть прогноз должен быть отвергнут, так как отклонение от него в сторону повышения не является случайностью.
Гипотеза о том, что прогноз верен, проверена по критерию 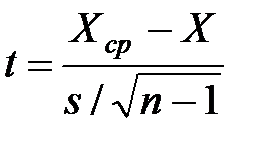 на уровне значимости 5% и отвергнута.
на уровне значимости 5% и отвергнута.
Date: 2016-01-20; view: 480; Нарушение авторских прав