Доказать или опровергнуть теорему, формализованную в результате выполнения задания 1, используя метод резолюций логики высказываний

6. Формализовать высказывание логики предикатов:

6.1) Предположим, что последовательности {Xn} и {Yn} сходятся, при этом, при n®¥: lim(x_n)=x, lim(y_n)=y. Тогда сходятся и последовательности {Xn+Yn},{Xn-Yn},{Xn*Yn},{Xn/Yn};

6.2) Если |x_n|<y_n при всех n>N₀ и если ряд Sy_n сходится, то сходится и ряд Sx_n;

6.3) Пусть, задан ряд Sx_n. Пусть, при n®¥: a=lim|x_n|^1/n. Ряд сходится при a<1 и расходится при a>1. При a=1 ряд может как сходиться, так и расходиться;

6.4) Пусть, функция f(x) задана на множестве X, имеющем точку a своей предельной точкой. Тогда для того чтобы существовал предел функции f(x) при x® a, необходимо и достаточно, чтобы для любого e>0 нашлось s=s(e) такое, что при любых x, x`ÎX, удовлетворяющих требованиям 0£|x- a |<s(e), 0<|x`- a |<s(e), выполнялось неравенство |f(x)-f(x`)|<e;

6.5) Функция f(x) имеет в точке x= a предел тогда и только тогда, когда она имеет в этой точке левый и правый пределы и эти пределы совпадают;

6.6) Если функция f(x) задана в окрестности точки x=x₀ и непрерывна в точке x=x₀, то существует окрестность |x-x₀|<s этой точки, в которой функция f(x) ограничена;

6.7) Пусть, функция f(x) непрерывна в точке x=x₀, а функция j(t) непрерывна в точке t=t₀=f(x₀). Тогда сложная функция y=j(f(x)) непрерывна в точке x=x₀;

6.8) Любые две первообразные f1(x) и f2(x) для функции g(x) на интервале (a,b) отличаются друг от друга на постоянную, т.е. f1(x) –f2(x) = const;

6.9) Первообразные f1(x) и f2(x) для функции g(x) совпадают на интервале (a,b), если они совпадают хотя бы в одной точке xÎ(a,b);

6.10) Пусть, функция y=f(x) определена на отрезке [a,b] и имеет в точке сÎ(a,b) производную f’(c)¹0. Тогда, если f’(c)>0, то функция f(x) возрастает в точке x=c; если же f’(c)<0, то функция f(x) убывает в точке x=c;

6.11) Если функция g(x) имеет на [a,b] конечное число точек разрыва и ограничена на [a,b], то она интегрируема на [a,b]. В частности, интегрируемы кусочно-непрерывные на [a,b] функции f(x);

6.12) Если функция f(x) не ограничена на множестве X и X замкнуто и ограничено, то f(x) не является непрерывной на X;

6.13) Пусть функция F(x,y,z) задана в цилиндрической области и в каждой точке области (x₀,y₀) функция h(z)=F(x₀,y₀,z) – строго монотонная функция переменного z. Тогда уравнение F(x,y,z)=0 определяет в области не более чем одну неявную функцию z=u(x,y);

6.14) Если ряд Sa_k сходится абсолютно, то и любой ряд Sa’_k, полученный перестановкой его членов, также сходится абсолютно и имеет ту же самую сумму;

6.15) Пусть, ряды Sa_k и Sb_k сходятся соответственно к A и B и один из них сходится абсолютно. Тогда ряд Sc_k, являющийся их произведением, сходится к С и при этом с=А*B;

6.16) Если a>b, то найдется такое действительное число с, что a>b+c. Кроме того, найдется такое действительное число d, что a=b+d, и d>c;

6.17) Функция f(x) дифференцируема в точке x=x₀ если она непрерывна в некоторой окрестности точки x₀, т.е. в окрестности точки х₀ limDy=0, при Dх®0;

6.18) Любые два потенциала f1(x) и f2(x) для g(x) отличаются друг от друга в связной области X на постоянную, т.е. f1(x) – f2(x) = const;

6.19) Пусть функции f(x) и g(x) – эквивалентные функции в окрестности точки x=x₀. Тогда, если существует предел limf(x)*h(x)=a, при x®x₀, то существует и предел limg(x)*h(x)=a;

6.20) Первообразные f1(x) и f2(x) для g(x) совпадают на интервале (a,b), если они совпадают хотя бы в одной точке xÎ(a,b);

6.21) Пусть, G – исчисление на основе G1 и D – замкнутая формула в алфавите G, такая, что ее отрицание не является в G теоремой. Тогда простое расширение G с помощью D непротиворечиво;

6.22) Если Р0– тривиальное ограничение П и Р – простое расширение Р0 с помощью множества замкнутых формул В (иначе говоря – Р есть исчисление на основе П, заданное системой аксиом В), то всякая интерпретация множества формул исчисления Р, в которой истинны все формулы из В является моделью для Р;

6.23) Если две формулы, образованные из элементарных предложений с помощью операций конъюнкции, дизъюнкции и отрицания, равносильны, то двойственные им формулы также равносильны;

6.24) Для любых двух эквивалентных формул F₁ и F₂ существует эквивалентное преобразование F₁ в F₂ с помощью простейших эквивалентных преобразований;

6.25) Если в формуле, представляющей функцию, все знаки функций заменить двойственными функциями, то полученная формула, будет описывать функцию, двойственную исходной функции;

6.26) Формула B есть логическое следствие формул A₁, A₂ тогда и только тогда, когда общезначима формула: A₁A₂ÉB;

6.27) Если f₁ (x) и f₂ (y) вычислимы по Тьюрингу, то их композиция g (x)= f₂ (f₁ (x)), так же вычислима по Тьюрингу;

6.28) Не существует алгоритма, позволяющего для любой МТ узнать: применима ли она к конкретному слову в ее внешнем алфавите;

6.29) Ни для какого нетривиального свойства МТ не существует алгоритма, позволяющего распознавать данное свойство у любой МТ;

6.30) Пусть, xÎ(a,b), a=f(a), b=f(b)¹a. Пусть, число g заключено между a и b т.е. (a-g)(b-g)<0. Тогда найдется хотя бы одна точка cÎ(a,b) такая, что f(c)=g.

7. Привести формулу логики предикатов в сколемовскую нормальную форму:

7.1) ;

7.2) ;

7.3) ;

7.4) ;

7.5) ;

7.6) ;

7.7) ;

7.8) ;

7.9) ;

7.10) ;

7.11) ;

7.12) ;

7.13) ;

7.14) ;

7.15) ;

7.16) ;

7.17) ;

7.18) ;

7.19) ;

7.20) ;

7.21) ;

7.22) ;

7.23) ;

7.24) ;

7.25) ;

7.26) ;

7.27) ;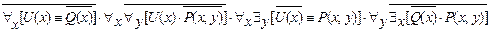

7.28) ;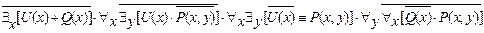

7.29) ;

7.30) .

Date: 2016-01-20; view: 780; Нарушение авторских прав