
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Движущая сила массообменных процессов
|
|
Движущей силой массообменных процессов является разность между рабочей и равновесной концентрациями или наоборот. Это зависит от того, которая из указанных концентраций больше.
На рис. 1.4 приведены возможные варианты выражения движущей силы массообменного процесса при одном и том же направлении перехода распределяемого вещества.
При этом движущую силу можно выражать либо через концентрации распределяемого вещества в фазе G, либо L. В этой связи уравнения массопередачи, записанные по фазам, имеют вид
 ,
,
 . (1.7)
. (1.7)
Индексы у коэффициента скорости процесса  показывают, какие концентрации приняты для выражения движущей силы. В общем случае
показывают, какие концентрации приняты для выражения движущей силы. В общем случае  и
и 

 , но всегда выполняется равенство
, но всегда выполняется равенство
 . (1.8)
. (1.8)
На рис. 1.4. показано, как движущая сила меняется с изменением рабочих концентраций. В этой связи для всего процесса массообмена, протекающего в пределах изменения концентраций от начальных до конечных, должна быть определена средняя движущая сила по газовой фазе  или жидкой –
или жидкой –  .
.




а) б)
Рис. 1.4. Движущая сила массообменного процесса для участка аппарата:
а) по газовой фазе; б) по жидкой фазе
С учетом средней движущей силы процесса основное уравнение массопередачи для всей поверхности контакта фаз может быть записано в виде
 , (1.9)
, (1.9)
 . (1.10)
. (1.10)
При определении движущей силы возможны два случая:
– зависимость между равновесными концентрациями не линейна и определяется функциональной зависимостью самого общего вида типа  ;
;
– зависимость между равновесными концентрациями линейная – 
( – представляет собой постоянную величину).
– представляет собой постоянную величину).
Определим среднюю движущую силу по фазе G для случая перехода распределяемого компонента из газовой в жидкую фазу. Для элемента поверхности имеем
 ;
;  .
.
Из сопоставления предыдущих равенств получим


для элементарной поверхности фазового контакта имеем
 .
.
После интегрирования в пределах 0 – F и  получим
получим
 . (1.11)
. (1.11)
Изменим границы интегрирования с целью исключения отрицательного знака перед интегралом и вставим равенство для  :
:
 . (1.12)
. (1.12)
При выражении движущей силы для жидкой фазы получим аналогичное выражение:
 . (1.13)
. (1.13)
При сравнении уравнений (1.9) и (1.10) с уравнениями (1.12) и (1.13) составим выражения для средних движущих сил по газовой и жидкой фазам:
 , (1.14)
, (1.14)
 . (1.15)
. (1.15)
Интегралы, стоящие в правой части равенств (1.14) и (1.15), называют числами единиц переноса – сокращенно ЧЕП.
Отсюда выражение для ЧЕП в газовой фазе имеет
 ,
,
а выражение для ЧЕП в жидкой фазе:
 .
.
Число единиц переноса, как следует из уравнений (1.14) и (1.15), можно определять по средней движущей силе процесса:
 ,
,
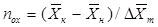 .
.
Физический смысл ЧЕП состоит в том, что эта величина характеризует изменение рабочей концентрации фазы, приходящееся на единицу движущей силы.
Эти соотношения справедливы для всех случаев, когда между рабочими и равновесными концентрациями имеют место линейные и нелинейные зависимости.
Числа единиц переноса выражаются интегралами, которые не могут быть решены аналитически, так как вид функции  или
или  в каждом конкретном случае различен. В связи с этим число единиц переноса
в каждом конкретном случае различен. В связи с этим число единиц переноса  и
и  определяют методом графического или численного интегрирования.
определяют методом графического или численного интегрирования.
При графическом интегрировании (рис. 1.5) задаются рядом значений  , промежуточных между величинами
, промежуточных между величинами  и
и  .
.
 |
Рис. 1.5. К расчету числа единиц переноса методом графического
интегрирования
Строят кривую зависимости  от
от  . Измеряют площадь, ограниченную крайними ординатами, соответствующими
. Измеряют площадь, ограниченную крайними ординатами, соответствующими  и
и  , и осью абсцисс (площадь
, и осью абсцисс (площадь  , заштрихованная на рисунке). После этого находят величину искомого интеграла с учетом масштабов
, заштрихованная на рисунке). После этого находят величину искомого интеграла с учетом масштабов  и
и  осей ординат и абсцисс:
осей ординат и абсцисс:
 .
.
Аналогично, пользуясь графиком зависимости  от
от 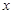 , определяют величину
, определяют величину  .
.
Для случаев, когда между равновесными концентрациями существует прямолинейная зависимость, при определении средней движущей силы используются более простые зависимости, вывод которых приведен в учебной литературе. Например, при расположении рабочей линии процесса выше линии равновесной для газовой и жидкой фаз зависимости для расчета средней движущей силы имеют вид
 ;
;

а для вычисления ЧЕП:
 ;
;
 ,
,
где  и
и  – тангенсы угла наклона рабочих и равновесных линий изменения концентраций.
– тангенсы угла наклона рабочих и равновесных линий изменения концентраций.
| <== предыдущая | | | следующая ==> |
| Ответ: ___ | | |
Date: 2016-01-20; view: 592; Нарушение авторских прав