Термодинамика потока в каналах переменного сечения

Рис. 2.10

Каналы переменного сечения, в которых происходит расширение рабочего тела и увеличение скорости потока, называются соплами (конфузорами). Они применяются для получения высоких скоростей и струй ударного действия.

Каналы переменного сечения, в которых происходит сжатие рабочего тела, сопровождающееся с ростом давления, называются диффузорами. Их используют в конструкциях насосов, вентиляторов и др.

Основой вывода общих закономерностей движения рабочего тела в каналах переменного сечения является уравнение неразрывности потока, которое при стационарном режиме движения (при G= const) имеет вид

const,

где f - площадь рассматриваемого сечения канала; ρ, v и w - плотность, удельный объем и скорость рабочего тела в этом сечении канала.

Если формулу (2.40) последовательно прологарифмировать и продифференцировать, получим уравнение неразрывности потока в дифференциальной форме

. (2.41)

Течение рабочего тела через канал (см.рис. 2.10) предполагается адиабатным . Это допущение объясняется ничтожной малостью тепловых потерь через стенки канала по сравнению с количеством теплоты, протекающей по каналу вместе с потоком рабочего тела. В данном случае справедливо применение уравнения адиабаты

const. (2.42)

Осуществляя процедуру логарифмирования и дифференцирования над этой зависимостью, находим

. (2.43)

Рассматривая совместно выражения (2.41 и 2.43) и используя уравнение (2.39), получаем

. (2.44)

Введя обозначения , , где а представляет скорость звука и M - число Маха, получаем уравнение неразрывности в виде

. (2.45)

Последнее уравнение учитывает зависимость скорости потока w от геометрической формы канала f и представляет математическую запись закона геометрического обращения воздействия.

Рис. 2.11

Характерные возможные случаи движения рабочего тела в каналах переменного сечения:

а) при М <1, если по ходу движения поток сужается (df<0), то скорость растет (dw>0), а при расширении канала (df>0), скорость потока уменьшается (dw<0);

б) при М>1 имеют место следующие случаи:

для df>0, dw>0;

для df<0, dw<0.

На рис. 2.11 представлен канал переменного сечения, который состоит из сужающегося участка (0<x≤а) и расширяющегося участка (а<х≤b). Подобным образом совмещенный канал носит название сопла Лаваля, который служит для получения сверхзвуковых скоростей.

Иллюстрированная на рис. 2.11 картина распределения давления и скорости потока вдоль сопла соответствует так называемому расчетному режиму работы сопла Лаваля. Этот режим имеет место при р₂=р_о, где р_о – давление окружающей среды и при условии, что в минимальном сечении сопла достигнута скорость потока, равной местной скорости звука.

При условии р₂ ≠ р_о – режимы течения газа и сопло Лаваля называются нерасчетными.

При р₂ > р_о – сопло называется недорасширенным;

При р₂ < р_о – перерасширенным.

При соблюдении условий расчетного режима сопло Лаваля позволяет получить сверхзвуковую скорость истечения. Конкретная сверхзвуковая скорость истечения зависит от значений параметров: р₁ и Т₁ – давления и температуры во входном сечении, - отношения площадей выходного и минимального сечений сопла, а также от давления окружающей среды р_о.

Следует отметить, что для того чтобы получить другую сверхзвуковую скорость истечения, не меняя параметров газа на входе в сопло р₁, Т₁, необходимо воспользоваться другим соплом с другим отношением выходного сопла к минимальному .

Очевидно, что если в минимальном сечении сопла не достигнута критическая скорость потока, то на всем протяжении сопла Лаваля будет дозвуковой режим движения, следовательно, скорость истечения из сопла также будет дозвуковая.

Истечение газов через сужающиеся сопла (конфузоры)

Рис. 2.12

На рис. 2.12 обозначены: р_i, v_i, w_i и f_i - давление, удельный объем, скорость газа в рассматриваемом сечении и площадь этого сечения. При i=1 указанные параметры соответствуют сечению I-I, а при i=2 - сечению II-II.

По отмеченной выше причине процесс течения газа через сопло предполагается адиабатным . При допущении, что и учитывая зависимость , уравнение первого закона термодинамики для потока можно представить в виде

.

Беря интеграл с обеих частей последнего уравнения, находим

.

В силу имеющегося условия f₁ >> f₂, w₂ >> w₁, можно пренебречь 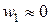и последнему уравнению придать вид

.

Из последнего выражения следует, что в конфузоре изменение кинетической энергии потока рабочего тела происходит лишь благодаря изменению его энтальпии.

Задача расчета конфузора сводится к определению w₂ при заданных значениях параметров р₁, v₁, р₂.

Перепишем последнее уравнение в виде

. (

Исходя из первого закона термодинамики для адиабатного процесса , определяем значение первого слагаемого правой части
уравнения:

.

Найденное выражение подставляем в предыдущее уравнение (и определяем w₂ – скорость истечения рабочего тела через сечение II - II

.

Далее используя эту формулу для скорости и уравнение неразрывности для потока , а также введя обозначение 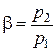, напишем соответствующие выражения для скорости потока и секундного массового расхода газа через сужающееся сопло в виде

,

.

Учитывая, что течение через конфузор адиабатное, напишем выражение для удельного объема газа на выходе из сопла

.

Подставив это выражение в предыдущую формулу, находим

.

Рассматривая эту формулу как функцию , исследуем ее на экстремум. В результате находим критическое значение β_кр, при котором массовый расход газа через конфузор имеет максимальное значение

.

Используя это выражение, определяем максимально возможную скорость газа на выходе из конфузора:

,

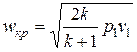которую можно выразить еще через критические параметры состояния:

,

тогда

,

где - скорость распространения звуковых волн в идеальном газе.

Распределению скорости вдоль сопла соответствуют условия

для 1>β≥β_кр, 0<w₂<w_кр;

для β_кр>β>0, w₂=w_кр.

Таким образом, скорость истечения из сужающегося сопла при критических условиях равна местной скорости звука. Поэтому скорость рабочего тела в конфузорах не может превышать скорости звука.

Аналогично можно получить выражение для максимального массового расхода через конфузор:

.

Как отмечалось выше, для получения сверхзвуковых скоростей необходимо использовать сопло Лаваля, в минимальном сечении которого скорость потока должна быть равна w_кр.

Расчет сужающейся части сопла Лаваля проводится точно так же, как и для обычного сужающегося дозвукового сопла. Площадь минимального сечения сопла определяется по заданному :

, откуда диаметр этого сечения будет равен .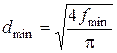

Длину сужающейся части сопла Лаваля обычно принимают равной диаметру минимального сечения сопла

.

Скорость на выходе из сопла Лаваля определяется формулой и площадь выходного сечения сопла Лаваля f₂ определяется из вышеприведенных уравнений, соответственно диаметр этого сечения вычисляется из выражения . Длину расширяющейся части сопла l₂ вычисляют по формуле

,

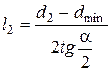где α - угол конусности расширяющейся части сопла Лаваля (колеблется в пределах 8 - 10^о).

Date: 2016-02-19; view: 1759; Нарушение авторских прав