Тема 8. Уравнения Максвелла для электромагнитного поля

Согласно теории Максвелла для электромагнитного поля в случае нестационарных (то есть, изменяющихся во времени) электрического и магнитного полей, источниками электрического поля могут быть либо электрические заряды, либо изменяющееся во времени магнитное поле, а источниками магнитного поля могут быть либо движущиеся электрические заряды (электрические токи), либо переменное электрическое поле.

В отличие от стационарных полей переменные электрическое и магнитное поля не являются независимыми друг от друга и рассматриваются как электромагнитное поле.

Уравнения Максвелла, как система уравнений, описывающих природу происхождения и свойства электрического и магнитного полей в случае электромагнитного поля имеет вид:

I. , то есть циркуляция вектора напряженности электрического поля определяется скоростью изменения вектора индукции магнитного поля ( - скорость изменения вектора индукции ).

Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

II. , то есть поток вектора электрического смещения 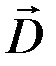через произвольную замкнутую поверхность S, равен алгебраической сумме зарядов, заключенных внутри объема V, ограниченного данной замкнутой поверхностью S (r - объемная плотность заряда).

III. , то есть циркуляция вектора напряженности 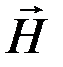по произвольному замкнутому контуру L определяется полным током I_полн., пронизывающим поверхность S, ограниченную данным контуром L.

- полный ток I_полн, складывающийся из тока проводимости I итока смещения I_см., то есть I_полн. = I + I_см..

Суммарный ток проводимости I определяется в общем случае через поверхностную плотность тока j () интегрированием, то есть

.

Ток смещения I_см, пронизывающий поверхность S, определяется в общем

случае через поверхностную плотность тока смещения () интегрированием, то есть: .

Введенное Максвеллом понятие «тока смещения», величина которого определяется скоростью изменения вектора электрического смещения 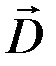, то есть величиной , показывает, что магнитные поля могут возбуждаться не только движущими­ся зарядами (электрическими токами проводимости), но и переменными электрическими полями.

IV. 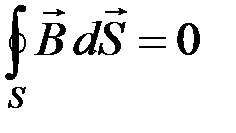, то есть поток вектора индукции магнитного поля через произвольную замкнутую поверхность S равен нулю.

Таким образом, уравнения Максвелла для электромагнитного поля:

I. ; II. ;

III. ; IV. .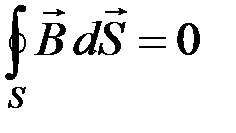

Векторные характеристики электрического поля 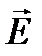и связаны между собой следующим соотношением: .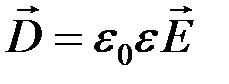

Векторные характеристики магнитного поля и 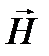связаны между собой следующим соотношением: .

Кроме того, вектора плотности тока проводимости и напряженности 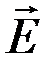, фигурирующие в уравнениях Максвелла, также связаны между собой:

,

где 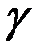– удельная проводимость вещества.

Уравнения Максвелла являются наиболее общими уравнениями для электрических и магнит­ных полей.

Тема 9. Электромагнитные колебания в колебательном контуре

Колебательный контур – это электрическая цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R. В идеальном колебательном контуре считается, что сопротивление R пренебрежимо мало (R» 0), что позволят в идеальном контуре (рис. 19),состоящем только изкатушки индуктивности и конденсатора, получить незатухающие электромагнитные колебания.

Рис. 19

Date: 2016-02-19; view: 377; Нарушение авторских прав