
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Заменив в (7.13) в соответствии с законом Ома , получим формулу
|
|
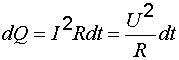 . (7.15)
. (7.15)
Соотношение (7.15) было установлено экспериментально в 1841 г. английским физиком Д. Джоулем и независимо от него в 1842 г. русским ученым Э. Х. Ленцем и
носит название закона Джоуля–Ленца: количество теплоты, выделяющейся в единицу времени на участке цепи, при протекании по нему постоянного тока, равно произведению сопротивления участка цепи на квадрат силы тока.
Поскольку величины, фигурирующие в формуле (7.15), являются интегральными (характеризующими проводник конечных размеров), то можно сказать, что выражение (7.15) описывает закон Джоуля–Ленца в интегральной форме.
От формулы (7.15), определяющей теплоту, выделяющуюся во всем проводнике, можно перейти к выражению, характеризующему выделение теплоты в различных местах проводника. Выделим в проводнике таким же образом, как это было сделано при выводе формулы (7.9), элементарный объем в виде цилиндра (см. рис. 7.1). Согласно закону Джоуля–Ленца за время 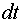 в этом объеме выделится теплота
в этом объеме выделится теплота
 , (7.16)
, (7.16)
где 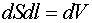 – элементарный объем.
– элементарный объем.
Разделив выражение (7.16) на 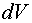 и
и 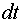 , найдем количество теплоты, выделяющееся в единице объема в единицу времени, – удельную тепловую мощность тока:
, найдем количество теплоты, выделяющееся в единице объема в единицу времени, – удельную тепловую мощность тока:
 . (7.17)
. (7.17)
Используя дифференциальную форму закона Ома [формула (7.9)] и соотношение  , получим
, получим
 . (7.18)
. (7.18)
Формула (7.18) представляет собой дифференциальную форму закона Джоуля–Ленца.
Отметим, что Джоуль и Ленц установили свой закон для однородного участка цепи. Однако, как следует из выкладок, приведенных в данном параграфе, формулы (7.15) и (7.18) справедливы и для неоднородного участка при условии, что действующие в нем сторонние силы имеют нехимическое происхождение.
§ 5. Разветвленные цепи. Правила Кирхгофа

| Расчет разветвленных электрических цепей значительно упрощается, если пользоваться правилами, сформулированными Кирхгофом. Этих правил два. Первое из них относится к узлам цепи. Узлом называется точка, в которой сходятся более чем два проводника (рис. 7.3). При этом ток, входящий в узел, считается положительным, а ток, выходящий из узла – отрицательным.
Первое правило Кирхгофа гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю:
 .(7.19) .(7.19)
|
Например (рис. 7.3), первое правило Кирхгофа запишется так:
 .
.
Первое правило вытекает из закона сохранения электрического заряда.
В случае установившегося постоянного тока ни в одной точке проводника не должны накапливаться электрические заряды. В противном случае токи не могли бы оставаться постоянными.
Уравнение (7.19) можно написать для каждого из N узлов цепи. Однако независимыми являются только N – 1 уравнений, N-e будет следствием из них.

| Второе правило относится к любому выделенному в разветвленной цепи замкнутому контуру (например, контур АВС на рис. 7.4). Зададим направление обхода (например, по часовой стрелке, на рис. 7.4). Если направление совпадает с направлением обхода контура, то ток считается положительным, а если не совпадает, – отрицательным. Применим к каждому из неразветвленных участков контура закон Ома:

|
При сложении этих выражений потенциалы взаимно уничтожаются и получается уравнение
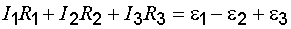 ,
,
которое выражает второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной цепи, алгебраическая сумма произведений сил токов  на сопротивления
на сопротивления  соответствующих участков этого контура равна алгебраической сумме эдс
соответствующих участков этого контура равна алгебраической сумме эдс  , встречающихся в этом контуре:
, встречающихся в этом контуре:
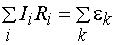 . (7.20)
. (7.20)
Уравнение (7.20) может быть составлено для всех замкнутых контуров, которые можно выделить мысленно в данной разветвленной цепи. Однако независимыми будут только уравнения для тех контуров, которые нельзя получить наложением других контуров один на другой.
При составлении уравнений второго правила Кирхгофа токам и эдс нужно приписывать знаки в соответствии с выбранным направлением обхода. Эдс также нужно приписать знак минус, так как она действует в направлении, противоположном направлению обхода. Направления обхода в каждом из контуров можно выбирать совершенно произвольно и независимо от выбора направлений в других контурах. При этом может случиться, что один и тот же ток либо одна и та же эдс войдет в разные уравнения с различными знаками. Это, однако, не имеет никакого значения, потому что изменение направления обхода вызывает лишь изменение всех знаков в уравнении (7.20) на обратные.
Число независимых уравнений, составленных в соответствии с первым и вторым правилами Кирхгофа, оказывается равным числу различных токов, текущих в разветвленной цепи. Поэтому, если заданы эдс и сопротивления для всех неразветвленных участков, то могут быть вычислены все токи.
Магнитное поле
Тема 3. Магнитное поле. Закон Био-Савара-Лапласа
Электрический ток создает поле, действующее на магнитную стрелку. Стрелка ориентируется по касательной к окружности, лежащей в плоскости, перпендикуляной к проводнику с током (рис. 9).
Основной характеристикой магнитного поля является вектор индукция 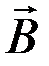 . Принято, что вектор индукция
. Принято, что вектор индукция 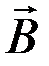 магнитного поля направлен в сторону север-ного полюса магнитной стрелки, помещенной в данную точку поля (рис. 9).
магнитного поля направлен в сторону север-ного полюса магнитной стрелки, помещенной в данную точку поля (рис. 9).
По аналогии с электрическим полем, магнитное поле также может быть изображено графически с помощью силовых линий (линий индукции магнитного поля).
Силовая линия – это такая линия, касательная к которой в каждой точке совпадает по направлению с вектором индукции 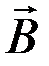 магнитного поля. Силовые линии магнитного поля, в отличие от силовых линий электростатического поля, являются замкнутыми и охватывают проводники с током. Направление силовых линий задается правилом правого винта (правилом буравчика): головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции (рис. 9).
магнитного поля. Силовые линии магнитного поля, в отличие от силовых линий электростатического поля, являются замкнутыми и охватывают проводники с током. Направление силовых линий задается правилом правого винта (правилом буравчика): головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции (рис. 9).
| I |

|
| N |
| S |
Рис. 9
Для нескольких источников магнитного поля согласно принципу суперпозиции магнитных полей индукция результирующего магнитного поля равна векторной сумме индукций всех отдельных магнитных полей:
 .
.
Вектор индукции 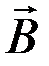 магнитного поля, создаваемого проводником с током
магнитного поля, создаваемого проводником с током  , можно определить с помощью закона Био-Савара-Лапласа. При этомнеобходимо учесть то, что закон Био-Савара-Лапласа позволяет найти модуль и направление лишьвектора индукции
, можно определить с помощью закона Био-Савара-Лапласа. При этомнеобходимо учесть то, что закон Био-Савара-Лапласа позволяет найти модуль и направление лишьвектора индукции  магнитного поля, создаваемого элементом проводника
магнитного поля, создаваемого элементом проводника 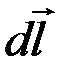 с током
с током  . Поэтому, для определения вектора индукции
. Поэтому, для определения вектора индукции 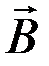 магнитного поля, создаваемого проводником с током
магнитного поля, создаваемого проводником с током  , необходимо первоначально разбить этот проводник на элементы проводника
, необходимо первоначально разбить этот проводник на элементы проводника 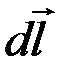 , для каждого элемента с помощью закона Био-Савара-Лапласа найти вектор индукции
, для каждого элемента с помощью закона Био-Савара-Лапласа найти вектор индукции  , а затем, используя принцип суперпозиции магнитных полей, сложить векторно все найденные вектора индукции
, а затем, используя принцип суперпозиции магнитных полей, сложить векторно все найденные вектора индукции  .
.
Закон Био-Савара-Лапласа в векторной форме:
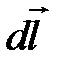
|
| I |

|
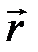
|
| М |
| Рис. 10 |
| α |
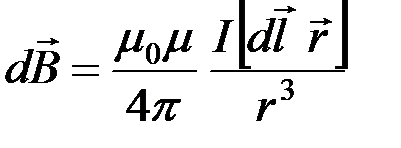 ,
,
где  – индукция магнитного поля в точке M, заданной радиусом-вектором
– индукция магнитного поля в точке M, заданной радиусом-вектором  , проведенным от начала вектора
, проведенным от начала вектора 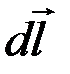 до этой точки;
до этой точки;
 – векторное произведение векторов
– векторное произведение векторов  и
и  ;
;
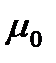 – магнитная постоянная,
– магнитная постоянная,
 – магнитная проницаемость среды.
– магнитная проницаемость среды.
Направление вектора 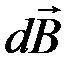 определяется по правилу правого винта: направление вращения головки винта дает направление вектора
определяется по правилу правого винта: направление вращения головки винта дает направление вектора 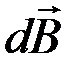 , если поступательное движение винта совпадает с направлением тока в элементе проводника (рис. 10).
, если поступательное движение винта совпадает с направлением тока в элементе проводника (рис. 10).
В скалярном виде закон Био-Савара-Лапласа:
 , где
, где  – угол между векторами
– угол между векторами 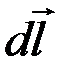 и
и  .
.
Магнитное поле линейного тока. Для нахождения индукции 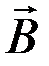 магнитного поля, созданного прямым проводником с током (рис. 11), необходимо разбить весь проводник на элементы
магнитного поля, созданного прямым проводником с током (рис. 11), необходимо разбить весь проводник на элементы 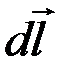 , для каждого элемента проводника
, для каждого элемента проводника 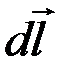 с током I найти вектор индукции
с током I найти вектор индукции  , а затем векторно сложить все найденные
, а затем векторно сложить все найденные 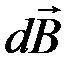 .
.
В произвольной точке М, удаленной от оси проводника на расстояние b (рис. 11), векторы 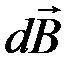 от всех элементов проводника
от всех элементов проводника 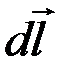 с током I имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов
с током I имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов 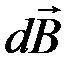 можно заменить сложением их модулей.
можно заменить сложением их модулей.
| I |
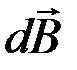
|
| α |
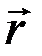
|

|
| D |

|
| а |
| b |
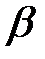
|
| М |
| С |
| О |
| Рис. 11 |
По закону Био-Савара-Лапласа модуль вектора магнитной индукции 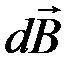 в точке М поля, созданного элементом проводника
в точке М поля, созданного элементом проводника 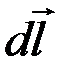 с током I:
с током I:
 .
.
В качестве переменной интегрирования выберем угол 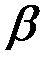 , выразив через этот угол все остальные величины.
, выразив через этот угол все остальные величины.
Из рисунка 11 следует, что  , а с другой стороны,
, а с другой стороны,  .
.
Тогда  , а модуль вектора магнитной индукции
, а модуль вектора магнитной индукции 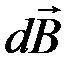 в точке М:
в точке М:
 .
.
Из прямоугольного треугольника DOM:
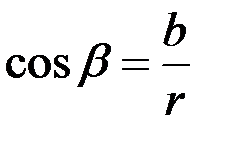 , откуда
, откуда 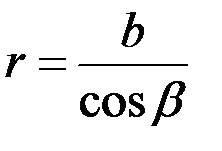 .
.
Следовательно, индукция dB, создаваемая элементом проводника dl с током I:
 .
.
Теперь можно перейти к интегрированию:
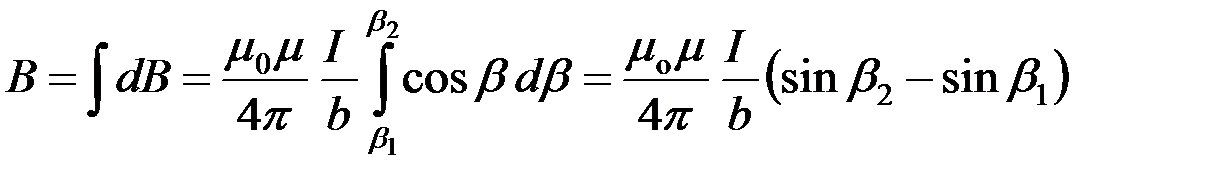 .
.
Так как угол  для прямого тока изменяется в пределах от
для прямого тока изменяется в пределах от 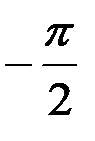 до
до  , то магнитная индукция поля прямого тока:
, то магнитная индукция поля прямого тока:
 .
.
Следовательно,
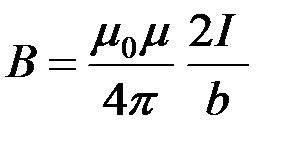 .
.
Магнитное поле в центре кругового проводника с током. Для нахождения индукции магнитного поля в центре кругового проводника с током необходимо разбить этот проводник на элементы  , причем все элементы проводника с током создают в центре кругового тока магнитные поля одинакового направления – вдоль нормали к плоскости витка (рис. 12). Поэтому сложение векторов
, причем все элементы проводника с током создают в центре кругового тока магнитные поля одинакового направления – вдоль нормали к плоскости витка (рис. 12). Поэтому сложение векторов 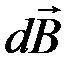 можно заменить сложением их модулей dB.
можно заменить сложением их модулей dB.
По закону Био-Савара-Лапласа модуль вектора 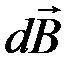 :
:
 .
.
Так как все элементы 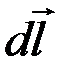 проводника перпендикулярны соответствующим радиусам-векторам
проводника перпендикулярны соответствующим радиусам-векторам 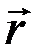 (рис. 12), то sin a = 1 для всех элементов
(рис. 12), то sin a = 1 для всех элементов 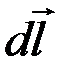 . Расстояния r для всех элементов проводника
. Расстояния r для всех элементов проводника 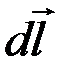 также одинаковые (r = R).
также одинаковые (r = R).
Тогда выражение для модуля вектора 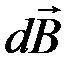 примет вид:
примет вид:
 .
.
Теперь для нахождения модуля вектора 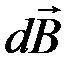 можно перейти к интегрированию:
можно перейти к интегрированию:
 .
.
Следовательно, индукция магнитного поля B в центре кругового проводника радиусом R с током I:
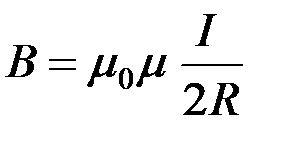 .
.
Тема 4. Действие магнитного поля на проводник с током (закон Ампера) и на движущийся заряд (сила Лоренца)
Закон Ампера. На элемент проводника 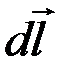 с током I, помещённый в магнитное поле с индукцией
с током I, помещённый в магнитное поле с индукцией 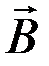 действует сила
действует сила 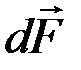 (
(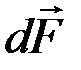 – сила Ампера):
– сила Ампера):  .
.
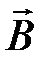
|

|
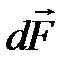
|

|
| Рис. 13 |

|
| I |
| I |
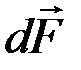 :
: 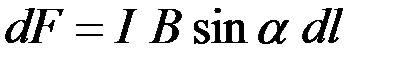 ,
,
где 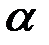 – угол между векторами
– угол между векторами 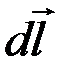 и
и 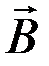 .
.
Направление вектора  можно определить по правилу левой руки: если силовые линии входят в ладонь, а четыре вытянутых пальца располагаются по току, то отведённый большой палец укажет направление силы Ампера (рис. 13, сила
можно определить по правилу левой руки: если силовые линии входят в ладонь, а четыре вытянутых пальца располагаются по току, то отведённый большой палец укажет направление силы Ампера (рис. 13, сила  перпендикулярна плоскости рисунка).
перпендикулярна плоскости рисунка).
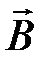
|

|
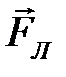
|
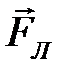
|
| q |
| q |

|
 в магнитном поле с индукцией
в магнитном поле с индукцией 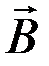 , действует сила
, действует сила 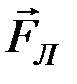 (
(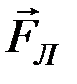 – сила Лоренца):
– сила Лоренца):  .
.
Модуль вектора  :
:  ,
,
где α – угол между векторами  и
и 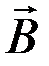 .
.
| Рис. 14 |
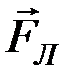 может быть определено по правилу левой руки для движущихся положительных зарядов и по правилу правой руки для движущихся отрицательных зарядов: если силовые линии магнитного поля входят в ладонь, а четыре вытянутых пальца располагаются по скорости движения частицы, то отведённый большой палец укажет направление силы Лоренца (рис.14, сила
может быть определено по правилу левой руки для движущихся положительных зарядов и по правилу правой руки для движущихся отрицательных зарядов: если силовые линии магнитного поля входят в ладонь, а четыре вытянутых пальца располагаются по скорости движения частицы, то отведённый большой палец укажет направление силы Лоренца (рис.14, сила  перпендикулярна плоскости рисунка).
перпендикулярна плоскости рисунка). Тема. 5. Магнитный поток. Теорема Гаусса для магнитного поля
Поток вектора магнитной индукции  ( или магнитный поток) через произвольную площадку S характеризуется числом силовых линий магнитного поля, пронизывающих данную площадку S. Если площадка S расположенаперпендикулярно силовым линиям магнитного поля (рис. 15), то поток ФB
( или магнитный поток) через произвольную площадку S характеризуется числом силовых линий магнитного поля, пронизывающих данную площадку S. Если площадка S расположенаперпендикулярно силовым линиям магнитного поля (рис. 15), то поток ФB
вектора индукции  через данную площадку S:
через данную площадку S:  .
.
| S |

|
| S |

|
| α |

|
Рис. 15 Рис. 16
Если площадка S расположена неперпендикулярно силовым линиям магнитного поля (рис. 16), то поток ФB вектора индукции  через данную площадку S:
через данную площадку S:
 ,
,
где α – угол между векторами  и нормали
и нормали 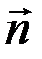 к площадке S.
к площадке S.
| dS |

|

|
| α |
| S |

|
| Рис. 17 |
 через произвольную поверхность S, необходиморазбить эту поверхность на элементарные площадки dS (рис. 17)иопределить элементарный поток
через произвольную поверхность S, необходиморазбить эту поверхность на элементарные площадки dS (рис. 17)иопределить элементарный поток  вектора
вектора  через каждую площадку dS по формуле:
через каждую площадку dS по формуле:  ,
,
где α – угол между векторами  и нормали
и нормали  к данной площадке dS;
к данной площадке dS;
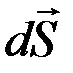 – вектор, равный по величине площади площадки dS и направленный по вектору нормали
– вектор, равный по величине площади площадки dS и направленный по вектору нормали 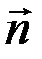 к данной площадке dS.
к данной площадке dS.
Тогда поток вектора  через произвольную поверхность S равен алгебраической сумме элементарных потоков
через произвольную поверхность S равен алгебраической сумме элементарных потоков  через все элементарные площадки dS, на которые разбита поверхность S, что приводит к интегрированию:
через все элементарные площадки dS, на которые разбита поверхность S, что приводит к интегрированию:
 .
.
Теорема Гаусса для магнитного поля
| S |
| Рис. 18 |

|
| α |
| dS |

|

|
 магнитного поля через эту поверхность S можно рассчитать по формуле:
магнитного поля через эту поверхность S можно рассчитать по формуле:
 .
.
С другой стороны, число линий магнитной индукции, входящих внутрь объема, ограниченного этой замкнутой поверхностью, равно числу линий, выходящих из этого объема (рис. 18). Поэтому, с учетом того, что поток вектора индукции  магнитного поля считается положительным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, суммарный поток ФB вектора индукции
магнитного поля считается положительным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, суммарный поток ФB вектора индукции  через произвольную замкнутую поверхность S равен нулю, то есть:
через произвольную замкнутую поверхность S равен нулю, то есть:
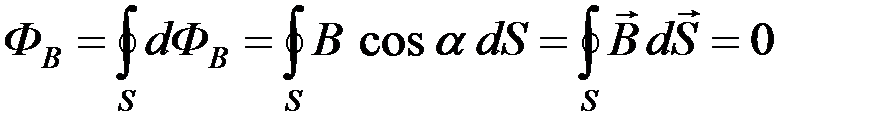 ,
,
что составляет формулировку теоремы Гаусса для магнитного поля.
Тема. 6. Явление электромагнитной индукции. Закон Фарадея
Явление возникновения электрического тока в замкнутом проводящем контуре в результате изменения магнитного потока, пронизывающего этот контур, называется явлением электромагнитной индукции. Возникновение индукционного электрического тока в контуре указывает на наличие в этом контуре электродвижущей силы, называемой электродвижущей силой (ЭДС) электромагнитной индукции.
Согласно закону Фарадея, величина ЭДС электромагнитной индукции  определяется только скоростью изменения магнитного потока, пронизывающего проводящий контур, а именно:
определяется только скоростью изменения магнитного потока, пронизывающего проводящий контур, а именно:
величина ЭДС электромагнитной индукции  прямо пропорциональна скорости изменения магнитного потока, пронизывающего проводящий контур:
прямо пропорциональна скорости изменения магнитного потока, пронизывающего проводящий контур:
 (закон Фарадея).
(закон Фарадея).
Направление индукционного тока в контуре определяется по правилу Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое этим током магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток.
Закон Фарадея с учетом правила Ленца можно сформулировать следующим образом: величина ЭДС электромагнитной индукции 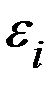 в контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром, то есть:
в контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром, то есть:
 (закон Фарадея с учетом правила Ленца).
(закон Фарадея с учетом правила Ленца).
Тема 7. Циркуляция вектора магнитной индукции 
Циркуляцией вектора магнитной индукции  по произвольному замкнутому контуру L называется интеграл:
по произвольному замкнутому контуру L называется интеграл:
 .
.
Для того, чтобы найти циркуляцию вектора магнитной индукции  по произвольному замкнутому контуру L, необходимо выбрать направление обхода контура, разбить этот контур L на элементы
по произвольному замкнутому контуру L, необходимо выбрать направление обхода контура, разбить этот контур L на элементы  , для каждого элемента
, для каждого элемента  рассчитать величину
рассчитать величину  (a – угол между векторами
(a – угол между векторами  и
и  ), а затем все эти величины сложить, что приводит к искомому интегралу.
), а затем все эти величины сложить, что приводит к искомому интегралу.
Однако циркуляцию вектора  по произвольному замкнутому контуру L можно рассчитать, используя теорему о циркуляции вектора
по произвольному замкнутому контуру L можно рассчитать, используя теорему о циркуляции вектора  .
.
Теорема о циркуляции вектора  : циркуляция вектора
: циркуляция вектора  по произвольному замкнутому контуру L равна произведению магнитной постоянной m 0 на алгебраическую сумму токов, охватываемых этим контуром L:
по произвольному замкнутому контуру L равна произведению магнитной постоянной m 0 на алгебраическую сумму токов, охватываемых этим контуром L:
 ,
,
где n – число проводников с токами, охватываемых контуром L. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным.
Величина  , где a – угол между векторами
, где a – угол между векторами  и
и  может быть записана в виде скалярного произведения векторов
может быть записана в виде скалярного произведения векторов  и
и  , то есть, как
, то есть, как  , а полученное соотношение для циркуляции вектора
, а полученное соотношение для циркуляции вектора  примет вид:
примет вид:
 .
.
Магнитное поле претерпевает изменения при переходе из одного вещества в другое, что определяется магнитными свойствами вещества, которые характеризуются величиной магнитной проницаемости среды (m).
Кроме вектораиндукции  магнитного поля, учитывающего магнитные свойства вещества, для описания магнитного поля введен также и вектор напряженности
магнитного поля, учитывающего магнитные свойства вещества, для описания магнитного поля введен также и вектор напряженности  магнитного поля, причем для однородной изотропной среды вектор магнитной индукции
магнитного поля, причем для однородной изотропной среды вектор магнитной индукции  связан с вектором напряженности
связан с вектором напряженности  магнитного поля следующим соотношением:
магнитного поля следующим соотношением:
 ,
,
где m 0 – магнитная постоянная, m – магнитная проницаемость среды.
Поскольку для вакуума m = 1, то с учетом приведенного соотношения может быть получена циркуляция вектора напряженности 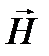 по произвольному замкнутому контуру L в следующем виде:
по произвольному замкнутому контуру L в следующем виде:
 ,
,
то есть циркуляция вектора 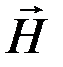 по произвольному замкнутому контуру L равна алгебраической сумме токов, охватываемых этим контуром L.
по произвольному замкнутому контуру L равна алгебраической сумме токов, охватываемых этим контуром L.
Сравнивая векторные характеристики электростатического (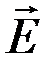 и
и  ) и магнитного (
) и магнитного ( и
и  ) полей, следует отметить, что аналогом вектора напряженности
) полей, следует отметить, что аналогом вектора напряженности  электростатического поля является вектор магнитной индукции
электростатического поля является вектор магнитной индукции  , так как векторы
, так как векторы  и
и  определяют силовые действия этих полей и зависят от свойств среды, а аналогом вектора электрического смещения
определяют силовые действия этих полей и зависят от свойств среды, а аналогом вектора электрического смещения 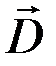 является вектор напряженности
является вектор напряженности  магнитного поля.
магнитного поля.
Date: 2016-02-19; view: 446; Нарушение авторских прав