Геометрическое представление сигналов

Литература: [Л.1], с 23-29

[Л.2], с 30-32

В современной теории радиотехнических сигналов широкое применение находят геометрические представления сигналов, использующие такие понятия как пространство, вектор, расстояние, проекция и т.д. Поэтому, для уяснения сущности геометрического представления необходимо познакомиться с этими понятиями.

Как уже подчеркивалось выше, для передачи сообщений в РТИС используется множество сигналов , образующее ансамбль сигналов. Это множество может быть непрерывным (континуальным), либо дискретным (счетным). В свою очередь дискретные множества могут быть конечными, либо бесконечными. При геометрическом представлении говорят, что множество образует пространство сигналов.

Любое пространство предполагает наличие системы координат. Пространство, в котором обитает человек, характеризуется декартовой системой координат, характеризующейся наличием трех взаимно перпендикулярных координатных осей. Тогда с любой точкой пространства будут связаны три вещественных числа, которые можно рассматривать как координаты точки в пространстве.

Рассмотрим как можно распространить указанные понятия на радиотехнические сигналы. В качестве примера приведем представление произвольного сигнала длительностью в виде суммы двух неперекрывающихся прямоугольных импульсов с высотой соответственно и и длительностью (рис 1.8).

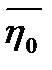Т.к. импульсы не перекрываются во времени (проекция одного импульса на другой по оси времени равна нулю), то совокупность двух импульсов, отображающих сигнал , можно представить точкой в двумерной системе координат, образованной взаимноперпендикулярными векторами и (рис.1.9). Отрезок прямой, проведенный из начала системы координат в точку с координатами и представляет собой вектор сигнала при его данном динамическом представлении. Тогда математически его можно записать в виде

.

Если представить тремя импульсами, то сигнал 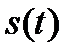будет отображаться вектором в трехмерном пространстве, четырьмя импульсами-вектором в четырехмерном пространстве, n импульсами-вектором в n-мерном пространстве. Таким образом, в общем случае сигнал отображается вектором в абстрактном n-мерном пространстве. При этом пространство может быть бесконечномерным.

Отметим, что совокупность векторов образуют координатный базис пространства. Очевидно, с изменением значений сигнала во времени длина вектора и его положение в пространстве будет также меняться.

Для дальнейшего рассмотрения геометрического представления зафиксируем момент времени , т.е. сделаем как бы фотографический снимок пространства. Это позволит на время абстрагироваться от динамики изменения сигнала и рассмотреть свойства пространства, используемого для геометрического представления. Кроме того, при характеристике пространства будем использовать его n-мерную модель, а для графических иллюстраций - двумерное пространство.

Исходя из этих предположений, вектор сигнала можно записать следующим образом

. (1.20)

В теории радиотехнических сигналов пространство для геометрического представления должно быть линейным.

Линейное пространство обладает следующими основными свойствами:

- если векторы и принадлежат пространству 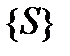, то и вектор также принадлежит этому пространству, причем (рис.1.10)

; (1.21)

Рис. 1.10

- определена операция умножения вектора на любое вещественное число , причем

; (1.22)

- пространство содержит нулевой элемент , причем

. (1.23)

Поскольку при анализе сигналов, как правило, пользуются количественными характеристиками, пространство геометрического представления должно позволять определять длину векторов для их сравнения. Длину вектора называют нормой , а пространство, в котором определена норма - нормированным пространством. Основными свойствами линейного нормированного пространства являются:

- для любого вещественного числа норма

; (1.24)

- если и - два вектора, принадлежащие линейному нормированному пространству, то:

. (1.25)

Свойство (1.25) отображает так называемое правило треугольника, известное из курса геометрии, в справедливости которого можно убедиться из рис.1.10.

В качестве нормы в теории радиотехнических сигналов исполь­зуют величину

. (1.26)

Очевидно квадрат нормы

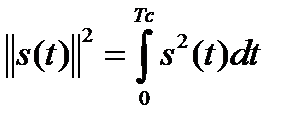, представляет собой энергию сигнала.

Введение понятия нормы позво­ляет определять длину векторов, представляющих сигналы в линей­ном нормированном пространстве, но не позволяет определять рас­стояние между векторами. Для того чтобы это стало возможным не­обходимо ввести понятие расстояния между векторами и , т.е. величину , называемую метрикой. Тогда линейное нормирован­ное пространство становится метрическим. Метрика про­странства должна удовлетворять условиям:

- расстояние между одинаковыми векторами равно нулю, т.е.

; (1.27)

- расстояние между векторами и , должно быть равно рас­стоянию между и , т.е.

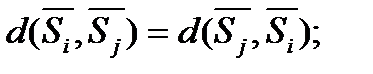(1.28)

- должно выполняться правило треугольника, т.е.

. (1.29)

В ТРТС в качестве метрики ис­пользуют норму разности двух сигналов

. (1.30)

Нетрудно убедиться, что величина (1.30) удовлетворяет всем аксиомам метрического пространства.

И, наконец, взаимное расположение двух векторов в пространстве оценивается величиной угла между ними, который определяется выражением

, (1.31)

где числитель представляет собой скалярное произведение векторов.

Таким образом, для геометрического представления сигналов в радиотехнике используется линейное метрическое нормированное пространство. Если пространство конечномерное (координатный базис содержит конечное число векторов ), то такое пространство называют Евклидовым. Бесконечномерное пространство называется Гильбертовым пространством.

Date: 2016-02-19; view: 907; Нарушение авторских прав