предельных состояний

Общие положения

При проектировании железобетонных конструкций следует обеспечивать не только их прочность, но и необходимую трещиностойкость и жёсткость. Расчёты железобетонных конструкций по второй группе предельных состояний должны обеспечивать их нормальную эксплуатацию.

Расчёты производят на действие расчётных нагрузок с коэффициентами надёжности по нагрузке 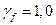(численно равными нормативным нагрузкам) при расчётных сопротивлениях материалов для предельных состояний второй группы (численно равными нормативным сопротивлениям).

Трещиностойкость железобетонных конструкций – это их сопротивляемость образованию и раскрытию трещин, которые могут быть вызваны внешней нагрузкой, температурными или усадочными деформациями.

Трещиностойкость железобетонных конструкций обеспечивают исходя из следующих требований:

- из условия сохранности арматуры (для любых конструкций);

- из условия ограничения проницаемости конструкций (для конструкций, подверженных непосредственному давлению жидкостей газов, сыпучих тел).

Для выполнения этих требований в зависимости от условий эксплуатации конструкций нормами установлены значения предельно допустимой ширины раскрытия трещин, которые принимают равными:

а) из условия сохранности арматуры:

- классов А240-А600, В500:

0,3 мм - при продолжительном раскрытии трещин;

0,4 мм - при непродолжительном раскрытии трещин;

- классов А800, А1000, а также Вр1200-Вр140, К1400, К1500 (К-19) и К1500 (К-7) диаметром 12 мм:

0,2 мм - при продолжительном раскрытии трещин;

0,3 мм - при непродолжительном раскрытии трещин;

- классов Вр1500, К1500 (К-7) диаметром 6 и 9 мм:

0,1 мм - при продолжительном раскрытии трещин;

0,2 мм - при непродолжительном раскрытии трещин;

б) из условия ограничения проницаемости конструкций:

0,2 мм – при продолжительном раскрытии трещин;

0,3 мм – при непродолжительном раскрытии трещин.

Непродолжительное раскрытие трещин определяют от совместного действия постоянных и временных (кратковременных и длительных) нагрузок.

Продолжительное раскрытие трещин определяют от совместного действия постоянных и временных длительных нагрузок.

Расчёт трещиностойкости железобетонного элемента выполняют для сечений нормальных и наклонных к продольной оси элемента. Он включает в себя:

1. Расчёт по образованию трещин;

2. Расчёт по раскрытию трещин.

Если в конструкциях трещины не образуются, то расчёт по раскрытию трещин не производят.

Жёсткость железобетонных конструкций – это их сопротивляемость деформациям, которые могут быть вызваны внешней нагрузкой, температурными или осадочными воздействиями.

Для обеспечении необходимой жёсткости элементов нормами установлены предельные значения перемещений исходя из следующих требований:

а) технологических (обеспечение условий нормальной эксплуатации технологического и подъёмно-транспортного оборудования, контрольно-измерительных приборов т.д.);

б) конструктивных (обеспечение целостности примыкающих друг к другу элементов конструкций и их стыков, обеспечение заданных уклонов);

в) физиологических (предотвращение вредных воздействий и ощущений дискомфорта при колебаниях);

г) эстетико- психологических (обеспечение благоприятных впечатлений от внешнего вида конструкции, предотвращение ощущения опасности).

Каждое из указанных требований должно быть выполнено независимо от других.

При ограничении деформаций технологическими или конструктивными требованиями расчёт следует производить на действие постоянных и временных (кратковременных и длительных) нагрузок, при ограничении деформаций эстетико- психологическими требованиями – на действие постоянных и временных длительных нагрузок.

Расчёт железобетонных элементов по деформациям включает:

1. Расчёт по прогибам;

2. Расчёт углов сдвига.

2. Расчёт железобетонных конструкций по трещиностойкости

2.1. Расчёт по образованию трещин

Данный расчёт производят для проверки необходимости расчёта по раскрытию трещин и необходимости учёта трещин при расчёте по деформациям.

В основу расчёта положена стадия I^а напряжённо-деформированного состояния элемента со следующими предпосылками:

1. Распределение относительных деформаций бетона и арматуры по высоте сечения элемента принимают по линейному закону, т.е. считают справедливой гипотезу плоских сечений.

2. Криволинейную эпюру напряжений в бетоне растянутой зоны заменяют прямоугольной с напряжением равным пределу прочности бетона на растяжение .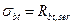

3. Наибольшие относительные удлинения крайнего растянутого волокна бетона принимают равной его предельной растяжимости

.

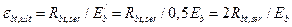4. Эпюру напряжений в сжатом бетоне принимают треугольной.

5. Напряжения в растянутой арматуре принимают равными

,

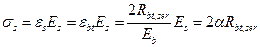где - отношение модулей упругости арматуры и бетона.

Для центрально растянутых элементов расчёт заключается в проверке условия, что трещины в сечениях, нормальных к продольной оси, не образуются, если продольная сила от действия внешней нагрузки не превосходит внутреннего продольного усилия в сечении перед образованием трещин 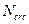, т.е.:

,

где - растягивающее усилие в элементе от внешней нагрузки;

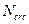- усилие, воспринимаемое сечением элемента при образовании трещин.

.

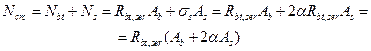Для изгибаемых элементов расчёт заключается в проверке условия, что трещины в сечениях, нормальных к продольной оси, не образуются, если момент внешних сил 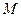не превосходит момента внутренних усилия в сечении перед образованием трещин 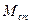, т.е.:

,

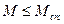где 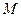- изгибающий момент в элементе от внешней нагрузки;

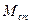- момент, воспринимаемый сечением элемента при образовании трещин.

,

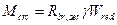где 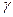- коэффициент, учитывающий влияние пластических деформаций бетона растянутой зоны, и, зависящий от формы поперечного сечения элемента, (для прямоугольного и таврового сечения с полкой в сжатой зоне );

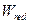- момент сопротивления приведённого сечения элемента.

Приведённым называют сечение, в котором материал арматуры приведён к материалу бетона, с помощью соотношения модулей упругости арматуры и бетона (рис. 32).

Рис. 32. К определению момента сопротивления приведённого

сечения элемента.

Момент сопротивления приведённого сечения элемента определяют в следующей последовательности:

1. Площадь приведённого сечения равна

.

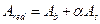2. Статический момент приведённого сечения относительно крайнего растянутого волокна сечения

.

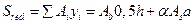3. Расстояние от крайнего растянутого волокна сечения до центра тяжести приведённого сечения

.

4. Момент инерции приведённого сечения относительно главных осей, проходящих через его центр тяжести

.

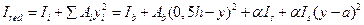5. Момент сопротивления приведённого сечения элемента

.

2.2. Расчёт по раскрытию трещин

Расчёт железобетонных элементов производят по непродолжительному раскрытию трещин и продолжительному раскрытию трещин из условия ,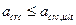

где а_{crc ,} - ширина раскрытия трещин от внешней нагрузки;

а_crc,ult - предельно допустимая ширина раскрытия трещин по нормам.

Ширину раскрытия трещин (а_crc) определяют исходя из взаимных смещений растянутой арматуры и бетона по обе стороны трещины на уровне оси арматуры и принимают:

- при продолжительном раскрытии

a_crc = a_crc,1,

- при непродолжительном раскрытии

a_crc = a_crc,1 + a_crc,2 - a_crc,3,

где а_crc,1 - ширина раскрытия трещин от продолжительного действия постоянных и временных длительных нагрузок;

а_crc,2 - ширина раскрытия трещин от непродолжительного действия постоянных и временных (длительных и кратковременных) нагрузок;

а_crc,3 - ширина раскрытия трещин от непродолжительного действия постоянных и временных длительных нагрузок.

Ширину раскрытия трещин нормальных к продольной оси элемента определяют по формуле

,

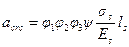где φ ₁ - коэффициент, учитывающий продолжительность действия нагрузки и принимаемый равным:

1,0 - при непродолжительном действии нагрузки;

1,4 - при продолжительном действии нагрузки;

φ ₂ - коэффициент, учитывающий профиль продольной арматуры и принимаемый равным:

0,5 - для арматуры периодического профиля и канатной;

0,8 - для гладкой арматуры;

φ ₃ - коэффициент, учитывающий характер нагружения и принимаемый равным:

1,0 - для изгибаемых и внецентренно сжатых элементов;

1,2 - для растянутых элементов.

ψ_s - коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами:

если 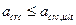- ψ_s = 1,0;

если - .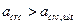

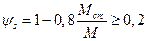σ_s - напряжение в продольной растянутой арматуре в нормальном сечении с трещиной от соответствующей внешней нагрузки, определяемое по формуле

l_s - базовое (без учета влияния вида поверхности арматуры) расстояние между смежными нормальными трещинами, которое определяют по формуле

и принимают не менее 10 d_s и 100 мм и не более 40 d_s и 400 мм (для элементов с рабочей высотой поперечного сечения не более 1 м).

Здесь A_bt - площадь сечения растянутого бетона. При этом высота растянутой зоны бетона принимается не менее 2 а и не более 0,5 h.

3. Расчёт железобетонных конструкций по деформациям

3.1. Расчёт по прогибам

Расчёт железобетонных элементов по прогибам производят из условия:

,

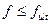где f - прогиб железобетонного элемента от действия внешней нагрузки;

f_ult - значение предельно допустимого прогиба железобетонного элемента по нормам.

Прогибы железобетонных конструкций определяют по общим правилам строительной механики в зависимости от изгибных, сдвиговых и осевых деформационных характеристик железобетонных элементов в сечениях по его длине.

Для изгибаемых элементов прогиб определяют по формуле:

,

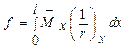где - изгибающий момент в сечении х от действия единичной силы, приложенной в сечении, для которого определяется прогиб, в направлении этого прогиба;

- полная кривизна элемента в сечении от внешней нагрузки, при которой определяется прогиб.

В общем случае данную формулу можно реализовать путем разбиения элемента на ряд участков, определяя кривизну на границах этих участков (с учетом наличия или отсутствия трещин и знака кривизны) и перемножения эпюр моментов и кривизны 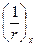по длине элемента, принимая линейное распределение кривизны в пределах каждого участка.

Для изгибаемых элементов постоянного сечения, имеющих трещины на каждом участке, в пределах которого изгибающий момент не меняет знак, допускается вычислять кривизну для наиболее напряженного сечения и принимать для остальных сечений такого участка кривизны изменяющимися пропорционально значениям изгибающего момента (рис. 33).

В этом случае для свободно опертых и консольных элементов максимальный прогиб определяют по формуле

,

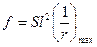где 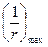- полная кривизна в сечении с наибольшим изгибающим моментом, от нагрузки, при которой определяют прогиб;

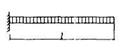
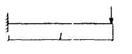
S - коэффициент, зависящий от расчётной схемы элемента и вида нагрузки, некоторые значения которого приведены в таблице 15.

Таблица 15

Схема загружения свободно опертой балки	Коэффициент S	Схема загружения консоли	Коэффициент S
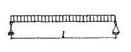
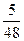
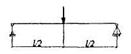
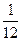
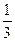
Примечание. При загружении элемента сразу по нескольким схемам , где Si и Mi – соответственно коэффициент S и момент M в середине пролета балки или в заделке консоли для каждой схемы загружения. В этом случае кривизну 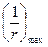определяют при значении М равном Σ Mi

Рис. 33. Эпюры изгибающих моментов и кривизны в железобетонном элементе постоянного сечения

а - схема расположения нагрузки; б - эпюра моментов; в - эпюра кривизны

Полную кривизну изгибаемых, внецентренно сжатых и внецентренно растянутых элементов для участков без трещин в растянутой зоне определяют по формуле:

где 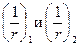- кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и длительных нагрузок.

Кривизну железобетонного элемента на участке без трещин определяют по формуле

где М - изгибающий момент от внешней нагрузки (включая момент от продольной силы N относительно оси, проходящей через центр тяжести приведенного сечения);

D - изгибная жесткость приведенного поперечного сечения элемента, определяемая по формуле:

,

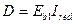I_red - момент инерции приведенного сечения относительно его центра тяжести;

E_{b 1} - модуль деформации сжатого бетона, принимаемый:

при непродолжительном действии нагрузки E_{b 1} = 0,85 E_b;

при продолжительном действии нагрузки ,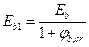

где φ_b,cr - коэффициент ползучести бетона, принимаемый в зависимости от относительной влажности воздуха и класса бетона.

Полную кривизну изгибаемых, внецентренно сжатых и внецентренно растянутых элементов для участков с трещинами в растянутой зоне определяют по формуле:

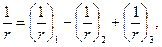
где 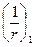- кривизна от непродолжительного действия всех нагрузок, на которые производят расчет по деформациям;

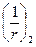- кривизна от непродолжительного действия постоянных ивременных длительных нагрузок;

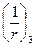- кривизна от продолжительного действия постоянных и временных длительных нагрузок.

Кривизну железобетонного элемента на участке с трещинами определяют по той же формуле:

Изгибная жесткость приведенного сечения элемента равна

,

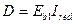где I_red - момент инерции приведенного сечения относительно его центра тяжести без учёта растянутой зоны бетона;

E_{b 1} - модуль деформации сжатого бетона, принимаемый равным

,

Значения относительных деформаций ε _b1,red принимают:

- при непродолжительном действии нагрузки ε _b1,red = 0,0015;

- при продолжительном действии нагрузки – в зависимости от относительной влажности воздуха окружающей среды ε _b1,red = 0,0024-0,0034.

Значение коэффициента приведения арматуры к бетону в данном случае принимают равным .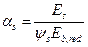

3.2. Расчёт углов сдвига элемента

Угол деформации сдвига определяется по формуле

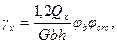
где Q_x - поперечная сила в сечении х от внешней нагрузки;

G - модуль сдвига бетона равный ;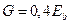

φ_b - коэффициент, учитывающий влияние ползучести бетона и принимаемый равным:

- при продолжительном действии нагрузок φ_b = 1 + φ_b,cr

- при непродолжительном действии нагрузок φ_b = 1,0;

φ_crс - коэффициент, учитывающий влияние трещин на деформации сдвига и принимаемый равным:

- на участках по длине элемента, где отсутствуют нормальные и наклонные к продольной оси элемента трещины, - φ_crс = l,0;

- на участках, где имеются только наклонные трещины, - φ_crс = 4,0;

- на участках, где имеются только нормальные или нормальные и наклонные трещины, коэффициент φ_crс определяется по формуле

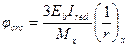
где М_х и 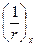- соответственно момент и кривизна от внешней нагрузки при непродолжительном ее действии;

I_red - момент инерции приведенного сечения.

литература

1. СНиП 2.01.07-85*. Нагрузки и воздействия [Текст]: утв. Госстроем России 29.05.2003: взамен СНиП II-6-74: дата введения 01.01.87. – М.:ГУП ЦПП, 2003.- 44 с.

2. СНиП 52-01-2003. Бетонные и железобетонные конструкции. Основные положения [Текст]:утв. Государственным комитетом Российской Федерации по строительству и жилищно-коммунальному комплексу от 30.06.2003: взамен СНиП 2.03.01-84: дата введ. 01.03.2004.-М.:ГУП НИИЖБ, 2004.-26с.

3. СП 52-101-2003. Бетонные и железобетонные конструкции без предварительного напряжения арматуры [Текст]:утв. Государственным комитетом Российской Федерации по строительству и жилищно-коммунальному комплексу от 30.06.2003: взамен СНиП 2.03.01-84: дата введ. 01.03.2004.-М. ГУП НИИЖБ, 2004.-55с.

4. ПОСОБИЕ К СП 52-102-2004. По проектированию предварительно напряжённых железобетонных конструкции из тяжёлого бетона [Текст]:утв.ОАО «ЦНИИпромзданий» от 01.01.2005: взамен Пособия к СНиП 2.03.01-84: дата введ. 01.01.2005.-М. ГУП НИИЖБ, 2005.-158с.

5. Байков, В. Н., Железобетонные конструкции. Общий курс [Текст]: учеб. для вузов /В. Н. Байков,. Э. Е. Сигалов. Изд. 5-е, перераб. и доп. – М.: Стройиздат, 1991.-767 с.: ил.

6. Бондаренко, В. М., Железобетонные и каменные конструкции. [Текст]: учеб. для строит. спец. вузов /В. М. Бондаренко, Р. О. Бакиров, В. Г. Назаренко, В. И. Римшин; Под ред. В. М. Бондаренко. Изд. 3, исправл.- М.: Высш. шк., 2004.-876 с.: ил.

Содержание

Введение ………………………………………………………….………3

А. Расчёт железобетонных конструкций по первой группе

предельных состояний……………….……………………….……….4

I. Расчёт и конструирование изгибаемых элементов …………….....4

1. Классификация изгибаемых элементов ……………………….4

2. Основы конструирования изгибаемых элементов ……………5

3. Расчёт изгибаемых элементов на прочность по сечениям

нормальным к продольной оси элемента ………………..…..11

3.1. Предпосылки расчёта на прочность по нормальным

сечениям ………………………………….………..…..…11

3.2. Расчёт изгибаемых элементов прямоугольного

сечения с одиночной арматурой ………………………..13

3.3. Расчет изгибаемых элементов таврового сечения с

одиночной арматурой …………………………..……….19

4. Расчёт изгибаемых элементов на прочность по

сечениям наклонным к продольной оси элемента ………28

4.1. Общие положения ……………………………..………28

4.2. Расчёт изгибаемых элементов по полосе между

наклонными сечениями ……………………………………30

4.3. Расчёт изгибаемых элементов по наклонным

сечениями на действие поперечных сил …..….…….31

4.4. Расчёт изгибаемых элементов по наклонным

сечениями на действие изгибающих моментов….….34

4.5. Конструктивные требования к постановке

поперечной арматуры ……………………...............…37

II. Расчёт и конструирование сжатых элементов.…………………39

1. Классификация сжатых элементов ………………….…….39

2. Основы конструирования сжатых элементов ……...…….41

3. Расчёт элементов сжатых со случайным

эксцентриситетом……………………………..……………….44

4. Расчёт внецентренно сжатых элементов …………………48

4.1. О характере работы и разрушения внецентренно

сжатых элементов …………………………………….48

4.2. Учёт влияния прогиба элемента ……………..………50

4.3. Расчёт сжатых элементов прямоугольного сечения

в случае больших эксцентриситетов …………….………52

Б. Расчёт железобетонных конструкций по второй группе

предельных состояний ………………..……………………….....58

1. Общие положения …………………………………….…..…..58

2. Расчёт железобетонных конструкций

по трещиностойкости ……………….…………………..…….60

2.1. Расчёт по образованию трещин …………….……..……60

2.2. Расчёт по раскрытию трещин ……………………...……62

3. Расчёт железобетонных конструкций по деформациям ……64

3.1. Расчёт по прогибам …………………………………..…..64

3.2. Расчёт углов сдвига элемента ……………………….......68

ЛИТЕРАТУРА ……………………………………………………….69

Date: 2016-02-19; view: 911; Нарушение авторских прав