Теоретические сведения. 1.Векторная диаграмма тока и напряжений

1.Векторная диаграмма тока и напряжений. Если в неразветвлённой цепи с активным сопротивлением R, индуктивностью L и емкостью C (рис. 3) протекает синусоидальный ток i=I_mSINjt, то мгновенное значение приложенного к цепи напряжения u=u_a+u_L+u_c. Напряжение на активном сопротивлении Ua совпадает по фазе с током в цепи I, напряжение на индуктивности U_L опережает ток на 90°, а напряжение на ёмкости U_C отстает от тока на 90.

Рис.3

Действующие значения напряжений на участках цепи: Ua=IR; U_L=IX_L; U_C=IX_C. Действующее значение напряжения на зажимах цепи получим методом векторного сложения: U=Ua+U_L+U_C. Построим векторную диаграмму тока и напряжений. Сначала отложим вектор тока I (рис.4). Вектор падения напряжения в активном сопротивлении Ua совпадает по фазе с вектором тока I, вектор индуктивного падения U_L отложим вверх под углом 90⁰, а вектор емкостного падения напряжения U_C - вниз под углом 90⁰ к вектору тока I. Сложив векторы напряжений Ua, U_L, U_C, получим вектор напряжения U, приложенного ко всей цепи. Векторная диаграмма построена для случая, когда X_L>X_C и цепь имеет активно- индуктивный характер.

Рис.4

При этом условии U_L>U_C, а напряжение U опережает по фазе ток I на угол j. Если X_C>X_L, то U_C>U_L и цепь имеет активно-ёмкостный характер. При этом напряжение U (рис.2) отстаёт по фазе от тока I на уголj. При равенстве реактивных сопротивлений (X_L=X_C) U_L=U_C (рис.5). При этом напряжение U совпадает по фазе с током I (j=0) и цепь носит активный характер.

Рис. 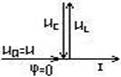5

Этот режим в рассматриваемой цепи называется резонансом напряжений.

2.Треугольники сопротивлений и мощностей. Рассмотрим треугольник напряжений на (рис.6а). Один катет этого треугольника выражает активное напряжение Ua, другой – реактивное напряжение цепи U_L-U_C, а гипотенуза - полное напряжение U. Разделив стороны треугольника напряжений на ток I,получим треугольник сопротивлений (рис.6б), из которого следует, что полное сопротивление цепи равно:

Z=

Поэтому ток в цепи:

I=U/Z=U/

Если все стороны треугольника напряжений (см. рис.6а) умножить на ток I, то получим треугольник мощностей (см. рис.6в).

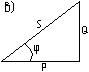Рис.6

Мощности:

Активная:

P=UaI=I²R=UICOSj, где COSj=Ua/U=R/Z;

Реактивная:

Q=(U_L-U_C)*I=I²*(X_L-X_C)=UISINj;

Полная:

S=UI=

Пример 2

Неразветвлённая цепь имеет сопротивления: R=4 Ом; X_L=10Ом и X_C=7Ом. Напряжение на зажимах цепи U=24В. Определить ток, активную, реактивную и полную мощности цепи.

Решение:

Полное сопротивление цепи Z= = =5 Ом.

Полный ток I=U/Z=24/5=4.8 А.

Мощности:

Активная P=I²*R=4.8²*4=92.2 Вт;

Реактивная Q=I²(X_L-X_C)=4.8²(10-7)=69.1 Вар;

Полная S =UI=24*4.8=115.2 ВА.

Задача 3.

К источнику трехфазной сети подключена равномерная нагрузка, соединенная по схеме «звезда», Определить активное сопротивление, активную, реактивную и полную мощности каждой фазы и всей системы, коэффициент мощности, значения линейных и фазных токов и напряжений. Начертить схему цепи. Построить векторную диаграмму линейных и фазных токов и напряжений.

Табл. 3. Расчетные данные для задачи 3

Решение этой задачи требует знания учебного материала темы 1.5, представления об особенностях соединения потребителей в звезду и треугольник, соотношений между линейными и фазными напряжени­ями и токами при таких соединениях, умения строить векторные диаг­раммы. Для пояснения методики решения задач на трехфаз­ные цепи приведён пример 3 с подробным решением.

Методические указания к решению задачи 3:

Date: 2016-02-19; view: 4740; Нарушение авторских прав