Пример 4

Предположим, при исходных данных примера 3, транзитная норма отправки равна 250 единиц продукции, т.е. q_тн =250 ед. Тогда время между двумя смежными заказами будет равно

τ^“_сз = 250 х 52/1200 = 11 недель.

Допустим также, что доставка осуществляется по железной дороге, причем тариф для транзитной нормы ρ_тн — 0,4 ден. ед., а время в пути уменьшается до 1,2 недель.

Тогда затраты будут соответственно равны:

C′_∑ = 60,8 х 1200/151 + 29,3x0,22 х 151/2 + 1,4/6,5 х 29,3 х 0,1 х 151 + 0,6 х 1200 = 1785 ден. ед.

C^”_∑ = 60,8 х 1200/250 + 29,3 х 0,22 х 250/2 + 1,2/11 х 29,3 х 0,1 х 250 + 0,4 х 1200 =1657 ден. ед.

Таким образом оптимальным размером заказа будет заказ q*_TH, соответствующий транзитной норме грузовой отправки, равной 250 единиц.

Похожая на описанную выше ситуация наблюдается при действии оптовых скидок при возрастании объема заказа (поставки) продукции.

Рассмотрим теперь влияние неопределенности параметров на принимаемые логистические решения по управлению запасами, в частности, для EOQ модели.

Классическая EOQ модель является идеализированной схемой, иллюстрирующей процесс управления запасами (оптимизации) при полностью детерминированных параметрах. На практике логистическому менеджеру постоянно приходится сталкиваться с различными ситуациями, вызывающими неопределенность параметров спроса, заказа и поставок. Эта неопределенность объясняется как самой стохастической природой некоторых параметров, например, интенсивности спроса/расхода, так и влиянием различных логистических рисков.

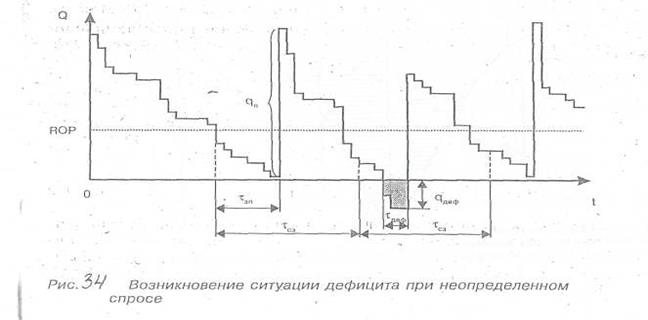
На рис. 34 проиллюстрировано влияние неопределенности спроса (расхода) на параметры управления запасами.

Если предположить, что параметры управления запасами ROP, были определены для классической модели при средней интенсивности спроса λ, а реальный спрос является случайной величиной, распределенной по нормальному закону, то плотность распределения величины ROP будет иметь вид, представленный на рис. 35.

На графике (рис. 35) показано, что разброс возможных значений Q₃ вокруг среднего Q₃ = ROP для нормального распределения с вероятностью у = 0,97 укладывается в диапазон (ROP — 3σ, ROP + 3σ) — по правилу «шесть сигм».

Если предположить далее, что EOQ=q_н и τ_сз остаются постоянными, неопределенность Q₃ может вызвать дефицит (рис. 34), т.е. отсутствие запаса в период τ_деф с максимальной величиной q_деф.

Неопределенность исходных параметров систем управления запасами вызывается также многочисленными логистическими рисками, например, в сроках доставки продукции, объемах поставок, качестве МР и ГП, ассортименте; рисками, связанными со стихийными бедствиями, возможностью хищений, пожаров, естественной убыли и т.п. Связанная с этими причинами неопределенность также может вызвать явление дефицита, аналогично тому как это проиллюстрировано на рис. 34, причем неопределенными (стохастичными) могут быть все параметры модели управления запасами или их отдельные комбинации.

Для элиминирования возможности возникновения дефицита создают страховые (гарантийные) запасы, как это показано на рис. 26 для классической модели. Определение величины Q_стр страхового запаса производится обычно на основе элементарных методов математической статистики. Тогда для модели EOQ величина точки заказа будет равна:

ROP= Q₃ + Q_стр (16)

Наиболее простой способ расчета страхового запаса заключается в расчете доверительного интервала для Q₃ по формуле:

Q₃ = ω х σ _Q3 / √N (17)

где ω — параметр (аргумент) функции Лапласа Ф(ω);

σ _Q3 — С. К.О. точки заказа;

N — количество заказов за год.

Параметр ω определяется по величине доверительной вероятности γ из условия:

2Ф(ω) = γ (18)

Date: 2016-02-19; view: 450; Нарушение авторских прав