Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Показатели тесноты связи
|
|
Теснота корреляционной связи может быть измерена эмпирическим корреляционным отношением hэ, когда d2 (межгрупповая дисперсия) характеризует отклонение групповых средних результативного признака от общей средней: 
.
Говоря о корреляционном отношении как о показателе измерения тесноты зависимости, следует отличать от эмпирического корреляционного отношения – теоретическое.
Теоретическое корреляционное отношение h представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения выравненных значений результативного признака d, т. е. рассчитанных по уравнению регрессии, со средним квадратическим отношением эмпирических (фактических) значений результативного признака s:
h =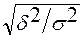 
,
где d2 =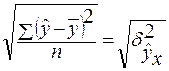 
; s = 
Тогда h = 
.
Изменение значения h объясняется влиянием факторного признака.
В основе расчета корреляционного отношения лежит правило сложения дисперсий 
, где 
- отражает вариацию y за счет всех остальных факторов, кроме x, т. е. является остаточной дисперсией:
.
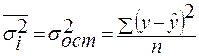Тогда формула теоретического корреляционного отношения примет вид:
или 
.
Подкоренное выражение корреляционного отношения представляет собой коэффициент детерминации.
Корреляционное отношение может находиться в пределах от 0 до 1, т. е.
(0 £ h £ 1) Чем ближе корреляционное отношение к 1, тем связь между признаками теснее.
Теоретическое корреляционное отношение применяется для измерения тесноты связи при линейной и криволинейной зависимостях между результативным и факторным признаком.
Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи – линейный коэффициент корреляции:
где n – число наблюдений.
Для практических вычислений при малом числе наблюдений (n £ 20-30) линейный коэффициент корреляции удобнее исчислять по следующей формуле:
Он принимает значение в интервале: -1 £ r £ 1. Отрицательные значения указывают на обратную связь, положительные - на прямую. При r = 0 линейная связь отсутствует. Чем ближе коэффициент корреляции по абсолютной величине к единице, тем теснее связь между признаками. И, наконец, при r = ± 1 связь – функциональная.
Множественный коэффициент корреляции вычисляется при наличии линейной связи между результативными и несколькими факторными признаками, а также между каждой парой факторных признаков.
Множественный коэффициент корреляции вычисляется по формуле:
, где 
- дисперсия теоретических значений результативного признака, рассчитанная по уравнению множественной регрессии; 
- общая дисперсия результативного признака.
В случае оценки тесноты связи между результативным и двумя факторными признаками множественный коэффициент корреляции можно определить по формуле:
,
где r – парные коэффициенты корреляции между признаками., которые могут быть рассчитаны по следующим формулам:
;
;
.
Date: 2016-02-19; view: 486; Нарушение авторских прав