XXV. Компоновки приводов главного движения для станков нормальной и высокой точности

Приводы главного движения различаются в основном по типу двигателя, компоновке, по способу регулирования и переключения частот вращения. Общая структурная схема привода главного движения представлена на рис. 122. Наличие и вид тех или иных элементов в конкретном приводе в первую очередь определяется технологическим назначением станка, его общей компоновкой и системой управления.

Рис. 122 Общая структурная схема привода главного движения.

Передаточный механизм должен иметь общее передаточное отношение ,

где – передаточные отношения соответствующих устройств передаточного механизма.

Соединение двигателя с коробкой С1 (с передаточным отношением i) выполняется в зависимости от компоновки станка в виде ременной или зубчатой передачи либо соединительной муфты. Коробка скоростей (КС) при нерегулируемом двигателе (М) предназначена для изменения передаточного отношения привода, чтобы получить на шпинделе различные скорости вращения в пределах от п_min до n_max т.е. 12 настраивается в соответствии с режимами резания.

При разделенном приводе шпиндель станка (Ш) располагается в отдельном корпусе шпиндельной бабке (Ш.Б.). В зависимости от требований по плавности вращения шпинделя, а также величины передаваемого момента соединение С2 выполняется в виде ременной или зубчатой передачи с передаточным отношением . Иногда в этом случае в шпиндельной бабке имеются переключаемые зубчатые передачи (перебор) с общим передаточным отношением (рис. 123). Высокие частоты вращения ( = 1) шпиндель получает от коробки скоростей через ременную передачу при включении муфты А влево (при* этом колеса Z2 и Z3 выключаются за счет осевого смещения втулки Б, на которой они закреплены). При выключении муфты и включении зубчатых колес Z2 и Z3 шпиндель получает малые частоты вращения и . Разделенный привод применяется в точных станках небольшого и среднего размера, когда не требуется осевого перемещения шпиндельной бабки.

При неразделенном приводе отсутствует отдельная коробка скоростей, а зубчатые передачи, служащие для изменения общего передаточного отношения, располагаются в шпиндельной бабке (рис. 124, а). В этом случае шпиндельная бабка может называться коробкой скоростей. Коробка скоростей, показанная на рис. 124, в зависимости от положения зубчатых блоков позволяет получить 12 различных частот вращения шпинделя и ее передаточное отношение .

Рис. 123 Схема раздельного привода.

Рис. 124 Привод с коробкой скоростей:

а) кинематическая схема б) график частот вращения.

По сравнению с разделенным привод упрощается, однако ухудшается плавность вращения шпинделя, так как обычно применяется зубчатая (иногда косозубая) передача на шпинделе с передаточным отношением ременную передачу применить сложно. Кроме того, тепло, выделяемое в коробке скоростей, отрицательно сказывается на работе шпиндельного узла.

В качестве источника движения в станках чаще всего применяется электродвигатель, его расположение относительно коробки скоростей определяет тип соединения С1 (см. рис. 122). При ременной передаче двигатель может быть расположен рядом со станком либо на станке в удобном месте. Возможно соединение двигателя с коробкой скоростей с помощью соответствующих муфт либо фланцевая его установка. В отдельных случаях привод выполняется в виде унифицированного узла – электрошпинделя (мотор-шпиндель), ротор электродвигателя, в котором насаживается непосредственно на шпиндель.

XXVI.Графоаналитический расчет коробок скоростей. Граничные условия.

С учетом необходимости получения оптимальных по ре­жимам резания скоростей для различных диаметров обработки при­вод должен обеспечивать любую частоту вращения шпинделя n = (1000v/πD) в пределах выбранного диапазона регулирования R_n, т.е. требуется бесступенчатое регулирование частоты его вращения.

Рис. 125. Диаграмма частоты вращения шпинделя при ступенчатом регулировании

Однако существующие способы бесступенчатого регулирования отличаются повышенной стоимостью, а при использовании механиче­ских вариантов — низкой надежностью и повышенными потерями. Поэтому в настоящее время в станках, особенно общего назначения и без числового управления, пока еще широко применяют при­воды со ступенчатым регулированием с асинхронными нерегулируемыми электродвигателями. Основные их достоинства — небольшая стои­мость, высокий КПД, компактность, жесткость характеристики, возможность получения постоянства мощ­ности на всем диапазоне регулирования. При том про­межуточные значения частот вращения выбирают, как пра­вило, по закону геометриче­ской прогрессии.

Целесооб­разность применения геометрического ряда частот вращения была обоснована акад. А. В. Гадолиным в 1876 г., исходя из обеспечения постоянства потери экономически выгодной скорости для всех интервалов ряда, что обеспечивает по­стоянство потери технологической производительности при прочих равных условиях обработки.

В координатах V и D (рис. 125) геометрический ряд с частотами

n₁=n_min,

n₂=n_min,

n₃=n₂φ=n₁φ²,

………………..

n_k=n_k-1 φ=n₁ φ^k-1,

………………..

n_z=n₁ φ ^z-1=n_max, (52)

где z – число ступеней скорости, а φ = const – знаменатель ряда частот вращения, представляется в виде совокупности прямых линий , проходящих через начало координат.

Следовательно, при обработке заготовки размером D₀ может воз­никнуть потеря экономически выгодной скорости ∆V, которая будет наибольшей, если выбранная скорость v→v_k+1 не может быть пре­вышена исходя из условий резания (например, по условию обеспе­чения требуемой стойкости инструмента). При этом ∆v_max=v_k+1 – v_k, а наибольшая относительная потеря скорости и пропорцио­нальная ей потеря производительности

(53)

Для геометрического ряда частот вращения число ступеней z скорости может быть определено из соотношения

(54)

Отсюда

(55)

Вычисленную по этой формуле величину z округляют до целого, не всегда ближайшего числа, что приводит к некоторому изменению действительного диапазона регулирования R_n. Геометрический ряд частот вращения шпинделя обладает и структурными преимуще­ствами. Ступенчатое регулирование целесообразно осуществлять по­следовательно включенными группами зубчатых передач в виде двойных и тройных блоков; при этом из закономерных рядов ча­стот вращения шпинделя можно осуществить только геометриче­ский ряд.

φ	Е1	Е2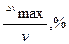
1,06
1,12
1,26
1,41	20/3
1,58		3/2
1,78		6/5
	20/6

Табл. 7 Стандартные значения знаменателя геометрического ряда при заданных значениях числа членов ряда/

В станкостроении все значения знаменателя φ, как и сами ряды частот вращения, стандартизова­ны. При установлении значений φ, которые лежат в пределах 1 φ 2,учитывали стандартные десятичные ряды предпочтительных чисел, т.е. φ = 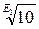, где Е₁ – целое число членов ряда в десятичном интервале, равное 40, 20, 10, 5, 4. Кроме того, для возможности применения двухскоростных электродвигателей с отношением синхронных частот вращения, равным 2, необходимо выдерживать принцип удвоения частот в ряду, т. е. φ = , где E₂ – целое число. Тогда, если в ряду частот есть член п_х, то будет также член п_y = 2п_х = пxφ^E2 т. е. Е₂ – число членов ряда в двоичном интервале.

Стандартные значения знаменателя ряда приведены в табл. 7, там же указаны величины потерь экономически выгодной скорости. Малые значения знаменателя ряда приводят к существенному услож­нению привода, что экономически оправдывает применение систем бесступенчатого регулирования, поэтому φ = 1,06 в станках прак­тически не применяют; φ = 1,12 применяют преимущественно в стан­ках с числовым управлением и в тяжелых станках, где требуется более точная настройка на заданный режим. Наибольшее распространение получили значения φ = 1,25 и φ = 1,4; φ = 1,58 и φ = 1,8 применяют в специализированных станках, где велико вспомогательное время и поэтому точное установление скорости не обя­зательно; φ = 2 практически не применяют, так как потеря произ­водительности в этом случае достигает 50 %.

Для того чтобы кинематическая цепь привода шпинделя обеспе­чивала геометрический ряд частот вращения в расчетном диапазоне R_n c выбранным φ при последовательно включенных между смежными валами групповых передачах (рис. 126), необходимо выполнение ряда закономерностей.

Рис. 126. Привод главного движения при ступенчатом регулировании частот вращения:

а – кинематическая схема; б – варианты структурных сеток; в – график частот вращения

Общее число ступеней скорости

(56)

где p_k –число отдельных передач в каждой группе; т – число групп передач.

Общий диапазон регулирования

(57)

где i_max, i_min — соответственно наибольшее и наименьшее переда­точное отношение привода; , – соответственно наи­большее и наименьшее передаточное отношение в k -й группе передач;

R_k = 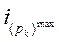/ – диапазон регулирования k -й группы.

Передаточные отношения передач влюбой группе должны стро­иться по закону геометрической прогрессии со знаменателем

φ_k =R_k-1φ =φ^xk, (58)

а именно

(59)

где R_k-i – диапазон регулирования совокупности передач, кинематически включаемых ранее данной группы; x_k – характеристика группы, определяющая ряд передаточных отношений, т.е. порядок ее кинематического включения. Диапазон регулирования группы

(60)

В порядке кинематического включения различают основную груп­пу передач с числом отдельных передач р₀, которая обеспечивает на­чальный ряд частот вращения со знаменателем φ₀ =φ. Для нее характеристика x_k = х₀ = 1, ряд передаточных отношений i₁: i₂: i₃:... = 1: φ: φ²: …, а диапазон регулирования R₀ = φ^(p0-1). Множительные (переборные) группы служат для расширения (раз­множения) начального ряда частот до требуемого диапазона R_n и числа ступеней z.

Первая переборная группа с числом передач р₁ имеет характери­стику x₁ = р_о при φ₁= R₀φ = φ^(p0^-1)φ = φ^р0 и обеспечивает ряд передаточных отношений i₁: i₂: i₃:... = 1: φ^р0: φ^{2 р0}: …, Диа­пазон ее регулирования R₁ = φ₁^(p1-1) = φ^р0(p1-1) .

Вторая переборная группа с числом передач р₂ имеет характери­стику х₂ – p_op₁ и знаменатель ряда передаточных отношений φ₂ = R₀R₁φ = φр_ор₁, обеспечивая ряд передаточных отношений i₁: i₂: i₃:... = 1: φ^р0р1: φ^р0р1: …; диапазон ее регулирования R₂ = φ ^(р2-1) = φ^{р0р1(р2-1)}.

Различные варианты привода для данного числа z, учитывающие порядок конструктивного расположения и кинематического включе­ния групп, удобно характеризовать формулой структуры привода. Она получается, если в формуле (56) записать группы R_k в порядке их конструктивного расположения, а индексы ставить в соответствии с порядком их кинематического включения.

Для облегчения кинематического расчета привода применяют. графоаналитический метод, основанный на последовательном по­строении двух графиков: графика структуры (структурная сетка) и графика частот вращения. Графики строят в логарифмических ко­ординатах с расстоянием (интервалом) между соседними горизон­талями, соответствующими определенным частотам ряда п, равным

lg n_k+1 – lg n_k = lg φ = const. (61)

При этом все передаточные отношения и диапазоны регулирова­ния в приводе, которые представляют собой целые степени знаме­нателя φ, определяются соответствующим количеством этих интер­валов.

Последовательно расположенные валы привода условно изобра­жают вертикальными линиями; лучи, соединяющие точки пересе­чения на вертикалях, соответствуют передаточным отношениям от­дельных передач между соответствующими валами; число лучей, выходящих из одной точки — числу отдельных передач между ва­лами, число точек на линии вала — числу различных ступеней ско­рости на нем.

Структурную сетку строят в соответствии с выбранной форму­лой структуры привода и учитывают только валы групповых пере­дач. В ней находит отражение относительная связь между переда­точными отношениями в группах в соответствии с условием (59), поэтому лучи для каждой группы проводят симметрично, а количе­ство интервалов между их концами численно равно характеристике группы, определяемой в соответствии с формулой структуры. На рис. 126, б приведены теоретически возможные структурные сетки для привода, изображенного на рис. 126, а в соответствии с кон­структивным вариантом z = 3x2x2. Под каждым вариантом записана формула структуры, а над каждым полем, отведенным для соответствующей групповой передачи, записаны число передач и характеристика группы.

Общее число структурных вариантов для определенной конструк­тивной схемы равно числу перестановок из т групп, т. е. m!, но для заданного числа групп m можно построить (m!/q!) различных конструктивных вариантов, где q – число групп с одинаковым числом пере­дач. Следовательно, общее число вариантов структур для привода, содержащего т групп, равно

, (62)

т. е. для привода с z = 12, где т = 3, a q = 2, общее число вариантов равно 18.

График частот вращения (рис. 126, в) строят в соответствии с разработанной с учетом служебного назначения станка кинемати­ческой схемой. Он отражает частоты вращения всех валов привода, включая валы одиночных передач, необходимых для его компоновки. Построение начинают с цепи редукции i_min, обеспечивающей снижение частоты вращения электродвигателя n_э до п₁ = n_min на шпин­деле. Для дальнейшего построения используют структурную сетку. Передаточное отношение передачи определяется выражением φ^k, где k, учитывая логарифмический характер графика, – число ин­тервалов между горизонталями, перекрытых лучами, соединяю­щими отметки частот вращения на соседних валах. Для повышаю­щей передачи k > 0, для понижающей k < 0, для передачи с i = 1, k = 0. При проведении лучей учитывают ограничения по пре­дельно допустимым значениям передаточных отношений для зубча­тых передач. Для прямозубых передач в приводе главного движения обычно принимают

, (63)

. (64)

Эти условия ограничивают допустимый диапазон регулирования групповой передачи, который с учетом соотношения (60) можно записать в виде

. (65)

Последнее соотношение позволяет уже на стадии построения струк­турных сеток отбросить ряд непригодных вариантов. При выборе структуры и при построении графиков частот вращения следует учитывать, что размеры валов и модули зубчатых колес связаны с частотой вращения следующими зависимостями:

(66)

где С₁ и С₂ – соответствующие постоянные.

Поэтому для уменьшения габаритных размеров и массы при­вода желательно, чтобы большее число его элементов работало в об­ласти более высоких частот вращения. Этому соответствуют приводы, у которых число передач в группах уменьшается, а характеристика увеличивается вдоль цепи передач от электродвигателя к шпинделю. Кроме того, рекомендуется цепь редукции i_min строить так, чтобы выполнялось условие

, (67)

Для уменьшения радиальных размеров передач, которые опреде­ляют размеры корпусных деталей привода, лучшим вариантом будет тот, у которого для каждой группы выдерживается соотношение i_max/i_min=1. Для уменьшения числа валов в приводе и зубчатых колес следует уменьшать число групп передач, которое получится минимальным, если

, (68)

При выборе варианта привода необходимо учитывать также его КПД, возникающие при переходных процессах динамические нагрузки, определяемые значением приведенного момента инерции вра­щающихся масс и длиной кинематических цепей. Во многих случаях это вынуждает прибегать к специальным структурам.

Date: 2016-02-19; view: 1709; Нарушение авторских прав