Решение с помощью ППП Excel. Вычисление параметров линейного уравнения множественной регрессии

Вычисление параметров линейного уравнения множественной регрессии.

Эта операция проводится с помощью инструмента анализа данных Регрессия. Она аналогична расчету параметров парной линейной регрессии, а отличие от парной регрессии состоит только в том, что в диалоговом окне при заполнении параметров входной интервал Х следует указывать не один столбец, а все столбцы, содержащие значения факторных признаков. Результаты анализа представлены на рис. 3.1

Рис.3.1. Результат применения инструмента Регрессия

По результатам вычислений составим уравнение множественной регрессии с помощью результатов вычислений в Ecxel [ Коэффициенты ] вида:

;

.

Значения случайных ошибок параметров , и [ Стандартная ошибка ] с учетом округления:

, , .

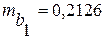Они показывают, какое значение данной характеристики сформировалось под влиянием случайных факторов. Эти значения используются для расчета t-критерия Стьюдента [ t-статистика ]:

; ; ,

Если значения t-критерия больше 2-3, можно сделать вывод о существенности данного параметра, который формируется под воздействием неслучайных причин. Здесь статистически значимыми являются и , а величина сформировалась под воздействием случайных причин, поэтому фактор , силу влияния которого оценивает , можно исключить как несущественно влияющий, неинформативный.

На это же указывает показатель вероятности случайных значений параметров регрессии: если меньше принятого нами уровня (обычно 0,1; 0,05 или 0,01; это соответствует 10%, 5% или 1% вероятности), делают вывод о несущественной природе данного значения параметра, т.е. о том, что он статистически значим и надежен. В противном случае принимается гипотеза о случайной природе значения коэффициентов уровня. Здесь > 5%, что позволяет рассматривать как неинформативный фактор и удалить его для улучшения данного уравнения.

Величина оценивает агрегированное влияние прочих (кроме учтенных в модели факторов и ) факторов на результат y.

Величины и указывают, что с увеличением и на единицу конечный результат увеличивается соответственно на 0,9459 и 0,0856 млн. руб. [ Коэффициенты ]. Сравнивать эти значения не следует, т.к. они зависят от единиц измерения каждого признака и потому несопоставимы между собой.

4. Оценку надежности уравнения регрессии в целом и показателя тесноты связи 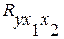дает F-критерий Фишера:

По данным таблицы дисперсионного анализа, представленной на рис. 3.1 =151,65. Вероятность случайно получить такое значение F-критерия составляет 0,0000, что не превышает допустимый уровень значимости 5%; об этом свидетельствует величина Р-значения из этой же таблицы. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи .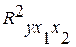

Значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации приведены на рис. 3.1 в рамках регрессионной статистики.

Нескорректированный коэффициент множественной детерминации [ R-квадрат ] 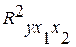=0,9469 оценивают долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 94,7% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом.

Скорректированный коэффициент множественной детерминации [ Нормированный R-квадрат ] 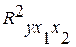=0,9407 определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и потому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более 90%) детерминированность результата y в модели факторами и .

5. Информация для оценки с помощью частных F- критериев Фишера целесообразности включения в модель фактора после фактора и фактора после фактора может быть получена в ППП Statgraphics. Частный F- критерий показывает статистическую значимость включения фактора после того, как в нее включен фактор .

Но по данным, вычисленным с помощью ППП Excel, можно сделать общий вывод, который состоит в том, что множественная модель с факторами и с 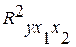=0,9469 содержит неинформативный фактор . Если исключить фактор , то можно ограничиться уравнением парной регрессии:

более простым, хорошо детерминированным, пригодным для анализа и для прогноза.

6. Средние частные коэффициенты эластичности показывают, на сколько процентов от значения своей средней изменяется результат при изменении фактора 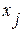на 1% от своей средней и при фиксированном воздействии на у всех прочих факторов, включенных в уравнение регрессии. Для линейной зависимости

,

где - коэффициент регрессии при 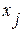в уравнении множественной регрессии.

Здесь ,

.

По значениям частных коэффициентов эластичности можно сделать вывод о более сильном влиянии на результат у признака фактора , чем признака фактора : 0,6% против 0,2%.

Date: 2016-02-19; view: 555; Нарушение авторских прав