Связь между вписанным и центральным углом

Задание № 9.

Окружность

Серединный перпендикуляр

рис 1 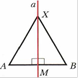рис 2

Определение: Серединный перпендикуляр отрезка является геометрическим местом точек (ГМТ), равноудалённых от концов этого отрезка.

Свойство1: Каждая точка серединного перпендикуляра равноудалена от концов этого отрезка (рис 2).

Дуга окружности, центральные и впи­сан­ные углы.

Теория

Определение: Окружностью называется геометрическое место точек равноудаленных от заданной точки.(вопр. 3,4 495, 497, 500,493)

C = 2

Формула длины окружности

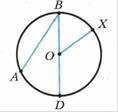
О – центр окружности, АВ – хорда, XD – дуга окружности, ВD = D – диаметр, ОХ = OB = OD = R – радиусы.

Свойство 1: Диаметр окружности, делящий хорду, отличную от диаметра, пополам, перпендикулярен этой хорде.

Свойство 2: Все диаметры окружности равны

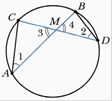
Свойство пересекающихся хорд. Если хорды АВ и СD окружности пересекаются в точке М, то и АМ·МВ = DМ·МС.

Определение: вписанным углом окружности называется угол, вершина которого лежит на окружности, а стороны пересекают окружность.

Свойство 1: градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.

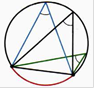
Свойство 2: Вписанные углы, опирающиеся на одну и ту же дугу равны.

Свойство 3: Вписанный угол, опирающийся на диаметр прямой (90°).

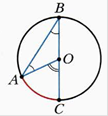
Определение: центральным углом окружности называется угол с вершиной в центре окружности.

Теорема: Центральный угол равен величине дуги, на которую он опирается.

Свойство: Центральный угол, опирающийся на хорду равную радиусу этой окружности равен 60°.

Связь между вписанным и центральным углом.

Теорема: Центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу окружности. (<АОС = 2∙ <АВО).

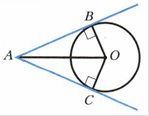
Определение: Прямую, имеющую с окружностью только одну общую точку, называют касательной к окружности.

Теорема: Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

Свойство угла между касательной и хордой <М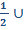АВ = АВ

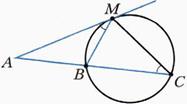Свойство касательной к и секущей АМ² = АС∙АВ.