
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические указания. Исследование арифметического сумматора
|
|
Задание №8
Исследование арифметического сумматора
Цель работы: исследовать арифметический сумматор,
полусумматор и полный сумматор.
| Вариант | Номера наборов | Вариант | Номера наборов |
| A+2= 8+7= 3+B= | 6+6= E+4= 2+B= | ||
| C+3= 6+4= 2+D= | 7+5= C+E= 8+B= | ||
| F+4= 3+6= D+2= | 4+9= F+4= 7+B= | ||
| 1+A= 4+8= E+2= | 5+E= 4+8= C+7= | ||
| 4+E= 6+2= F+D= | B+6= 5+6= A+E= | ||
| 3+7= A+5= 4+E= | 8+2= F+A= B+6= |
Методические указания.
Арифметические сумматоры – составная часть арифметико-логических устройств (АЛУ) микропроцессоров (МП). Арифметический сумматор состоит из двух устройств: полусумматора и n полных сумматоров. Полный сумматор имеет три входа: A, B – входы суммируемых операндов, Ci – вход переноса из предыдущего разряда сумматора и два выхода: S – выход полного сумматора и C 0 – выход переноса. Полусумматор отличается от полного тем, что у него нет входа переноса из предыдущего разряда. Полусумматор используется в качестве первого разряда арифметического сумматора, а в качестве остальных разрядов – полные сумматоры (рис. 1). Полусумматор – одна из простейших комбинационных логических схем.
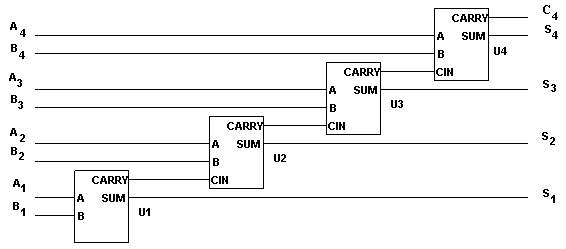
Рис. 1. Четырехразрядный арифметический сумматор
Рассматривая таблицу истинности полусумматора (табл. 2) можно заметить, что выход S полусумматора выполняет функции элемента «ИСКЛЮЧАЮЩЕЕ ИЛИ», а выход переноса С полусумматора – элемента «И». Таким образом, логические выражения для функций S и C равны:
S=AB ′ +A ′ B, C=AB.
Т а б л и ц а 2
| Входы | Выходы | ||
| А | В | S | C |
Схема полусумматора представлена на рис. 2.
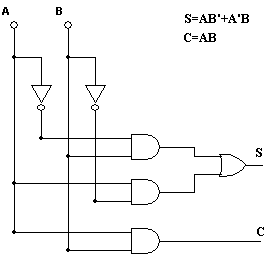
Рис. 2. Структура полусумматора
Из таблицы истинности полного сумматора (табл. 3) можно получить логические выражения для S (суммы) и C (переноса в следующий разряд). Логическое выражение для S будет иметь четыре слагаемых, соответствующих строкам таблицы, в которых выход S равен единице (стоки 4, 5, 7, 10),
S= A ′ B ′ Ci- 1 +A′BCi- 1′ +AB ′ Ci- 1′ +ABCi- 1.
Т а б л и ц а 3
| Входы | Выходы | |||
| А | В | Ci-1 | S | Ci |
Логическое выражение для C также будет иметь четыре слагаемых (строки 6, 8, 9, 10):
Ci=A ′ BCi- 1 +A ′ BCi- 1′ +ABCi- 1′ +ABCi- 1.
С помощью законов булевой алгебры (см. лаб. раб. №1) это выражение можно упростить, тогда оно будет иметь вид
Сi=ACi- 1 +BCi- 1 +AB.
Схема полного сумматора изображена на рис. 3.
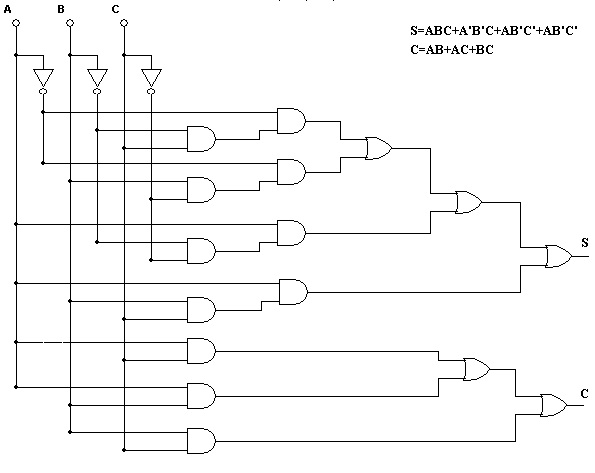
Рис. 3. Структура полного сумматора.
Date: 2016-02-19; view: 765; Нарушение авторских прав