
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Момент импульса. Закон сохранения момента импульса. Моментом импульса материальной точки А относительно неподвижной точки О называется физическая величина
|
|
 Моментом импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением
Моментом импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением
 ;
;
Модуль момента импульса:
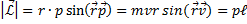
 - радиус-вектор, проведённый из точки O в точку А,? - плечо импульса (кратчайшее расстояние от точки О до линии действия импульса)
- радиус-вектор, проведённый из точки O в точку А,? - плечо импульса (кратчайшее расстояние от точки О до линии действия импульса)
 - импульс материальной точки.
- импульс материальной точки.
 - псевдовектор, его направление определяется по правилу левой руки.
- псевдовектор, его направление определяется по правилу левой руки.
Моментом импульса твердого тела относительно неподвижной оси Z называется скалярная величина равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса 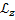 не зависит от положения точки O на оси Z.
не зависит от положения точки O на оси Z.
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:
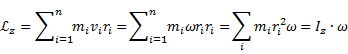
Продифференцируем по dt 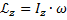
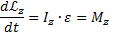
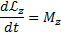
- основное уравнение динамики вращательного движения.
Вообще выполняется векторное равенство
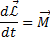
В замкнутой системе момент внешних сил равен нулю
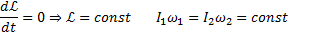
Закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени
§5 Величины, характеризующие поступательное и вращательное движение и связь между ними:
| Поступательное движение | Вращательное движение | Связь | |
 - путь - путь
| 
| 
| |
 - cкорость; - cкорость;

|  
| 
| |
 - ускорение; - ускорение; 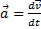
| 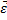 – угловое ускорение – угловое ускорение
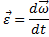
| 
| |
| m - масса | 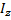 - момент инерции - момент инерции
| 
| |
 - uмпульс; - uмпульс;
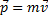
| 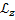 – момент импульса – момент импульса
| 
| |
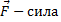 ; ;

| 
| 
| |
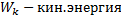 ; ;

|  – кин. энергия вращательного движения – кин. энергия вращательного движения

| ||
d A -элементарная работа;

| d A - элементарная работа вращательного движения 
|
§2 Пружинный маятник.
Упругие и квазиупругие силы.
Уравнение колеблющейся пружины
 Рассмотрим тело массы m, закрепленное на пружине с коэффициентом жесткости k (массой пружины пренебрегаем). Растянем пружину на х. Тогда по закону Гука на тело будет действовать сила упругости F упр:
1) величина силы пропорциональна величине отклонения системы от положения равновесия Рассмотрим тело массы m, закрепленное на пружине с коэффициентом жесткости k (массой пружины пренебрегаем). Растянем пружину на х. Тогда по закону Гука на тело будет действовать сила упругости F упр:
1) величина силы пропорциональна величине отклонения системы от положения равновесия
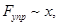 2) направление сила противоположно направлении смещения, т.е. сила всегда направлена к положению равновесия (при х > 0, F упр < 0, при х < 0, F упр > 0)
3) В положении равновесия х = 0 и F упр = 0.
По закону Гука
F упр = - kх.
Систему, состоящую из материальной точки массы m и абсолютно упругой пружины с коэффициентом жесткости k, в которой возможны свободные колебания, называютпружинным маятником.
Запишем второй закон Ньютона для рис. б
2) направление сила противоположно направлении смещения, т.е. сила всегда направлена к положению равновесия (при х > 0, F упр < 0, при х < 0, F упр > 0)
3) В положении равновесия х = 0 и F упр = 0.
По закону Гука
F упр = - kх.
Систему, состоящую из материальной точки массы m и абсолютно упругой пружины с коэффициентом жесткости k, в которой возможны свободные колебания, называютпружинным маятником.
Запишем второй закон Ньютона для рис. б


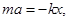

 т.е.
т.е.
 тогда
тогда
 и
и
 Если сила не является по своей природе упругой, но подчиняется закону F = - kх, то она называется квазиупругой силой.
Получим уравнение пружинного маятника. Учтем в записи второго закона Ньютона, что
Если сила не является по своей природе упругой, но подчиняется закону F = - kх, то она называется квазиупругой силой.
Получим уравнение пружинного маятника. Учтем в записи второго закона Ньютона, что
 тогда
тогда
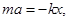


 - дифференциальное уравнение точки, совершающей колебательное движение (дифференциальное уравнение пружинного маятника).
Решение дифференциального уравнения:
- дифференциальное уравнение точки, совершающей колебательное движение (дифференциальное уравнение пружинного маятника).
Решение дифференциального уравнения:
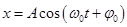 - уравнение колеблющейся точки (уравнение колеблющейся пружины).
- уравнение колеблющейся точки (уравнение колеблющейся пружины).
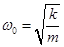 - собственная частота колебаний.
§3 Математический и физический маятники.
Периоды колебаний математического и физического маятников
Математический маятник - материальная точка, подвешенная на невесомой нерастяжимой нити, и совершавшая колебания в вертикальной плоскости под действием силы тяжести. Материальная точка - тело, масса которого сосредоточена в центре масс и размерами которого в условиях данной задачи, можно пренебречь.
- собственная частота колебаний.
§3 Математический и физический маятники.
Периоды колебаний математического и физического маятников
Математический маятник - материальная точка, подвешенная на невесомой нерастяжимой нити, и совершавшая колебания в вертикальной плоскости под действием силы тяжести. Материальная точка - тело, масса которого сосредоточена в центре масс и размерами которого в условиях данной задачи, можно пренебречь.
 Математический маятник при колебаниях совершает движение по дуге окружности радиуса Математический маятник при колебаниях совершает движение по дуге окружности радиуса 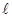 . Его движение подчиняется законам вращательного движения.
Основное уравнение вращательного цветения запишется в виде . Его движение подчиняется законам вращательного движения.
Основное уравнение вращательного цветения запишется в виде
 (1)
М – момент сил, I – момент инерции, ε – угловое ускорение. (1)
М – момент сил, I – момент инерции, ε – угловое ускорение.


 Равнодействующая сил
Равнодействующая сил  и и  равна равна  .
Из треугольника АВС .
Из треугольника АВС
 т.е.
т.е.
 таким образом, колебания математического маятника происходят под действием квазиупругой силы - силы тяжести.
Тогда (1) запишется в виде
таким образом, колебания математического маятника происходят под действием квазиупругой силы - силы тяжести.
Тогда (1) запишется в виде
 (2)
Знак минус учитывает, что векторы (2)
Знак минус учитывает, что векторы  и и  имеют противоположные направления (угол поворота можно рассматривать, как псевдовектор углового смещения имеют противоположные направления (угол поворота можно рассматривать, как псевдовектор углового смещения  , направление вектора , направление вектора  определяется по правилу правого винта, из-за знака минус определяется по правилу правого винта, из-за знака минус  направлен в противоположную сторону).
Сократив в (2) на m и направлен в противоположную сторону).
Сократив в (2) на m и 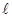 получим получим
 При малых углах колебаний α = 5 ÷6°,
При малых углах колебаний α = 5 ÷6°,  , получим , получим
 Ввода обозначения
Ввода обозначения
 получим дифференциальное уравнение колебаний математического маятника
получим дифференциальное уравнение колебаний математического маятника
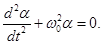 Его решение:
Его решение:
 - уравнение математического маятника.
из которого видно, что угол α изменяется по закону косинуса. α0 - амплитуда, ω0 - циклическая частота, φ0 - начальная фаза.
- уравнение математического маятника.
из которого видно, что угол α изменяется по закону косинуса. α0 - амплитуда, ω0 - циклическая частота, φ0 - начальная фаза.
 - период колебаний математического маятника
Физический маятник - твердое тело, колеблющееся под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через центр тяжести тела, называемой осью качания маятника.
- период колебаний математического маятника
Физический маятник - твердое тело, колеблющееся под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через центр тяжести тела, называемой осью качания маятника.
 Основное уравнение – вращательного движения для физического маятника запишется в виде Основное уравнение – вращательного движения для физического маятника запишется в виде
 При малых углах колебаний
При малых углах колебаний  и уравнение движения имеет вид и уравнение движения имеет вид
 Тогда положив
Тогда положив
 получим
получим
 - дифференциальное уравнение физического маятника.
- дифференциальное уравнение физического маятника.
 - период колебаний физического маятника
Приравняв Тфиз = Тмат:
- период колебаний физического маятника
Приравняв Тфиз = Тмат:
 следовательно, математический маятник с длиной
следовательно, математический маятник с длиной
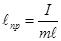 имеет такой же период колебаний, как и данный физический маятник.
имеет такой же период колебаний, как и данный физический маятник.  - приведенная длина физического маятника - это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. - приведенная длина физического маятника - это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.
| |
Вернемся к формулам для смещения x, скорости v и ускорения a гармонического колебательного процесса.
Пусть имеем тело массы «m», которое совершает под действием квазиупругой силы колебания по закону:
 , тогда
, тогда
 .
.
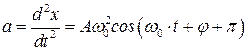 .
.
Видно, что скорость и ускорение также изменяются по гармоническому закону (графики приводились ранее) с периодом колебаний равным T. Из сравнения формул видно, что скорости v опережает смещение по фазе на  . Это означает, что если x=0, то v тела имеет максимальное значение
. Это означает, что если x=0, то v тела имеет максимальное значение  .
.
Для ускорения зависимость иная. В каждый момент времени ускорение пропорционально смещению и находится с ним в противофазе. Это означает, что когда x=xmax, то ускорение тоже максимально, но отрицательно, т.е. при x=xmax,  (графики приведены ранее).
(графики приведены ранее).
Квазиупругая сила, под действием которой происходит колебательное движение, является консервативной. Поэтому полная энергия гармонического колебательного движения должна оставаться постоянной. В процессе колебаний происходит превращение кинетической энергии в потенциальную и обратно (силами сопротивления пренебрегаем). Причем в моменты наибольшего отклонения о положения равновесия  , причем
, причем  ; при прохождении положения равновесия
; при прохождении положения равновесия  , причем
, причем  . Так как
. Так как  , то
, то  .
.
Определим, как со временем изменяется Ек и Uп для гармонического колебания  . Имеем
. Имеем
 (8.4)
(8.4)
 (8.5)
(8.5)
Т.к.  , то имеем
, то имеем
 ,
,
т.е. 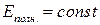 как и должно было быть, т.к. квазиупругая сила – консервативная сила.
как и должно было быть, т.к. квазиупругая сила – консервативная сила.
Используя формулы тригонометрии, можно получить выражения для

 (8.6)
(8.6)
 (8.7)
(8.7)
Здесь E – полная энергия системы. Из формул видно, что Ек и Uп изменяются с частотой 2w0, т.е. с частотой вдвое превышающей частоту гармонического колебания. Среднее значение квадрата sin и квадрата cos равно 1/2. Следовательно, среднее значение Eк совпадает со средним значением Uп и равно E/2.
Date: 2016-02-19; view: 2524; Нарушение авторских прав