Напряжения

Согласно гипотезе сплошности, можно предположить, что внутренние силы непрерывно распределены по площади поперечного сечения бруса. Разделив площадь сечения тела на большое число малых площадок, рассмотрим одну из элементарных площадок ∆А. Как бы ни были размеры этой площадки, на неё будут действовать внутренние силы, распределённые по всему сечению. Мерой интенсивности внутренних сил, распределённых по сечениям, служат напряжения – усилия, приходящиеся на единицу площади сечения.

Пусть ∆R - равнодействующая внутренних сил, действующая на площадку 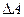(рис. 1.6,а).Тогда среднее значение интенсивности внутренних сил, приходящихся на единицу площади 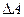будет равно:

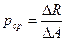
(1.5)

Уменьшая площадь 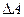до нуля, т.е переходя к пределу получим истинное напряжение в данной точке сечения:

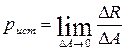
(1.6)

Векторная величина 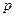называется полным напряжением в точке. В международной системе единиц (СИ) за единицу напряжения принят паскаль (Па) – это напряжение, при котором на площадке 1 м² действует внутренняя сила 1 Н.

Так как эта единица очень мала, в расчетах используют кратную единицу напряжения – мегапаскаль (1 МПа=10⁶ Па=Н/мм²).

Поскольку через точку тела можно провести бесчисленное множество сечений, то в данной точке имеется бесчисленное множество напряжений, связанных с площадками действия. Следовательно, совокупность всех напряжений, действующих на разных площадках в данной точке, называется напряжённым состоянием точки.

Разложим вектор полного напряжения 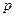на две составляющие (рис.1.6, б).

Проекция вектора полного напряжения 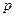на нормаль к данной площадке обознача­ется через 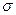и называется нормальным напряжением.

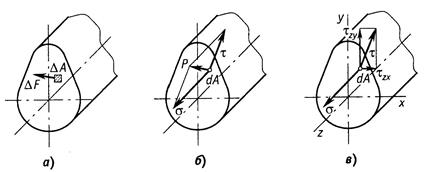
Рис. 1.6

Составляющую, лежащую в сечении в данной площадке обознача­ется через 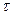и называется касательным напряжением.

Нормальное напряжение, направленное от сечения, считают положительным, направленное к сечению – отрицательным.

Нормальные напряжения возникают, когда под действием внешних сил частицы, расположенные по обе стороны от сечения, стремятся удалиться одна от другой или сблизиться. Касательные напряжения возникают, когда частицы стремятся сдвинуться одна относительно другой в плоскости сечения.

Касательное напряжение можно разложить по координатным осям на две составляющие и 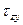(рис.1.6, в). Первый индекс при 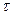показывает, какой оси параллельна нормаль, второй – параллельно какой оси действует напряжение. Если в расчетах направление касательного напряжения не имеет значения, его обозначают без индексов.

Между полным напряжением и его составляющими существует зависимость

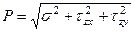(1.7)

Через точку тела можно провести бесконечное число сечений и для каждого из них напряжения имеют свое значение. Следовательно, при определении напряжений необходимо указывать положение не только точки тела, но и сечения, проведенного через эту точку.

Совокуп­ность напряжений для множества площадок, проходящих через данную точку, образует напряженное состояние в этой точке.

Напряжения в поперечных сечениях связаны с внутренними силовыми факторами определенными зависимостями.

Возьмем в сечении бесконечно малую площадку площадью 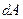. По этой площадке в общем случае действуют бесконечно малые (элементарные) внутренние силы (рис. 1.7)

; ; .

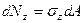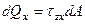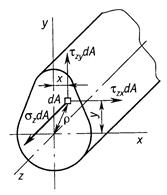
Рис.1.7

Соответствующие элементарные моменты относительно координатных осей , , 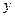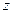имеют вид:

; ; .

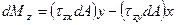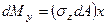Просуммировав бесконечно малые силы и моменты, действующие в сечении, получим выражения, связывающие внутренние силовые факторы с напряжениями:

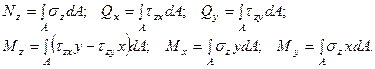(1.8)

В соответствии с теоремой Вариньона, известной из теоретической механики, и зависимостью между напряжениям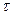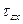и , и 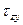, выражение для 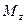можно записать в виде

,

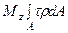где

.

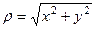Интегральные зависимости (1.8) можно использовать для определения напряжений по найденным методом сечений внутренним силовым факторам при условии, что известны законы распределения напряжений по сечению.

Date: 2015-06-06; view: 496; Нарушение авторских прав